线性代数之——向量空间

1. 向量空间和子空间

向量空间 $R^n$Rn 由所有的 $n$n 维向量 $v$v 组成，向量中的每个元素都是实数。

向量空间 $R^2$R2 可以用 $xy$xy 平面来表示，其中的每个向量有两个元素，它们定义了平面上一个点的坐标。

在一个向量空间中，如果我们将任意向量相加或者乘以一个标量，也就是任意向量的线性组合，它们的结果仍然在这个向量空间中。

三维空间中过原点的一个平面是一个向量空间，这个向量空间和 $R^2$R2 很像，但其中的每个向量都有三个元素。如果我们对这个平面中的两个向量相加，那结果仍然在这个平面中。如果我们对其中的一个向量乘以一个常数，结果也仍然在这个平面中。这个平面位于 $R^3$R3 向量空间里，称为 $R^3$R3 的子空间。

一个向量空间的子空间是由一系列包含零向量的向量组成的，并且满足：如果是 $v$v 和 $w$w 是子空间的两个向量并且 $c$c 是任意标量，那么有 (1) $v+w$v+w在子空间中， (2) $cv$cv 在子空间中。

也就是说，所有向量的线性组合都仍然在这个子空间中。

$R^3$R3 的所有可能子空间有：

• $L$L 所有过 (0, 0, 0) 的直线
• $P$P 所有过 (0, 0, 0) 的平面
• $Z$Z 只有零向量 (0, 0, 0)
• $R^3$R3 整个空间

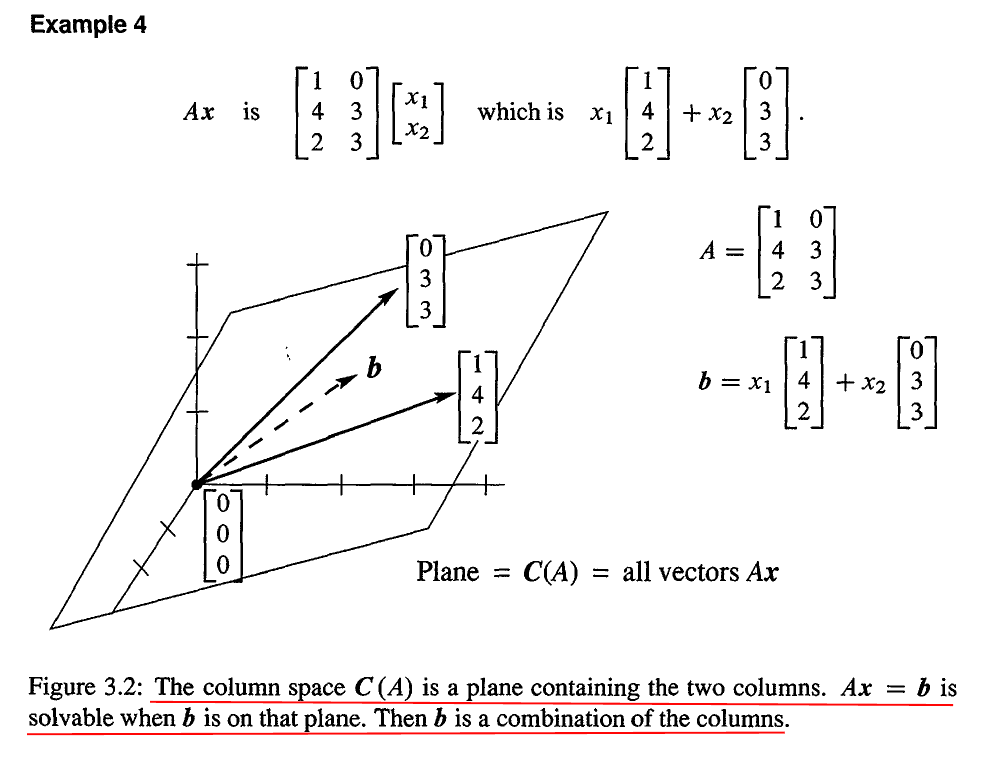
一个最重要的子空间是和矩阵 $A$A 紧密联系的。当我们求解 $Ax=b$Ax=b 时， $Ax$Ax 是对 $A$A 的列的线性组合。为了得到 $b$b，我们用任何可能的 $x$x 来求取 $A$A 的列的所有可能的线性组合，这产生了一个 $A$A 的列空间 $C\left(A\right)$C(A)。 $C\left(A\right)$C(A) 不仅仅包含 $A$A 的所有列向量，还包括他们的所有线性组合。

因此，当我们求解 $Ax=b$Ax=b 时，如果 $b$b 存在于 $A$A 的列空间中的话，我们就可以找到一组系数，使得它们对 $A$A 的列的线性组合就是 $b$b，否则，方程就无解。

2. $A$A 的零空间

矩阵 $A$A 的零空间包含所有 $Ax=0$Ax=0 的解，这些向量位于 $R^n$Rn 中，表示为 $N\left(A\right)$N(A)。

假设 $x$x 和 $y$y 位于矩阵 $A$A 的零空间中，也就是 $Ax=0$Ax=0、 $Ay=0$Ay=0，那就有 $A(x+y)=0$A(x+y)=0、 $A\left(cx\right)=0$A(cx)=0，即它们相加或者乘以一个标量后仍然在零空间中，因此零空间是一个子空间。

零空间是所有特解的线性组合。

平面 $x+2y+3z=0$x+2y+3z=0 可以表示为

$\left[\begin{array}{ccc}1& 2& 3\end{array}\right]\left[\begin{array}{c}x\\ y\\ z\end{array}\right]=0$[1​2​3​]⎣⎡​xyz​⎦⎤​=0

上述方程的两个特解分别为

$s_1=\left[\begin{array}{c}-2\\ 1\\ 0\end{array}\right]，s_2=\left[\begin{array}{c}-3\\ 0\\ 1\end{array}\right]$s1​=⎣⎡​−210​⎦⎤​，s2​=⎣⎡​−301​⎦⎤​

向量 $s_1$s1​ 和 $s_2$s2​ 位于平面 $x+2y+3z=0$x+2y+3z=0 中，这个平面就是矩阵 $A=\left[\begin{array}{ccc}1& 2& 3\end{array}\right]$A=[1​2​3​] 的零空间，这个平面上的所有向量都是 $s_1$s1​ 和 $s_2$s2​ 的线性组合。

注意到，上述特解的最后两个元素分别为 0 和 1，这些元素是自由的并且是我们特殊选择的。因为矩阵 $A=\left[\begin{array}{ccc}1& 2& 3\end{array}\right]$A=[1​2​3​] 的第一列包含一个主元，因此特解的第一个元素是不自由的，自由的元素就对应着该列没有主元。

3. 消元法求解 $Ax=0$Ax=0

这时候，矩阵 $A$A 是矩形的，我们求解有 $n$n 个未知数的 $m$m 个方程。

$A=\left[\begin{array}{cccc}1& 1& 2& 3\\ 2& 2& 8& 10\\ 3& 3& 10& 13\end{array}\right]$A=⎣⎡​123​123​2810​31013​⎦⎤​

第一个主元是 1，然后我们需要将主元下面的 2 和 3 变成 0。

$A\to \left[\begin{array}{cccc}1& 1& 2& 3\\ 0& \boxed{{\displaystyle 0}}& 4& 4\\ 0& 0& 4& 4\end{array}\right]$A→⎣⎡​100​10​0​244​344​⎦⎤​

这时候，第二列主元的位置为 0，并且其下面的位置也为 0，因此我们也无法用行交换来得到一个主元。

这意味着我们遇到了问题，但我们不应该停止，我们继续看第三列。我们得到了第二个主元 4，然后继续向下消元得到下三角矩阵 $U$U。

$U=\left[\begin{array}{cccc}\boxed{{\displaystyle 1}}& 1& 2& 3\\ 0& 0& \boxed{{\displaystyle 4}}& 4\\ 0& 0& 0& 0\end{array}\right]$U=⎣⎡​1​00​100​24​0​340​⎦⎤​

由于第 1 列和第 3 列包含主元，因此主变量就是 $x_1$x1​ 和 $x_3$x3​，而 $x_2$x2​ 和 $x_4$x4​ 是自由变量。

这时候，我们分别将两个自由变量设为 0 和 1，就可以得到方程的解为

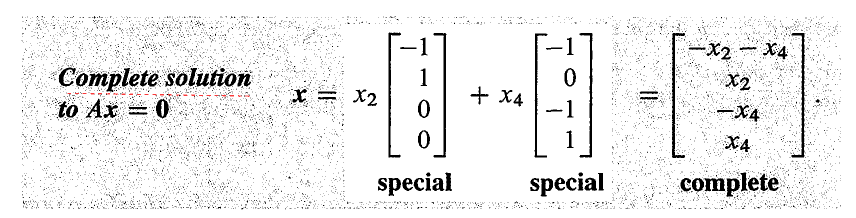
针对每个自由变量都有一个与之对应的特解，所有特解的线性组合就是零空间 $N\left(A\right)$N(A)。如果没有一个变量是自由的，这就意味着方程组只有一个零向量解。

若是 $n\>m$n>m，即列数大于行数，那肯定至少有一个变量是自由的，因为每一行最多只有一个主元，这也就意味着方程组有至少一个特解，这个解是非零的。

对上面的下三角矩阵 $U$U 继续进行消元，第二行除以 4，然后第一行减去第二行的 2 倍，我们可以得到简化行阶梯形式 $R$R

$R=\left[\begin{array}{cccc}1& 1& 0& 1\\ 0& 0& 1& 1\\ 0& 0& 0& 0\end{array}\right]$R=⎣⎡​100​100​010​110​⎦⎤​

这时候，特解就可以很容易地从 $R$R 中读出来，第一个特解的 -1 和 0 就是 $R$R 中第二列的元素 1 和 0 取负号，第二个特解的 -1 和 1 就是 $R$R 中第四列的元素 1 和 1 取负号。

另外，在 $R$R 的左边乘以任意可逆的矩阵，不会改变其零空间。

获取更多精彩，请关注「seniusen」!