PS
这篇文章似乎写歪了啊,因为我测试SSE优化的代码,发现和原始版本的C代码速度是一致?不知道是有什么核心的地方没注意到?我再研究研究吧。
前言
本算法的原理以及优化过程都是偷师ImageShop,也可以把这篇文章理解为https://www.cnblogs.com/Imageshop/p/6376028.html 这篇文章的一篇阅读总结。
原理
首先,高斯滤波是可以用递归算法来实现的。这最早见于《Recursive implementation of the Gaussian filter》论文中:
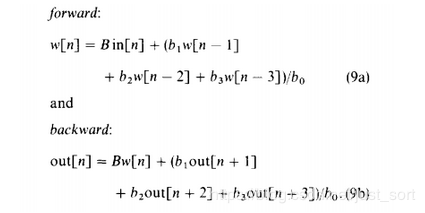
w[n]=Bw[n]+(b1w[n−1]+b2w[n−2]+b3w[n−3])/b0-------(1a)。
同理backward过程中n是递减的,因此在backward前将w的数据完整的拷贝到out中,则式9b则变为:
out[n]=Bout[n]+(b1out[n+1]+b2out[n+2]+b3out[n+3])/b0 -------(1b)。
从编程实现来看,这个拷贝是没有必要的,所以1b可以写成:
w[n]=Bw[n]+(b1w[n+1]+b2w[n+2]+b3w[n+3])/b0------(1c)。
从速度上看,最好是能够去掉1a和1b的除法,所以这里重新定义b1 = b1 / b0, b2 = b2 / b0, b3 = b3 / b0, 最终得到我们使用的递归公式:
w[n]=Bw[n]+b1w[n−1]+b2w[n−2]+b3w[n−3]---------> (a)
w[n]=Bw[n]+b1w[n+1]+b2w[n+2]+b3w[n+3] <---------(b)
这个递推公式的意义就是通过forward和backward来完成一维的高斯滤波。而二维的高斯滤波就是先行后列或者先列后行进行一维的高斯滤波。
算法步骤
- CalGaussCof 计算高斯模糊中使用到的系数
- ConvertBGR8U2BGRAF 将字节数据转换为浮点数据
- GaussBlurFromLeftToRight 水平方向的前向传播
- GaussBlurFromRightToLeft 水平方向的反向传播
- GaussBlurFromTopToBottom 竖直方向的前向传播
- GaussBlurFromBottomToTop 竖直方向的反向传播
- ConvertBGRAF2BGR8U 将结果转换为字节数据
代码实现步骤
对于每一个函数,我都会给出相应的代码实现和我的一些想法,总结,ImageShop博主只给了一部分实现,我依靠自己的理解把某些函数补全了。
CalGaussCof 计算高斯模糊中使用到的系数
void CalcGaussCof(float Radius, float &B0, float &B1, float &B2, float &B3)
{
float Q, B;
if (Radius >= 2.5)
Q = (double)(0.98711 * Radius - 0.96330); // 对应论文公式11b
else if ((Radius >= 0.5) && (Radius < 2.5))
Q = (double)(3.97156 - 4.14554 * sqrt(1 - 0.26891 * Radius));
else
Q = (double)0.1147705018520355224609375;
B = 1.57825 + 2.44413 * Q + 1.4281 * Q * Q + 0.422205 * Q * Q * Q; // 对应论文公式8c
B1 = 2.44413 * Q + 2.85619 * Q * Q + 1.26661 * Q * Q * Q;
B2 = -1.4281 * Q * Q - 1.26661 * Q * Q * Q;
B3 = 0.422205 * Q * Q * Q;
B0 = 1.0 - (B1 + B2 + B3) / B;
B1 = B1 / B;
B2 = B2 / B;
B3 = B3 / B;
}
这个公式是论文原文给出的,然后计算过程可以理解为O(1)的,没有优化空间,也没有对应的SSE优化。
ConvertBGR8U2BGRAF 将字节数据转换为浮点数据
void ConvertBGR8U2BGRAF(unsigned char *Src, float *Dest, int Width, int Height, int Stride)
{
//#pragma omp parallel for
for (int Y = 0; Y < Height; Y++)
{
unsigned char *LinePS = Src + Y * Stride;
float *LinePD = Dest + Y * Width * 3;
for (int X = 0; X < Width; X++, LinePS += 3, LinePD += 3)
{
LinePD[0] = LinePS[0]; LinePD[1] = LinePS[1]; LinePD[2] = LinePS[2];
}
}
}
这个也没有什么技巧可言,就是整数强制转浮点数。这里是普通的C语言实现,所以输出的float数组仍然是3通道的,之后会看到SSE优化后会是4通道的。
GaussBlurFromLeftToRight 水平方向的前向传播
void GaussBlurFromLeftToRight(float *Data, int Width, int Height, float B0, float B1, float B2, float B3)
{
//#pragma omp parallel for
for (int Y = 0; Y < Height; Y++)
{
float *LinePD = Data + Y * Width * 3;
//w[n-1], w[n-2], w[n-3]
float BS1 = LinePD[0], BS2 = LinePD[0], BS3 = LinePD[0]; //边缘处使用重复像素的方案
float GS1 = LinePD[1], GS2 = LinePD[1], GS3 = LinePD[1];
float RS1 = LinePD[2], RS2 = LinePD[2], RS3 = LinePD[2];
for (int X = 0; X < Width; X++, LinePD += 3)
{
LinePD[0] = LinePD[0] * B0 + BS1 * B1 + BS2 * B2 + BS3 * B3;
LinePD[1] = LinePD[1] * B0 + GS1 * B1 + GS2 * B2 + GS3 * B3; // 进行顺向迭代
LinePD[2] = LinePD[2] * B0 + RS1 * B1 + RS2 * B2 + RS3 * B3;
BS3 = BS2, BS2 = BS1, BS1 = LinePD[0];
GS3 = GS2, GS2 = GS1, GS1 = LinePD[1];
RS3 = RS2, RS2 = RS1, RS1 = LinePD[2];
}
}
}
按照前向传播Forward公式来。
GaussBlurFromRightToLeft 水平方向的反向传播
void GaussBlurFromRightToLeft(float *Data, int Width, int Height, float B0, float B1, float B2, float B3) {
for (int Y = 0; Y < Height; Y++) {
//w[n+1], w[n+2], w[n+3]
float *LinePD = Data + Y * Width * 3 + (Width * 3);
float BS1 = LinePD[0], BS2 = LinePD[0], BS3 = LinePD[0]; //边缘处使用重复像素的方案
float GS1 = LinePD[1], GS2 = LinePD[1], GS3 = LinePD[1];
float RS1 = LinePD[2], RS2 = LinePD[2], RS3 = LinePD[2];
for (int X = Width - 1; X >= 0; X--, LinePD -= 3)
{
LinePD[0] = LinePD[0] * B0 + BS3 * B1 + BS2 * B2 + BS1 * B3;
LinePD[1] = LinePD[1] * B0 + GS3 * B1 + GS2 * B2 + GS1 * B3; // 进行反向迭代
LinePD[2] = LinePD[2] * B0 + RS3 * B1 + RS2 * B2 + RS1 * B3;
BS1 = BS2, BS2 = BS3, BS3 = LinePD[0];
GS1 = GS2, GS2 = GS3, GS3 = LinePD[1];
RS1 = RS2, RS2 = RS3, RS3 = LinePD[2];
}
}
}
按照反向传播公式Backward来。
剩下的代码普通的C语言可以在我的github上查看:https://github.com/BBuf/Image-processing-algorithm-Speed/blob/master/speed_gaussian_filter_sse.cpp
SSE优化
这篇文章的重点在于SSE优化,所以接下来会挨个挨个函数分析SSE优化的要点。
对ConvertBGR8U2BGRAF的SSE优化
这里需要对BGR图像新增一个通道,新的通道值这里直接填0。
void ConvertBGR8U2BGRAF_SSE(unsigned char *Src, float *Dest, int Width, int Height, int Stride) {
const int BlockSize = 4;
int Block = (Width - 2) / BlockSize;
__m128i Mask = _mm_setr_epi8(0, 1, 2, -1, 3, 4, 5, -1, 6, 7, 8, -1, 9, 10, 11, -1);
__m128i Zero = _mm_setzero_si128();
for (int Y = 0; Y < Height; Y++) {
unsigned char *LinePS = Src + Y * Stride;
float *LinePD = Dest + Y * Width * 4;
int X = 0;
for (; X < Block * BlockSize; X += BlockSize, LinePS += BlockSize * 3, LinePD += BlockSize * 4) {
__m128i SrcV = _mm_shuffle_epi8(_mm_loadu_si128((const __m128i*)LinePS), Mask);
__m128i Src16L = _mm_unpacklo_epi8(SrcV, Zero);
__m128i Src16H = _mm_unpackhi_epi8(SrcV, Zero);
_mm_store_ps(LinePD + 0, _mm_cvtepi32_ps(_mm_unpacklo_epi16(Src16L, Zero)));
_mm_store_ps(LinePD + 4, _mm_cvtepi32_ps(_mm_unpackhi_epi16(Src16L, Zero)));
_mm_store_ps(LinePD + 8, _mm_cvtepi32_ps(_mm_unpacklo_epi16(Src16H, Zero)));
_mm_store_ps(LinePD + 12, _mm_cvtepi32_ps(_mm_unpackhi_epi16(Src16H, Zero)));
}
for (; X < Width; X++, LinePS += 3, LinePD += 4) {
LinePD[0] = LinePS[0]; LinePD[1] = LinePS[1]; LinePD[2] = LinePS[2]; LinePD[3] = 0;
}
}
}
首先定义了一个BlockSize=4,这是因为SSE是128位,每次可以处理128/8=16个uchar类型的数,其中每一个像素都是4个值,因为这里要新增一个通道。而int Block = (Width - 2) / BlockSize这行代码是因为_mm_loadu_si128一次性加载了5 + 1 / 3个像素值(这里指的是Src),当在处理最后一行像素时,如果Block取Width / BlockSize则有可能会超出像素范围内的内存,而-2则是因为额外的1/3像素起作用。循环挺好理解的,其中_mm_loadu_si128一次性加载16个字节的数据到SSE寄存器中,对于RGB图像 ,16个字节里包含了5+1/3个像素的信息,而我们要做的是把这些数据转换为4个通道的信息,因此,我们只能一次性的提取16/4=4个像素的值,这借助于_mm_shuffle_epi8函数和合适的Mask来实现,_mm_unpacklo_epi8/_mm_unpackhi_epi8分别提取了SrcV的高8位和低8位的8个字节数据并将它们转换为8个16进制数保存到Src16L和Src16H中, 而_mm_unpacklo_epi16/_mm_unpackhi_epi16则进一步把16位数据扩展到32位整形数据,最后通过_mm_cvtepi32_ps函数把整形数据转换为浮点型。
对GaussBlurFromLeftToRight 水平方向的前向传播的SSE优化
void GaussBlurFromLeftToRight_SSE(float *Data, int Width, int Height, float B0, float B1, float B2, float B3) {
const __m128 CofB0 = _mm_set_ps(0, B0, B0, B0);
const __m128 CofB1 = _mm_set_ps(0, B1, B1, B1);
const __m128 CofB2 = _mm_set_ps(0, B2, B2, B2);
const __m128 CofB3 = _mm_set_ps(0, B3, B3, B3);
for (int Y = 0; Y < Height; Y++) {
float *LinePD = Data + Y * Width * 4;
__m128 V1 = _mm_set_ps(LinePD[3], LinePD[2], LinePD[1], LinePD[0]);
__m128 V2 = V1, V3 = V1;
for (int X = 0; X < Width; X++, LinePD += 4) {
__m128 V0 = _mm_load_ps(LinePD);
__m128 V01 = _mm_add_ps(_mm_mul_ps(CofB0, V0), _mm_mul_ps(CofB1, V1));
__m128 V23 = _mm_add_ps(_mm_mul_ps(CofB2, V2), _mm_mul_ps(CofB3, V3));
__m128 V = _mm_add_ps(V01, V23);
V3 = V2; V2 = V1; V1 = V;
_mm_store_ps(LinePD, V);
}
}
}
这里ImageShop提到了之所以没有使用_mm_storeu_ps而是直接使用_mm_store_ps是因为分配Data内存时,采用了_mm_malloc分配了16字节对齐的内存,而Data每行元素的个数又是4的倍数,因此每行起始位置处的内存也是16字节对齐的,所以字节_mm_store_ps是可行的。
之后的水平方向的反向传播,垂直方向的传播代码均可以在我的github找到:https://github.com/BBuf/Image-processing-algorithm-Speed/blob/master/speed_gaussian_filter_sse.cpp
还有作者没有提供ConvertBGRAF2BGR8U的SSE的代码,这一段要进行SSE优化的难度确实是蛮大的,我实现的瓶颈在于我不知道如何将SSE向量映射为只保存3个值的一个像素,这里我还需要再继续探索下去,我先给一份我的普通实现(没有SSE优化):
void ConvertBGRAF2BGR8U_SSE(float *Src, unsigned char *Dest, int Width, int Height, int Stride) {
for (int Y = 0; Y < Height; Y++) {
float *LinePS = Src + Y * Width * 4;
unsigned char *LinePD = Dest + Y * Stride;
for (int X = 0; X < Width; X++, LinePS += 4, LinePD += 3) {
LinePD[0] = LinePS[0]; LinePD[1] = LinePS[1]; LinePD[2] = LinePS[2];
}
}
}
时间测试
普通版和SSE优化版(没有最后一个颜色通道转换的优化)完整的代码可以在我的github找到,现在我给出我的时间测试表,Corei7 8770单核,图片分辨率为4032*3024:
| 优化技巧编号 | 优化技巧名称 | 时间 | 半径 |
|---|---|---|---|
| 1 | 无优化 | 290.43ms | 11 |
| 2 | SSE优化 | 265.96ms | 11 |




 京公网安备 11010502036488号
京公网安备 11010502036488号