对于正整数

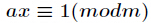
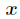


逆元一般用扩展欧几里得算法来求得,如果
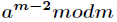
推导过程如下
求现在来看一个逆元最常见问题,求如下表达式的值(已知
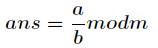
当然这个经典的问题有很多方法,最常见的就是扩展欧几里得,如果
但是你会发现费马小定理和扩展欧几里得算法求逆元是有局限性的,它们都会要求

种通用的求逆元方法,适合所有情况。公式如下
现在我们来证明它,已知
逆元公式:
因为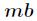
其实有些题需要用到


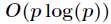
如果对于一个1000000级别的素数
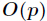
它的推导过程如下,设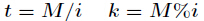
对上式两边同时除
再把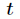
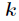
初始化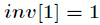


另外


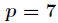
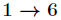
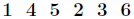
逆元:
然而乘法逆元的应用也需要条件:
对于乘法逆元:在mod m的操作下(即Zm中),a存在乘法逆元当且仅当a与m互质。不定方程ab+mx=1的任意一组整数解(b,x),b就是a的乘法逆元。具体计算可以使用扩展欧几里德算法(Extended-GCD)。
kuangbin神给的模板
- //返回d=gcd(a,b);和对应于等式ax+by=d中的x,y
- long long extend_gcd(long long a,long long b,long long &x,long long &y)
- {
- if(a==0&&b==0) return -1;//无最大公约数
- if(b==0){x=1;y=0;return a;}
- long long d=extend_gcd(b,a%b,y,x);
- y-=a/b*x;
- return d;
- }
- //*********求逆元素*******************
- //ax = 1(mod n)
- long long mod_reverse(long long a,long long n)
- {
- long long x,y;
- long long d=extend_gcd(a,n,x,y);
- if(d==1) return (x%n+n)%n;
- else return -1;
- }
以下两种写法都必须要求MOD为素数
1.#define Inv(x) (Pow(x,MOD-2))
由x^(m-1) ≡ 1 (mod m)(费马小定理)
故 x* x^(m-2)≡ 1 (mod m),显然x对模m的逆元是x^(m-2)
2.还有一种写法(来源)
可以O(n)时间求逆
- int[] inv = new int[MAXN];
- inv[1] = 1;
- for (int i = 2; i<MAXN; i++)
- inv[i] = inv[MOD%i]*(MOD-MOD/i)%MOD;
- // m^n % k
- long long quickpow(long long m,long long n,long long k)
- {
- long long b = 1;
- while (n > 0)
- {
- if (n & 1)
- b = (b*m)%k;
- n = n >> 1 ;
- m = (m*m)%k;
- }
- return b;
- }
贴一个关于逆元的链接:http://blog.csdn.net/cqlf__/article/details/7953039



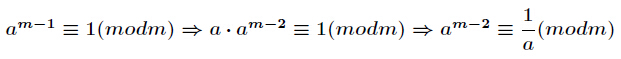
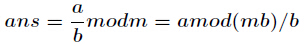
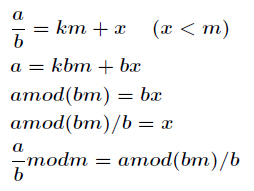
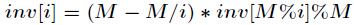
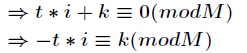
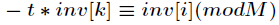

 京公网安备 11010502036488号
京公网安备 11010502036488号