描述
题目描述
给定了我们一个二叉树,然后让我们进行这样的一个操作,按照奇数层从左到右,偶数层从右向左,存入我们的数组,然后输出
样例解释
样例输入:
{1,2,3,#,#,4,5}
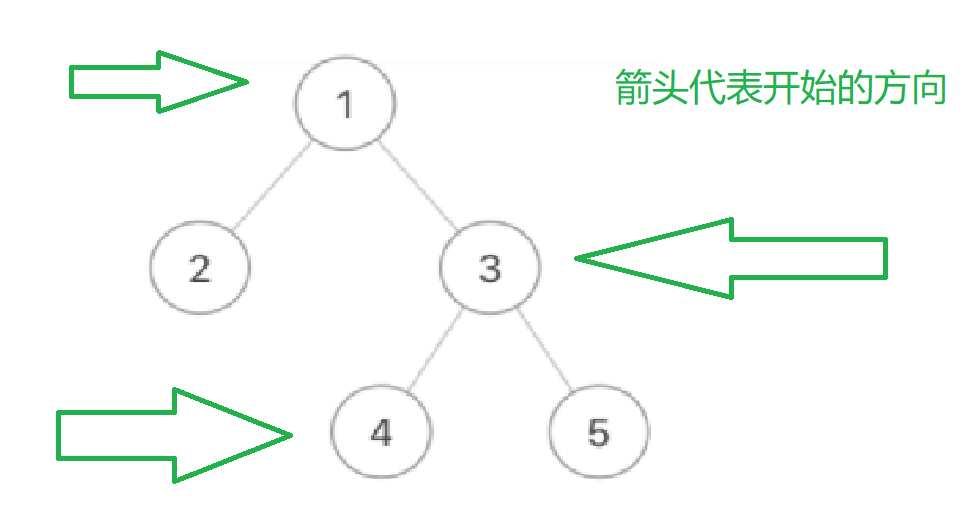
所以我们的样例输出是
[[1],[3,2],[4,5]]
解法
解法一:
实现思路
其实这个我们很容易可以想到,我们按照根节点->左子树->右子树的这个顺序遍历的话,我们可以保证我们的每一层里面的所有节点以从左到右的顺序排列出来,然后我们直接遍历一次就可以了, 然后我们如果从认为根节点那层是的话, 那么我们就是最后奇数层反转
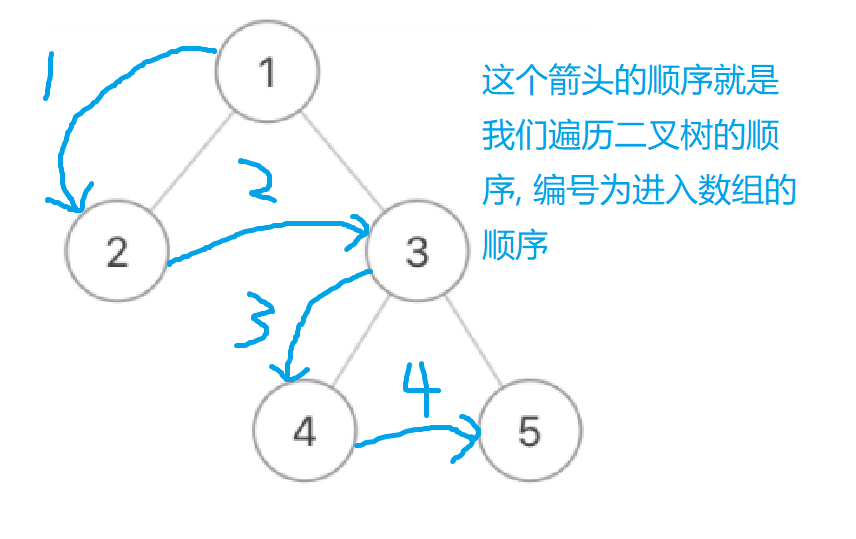
代码实现
class Solution {
int maxx = 0;
// 获取我们的二叉树的最大的深度
public:
void getLength(TreeNode *root, int cnt) {
if (root == nullptr) return;
maxx = max(maxx, cnt);
if (root->left != nullptr) getLength(root->left, cnt + 1);
if (root->right != nullptr) getLength(root->right, cnt + 1);
}
// 我们递归遍历一次我们的整个的二叉树, 然后我们获取到我们的最大的深度
void dfs(TreeNode *root, int cnt, vector<vector<int>> &res) {
if (root == nullptr) return;
res[cnt].push_back(root->val);
// 我们每次把我们的答案放入我们的二维数组中
if (root->left != nullptr) dfs(root->left, cnt + 1, res);
if (root->right != nullptr) dfs(root->right, cnt + 1, res);
}
// 因为我们是按照根节点左子树,右子树的方式遍历,所以我们可以保证每一层都是按顺序的
vector<vector<int>> Print(TreeNode *pRoot) {
if (pRoot == nullptr) return {};
// 这里第19组数据会有问题,如果不加这个的话,虽然我们返回的也是空,但是还是申请了一个空间
getLength(pRoot, 0);
vector<vector<int>> res(maxx + 1);
dfs(pRoot, 0, res);
for (int i = 0; i < res.size(); i++) {
if (i & 1) reverse(res[i].begin(), res[i].end());
}
// 反转我们的奇数层
return res;
}
};
时空复杂度分析
时间复杂度:
理由如下: 递归遍历我们二叉树的复杂度
空间复杂度:
理由如下: 极限情况下退化成为链, 递归栈的空间为
解法二
实现思路
我们除了可以使用递归的方法遍历我们的这个二叉树之外, 我们还可以考虑使用迭代的方式也是我们的来遍历我们的这颗二叉树, 思路与上面类似
代码实现
class Solution {
vector<vector<int>> res;
public:
vector<vector<int>> Print(TreeNode *pRoot) {
if (pRoot == nullptr) return {};
// 空指针直接返回
queue<TreeNode *> q;
// 作为我们的这个bfs的队列
q.push(pRoot);
// 先放入我们的根节点
while (q.size()) {
int len = q.size();
vector<int> tmp;
// 获取当前的长度
for (; len; len--) {
auto t = q.front();
q.pop();
// 每次导入
tmp.push_back(t->val);
if (t->left != nullptr) q.push(t->left);
if (t->right != nullptr) q.push(t->right);
// 放入他的叶子节点, 然后把当前节点放入我们数组
}
res.push_back(tmp);
}
for (int i = 0; i < res.size(); i++) {
if (i & 1) reverse(res[i].begin(), res[i].end());
}
// 反转
return res;
}
};
时空复杂度分析
时间复杂度:
理由如下: 递归遍历我们二叉树的复杂度
空间复杂度:
理由如下: 极限情况我们会存储一半的节点在我们的对列中, 所以我们的空间复杂度实际上还是






 京公网安备 11010502036488号
京公网安备 11010502036488号