描述

题目描述

首先给我们一个字符串，这个字符串里面含有$+,-,(,)+,\; -,\; (,\; )$，然后运算的优先级跟我们正常算数的运算优先级一样，让我们求出最后的值

样例解释

"1+2"

这个我们直接计算就可以，得到$33$

所以最后的输出是

3

需要注意

这里我们会有括号嵌套的情况，这里我们需要特殊注意一下顺序

题解

解法一：栈

解题思路

其实我们的这个整个操作都是可以分成三部分

$\mathrm{左}\mathrm{边}\mathrm{表}\mathrm{达}\mathrm{式}-\mathrm{运}\mathrm{算}\mathrm{符}-\mathrm{右}\mathrm{边}\mathrm{表}\mathrm{达}\mathrm{式}左边表达式-运算符-右边表达式$

然后这里我们可以使用栈来保存我们的左边表达式和符号位，我们每次计算完之后都更新一下，然后在于右边表达式进行操作，然后如果遇到了括号的嵌套，我们可以一直进栈，直到遇到右括号，这样我们可以保证我们的栈顶的元素就是我们的括号里面的运算结果

也就式我们要维护这么几个变量

1. 左边表达式的值
2. 当前运算符
3. 当前遇到的数字
4. 栈

总体过程可以如下图所示

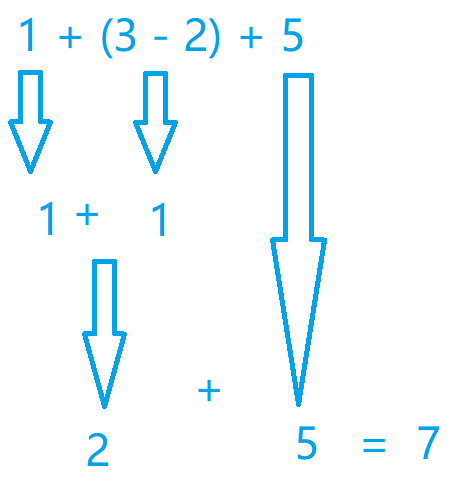
代码实现

class Solution {
public:
    int calculate(string s) {
        stack<int> num;
        stack<char> sign;
//         分别用于存储符号位和数值位
        int tmp = 0, sig = 1, res = 0;
//         这个分别式我们上一个的值，每一次的符号，和我们最后的答案
        for (auto &it : s) {
//             遍历我们的字符串
            if (it >= '0' and it <= '9') tmp = tmp * 10 + (it - '0');
//             这个是为了避免我们有多位，我们的数字不只一位
            else if (it == '+' or it == '-') {
//                 如果是加减法，我们进行一个运算
                res += sig * tmp;
                tmp = 0;
                it == '+' ? sig = 1 : sig = -1;
//                 更改我们的临时元素
            } else if (it == '(') {
//                 如果是括号的话，一直入栈
                num.push(res);
                sign.push(sig);
                res = 0, sig = 1;
            } else if (it == ')') {
//                 不断计算我们的值，然后出栈
                res += sig * tmp;
                tmp = 0;
                res *= sign.top();
                sign.pop();
                res += num.top();
                num.pop();
            }
        }
        res += sig * tmp;
//         把最后一位也给算上
        return res;
    }
};

时空复杂度分析

时间复杂度： $O(n)O(n)$

理由如下：主要的时间就是遍历了我们这个字符串的长度

空间复杂度： $O(n)O(n)$

理由如下：我们开辟了一个栈用于存储我们的数据和符号

解法二：模拟

解题思路

我们上面的方法还是考虑了括号，这里我们可以想一种更为暴力的做法，直接用我们的正负号把我们的括号完全拆开，只要考虑每次的符号即可和变号即可

代码实现

class Solution {
public:
    int calculate(string s) {
        stack<int> sign;
        int res = 0, tmp = 0, sig = 1;
//         分别位最后的答案，临时数，符号
        sign.push(sig);
//         我们开辟的栈用于存储符号
        for (auto &it : s) {
            if (it >= '0' and it <= '9') tmp = tmp * 10 + (it - '0');
//             避免这个数是多位数
            else {
                res += tmp * sig, tmp = 0;
//                 计算结果
                switch (it) {
                    case '+':
                        sig = sign.top();
                        break;
                    case '-':
                        sig = -sign.top();
                        break;
                    case '(':
                        sign.push(sig);
                        break;
                    default:
                        sign.pop();
                        break;
                }
//                 让我们从这里开始的符号位进行改变
            }
        }
        res += sig * tmp;
//         把最后一个也算进去
        return res;
    }
};

时空复杂度分析

时间复杂度： $O(n)O(n)$

理由如下：主要的时间就是遍历了我们这个字符串的长度

空间复杂度： $O(n)O(n)$

理由如下：我们开辟了一个栈用于存储我们的符号