今天主要讲的是递归和DFS,因为涉及到递归,很抽象,所以比较难理解。题也很难做。
Oil Deposits
Description:
The GeoSurvComp geologic survey company is responsible for detecting underground oil deposits. GeoSurvComp works with one large rectangular region of land at a time, and creates a grid that divides the land into numerous square plots. It then analyzes each plot separately, using sensing equipment to determine whether or not the plot contains oil. A plot containing oil is called a pocket. If two pockets are adjacent, then they are part of the same oil deposit. Oil deposits can be quite large and may contain numerous pockets. Your job is to determine how many different oil deposits are contained in a grid.
Input
The input file contains one or more grids. Each grid begins with a line containing m and n, the number of rows and columns in the grid, separated by a single space. If m = 0 it signals the end of the input; otherwise 1 <= m <= 100 and 1 <= n <= 100. Following this are m lines of n characters each (not counting the end-of-line characters). Each character corresponds to one plot, and is either `*', representing the absence of oil, or `@', representing an oil pocket.
Output
For each grid, output the number of distinct oil deposits. Two different pockets are part of the same oil deposit if they are adjacent horizontally, vertically, or diagonally. An oil deposit will not contain more than 100 pockets.
Sample Input
1 1 * 3 5 *@*@* **@** *@*@* 1 8 @@****@* 5 5 ****@ *@@*@ *@**@ @@@*@ @@**@ 0 0
Sample Output
0
1
2
2
Problem solving:
简单题,输入一个图,@表示油田,*表示没有油田,@只要是相邻的都可以算成是一个,所以就是八个方向上dfs就行,访问过的@就换成*或者其他的字符就行只要不是@.(如果这样写的话其实就不需要标记数组了)
Code:
#include<bits/stdc++.h>
using namespace std;
char s[105][105];
int vis[105][105];
int m,n,ans;
int d[8][2]={1,0,0,1,0,-1,-1,0,1,1,1,-1,-1,-1,-1,1};
void dfs(int x,int y)
{
vis[x][y]=1;
if(x<0||x>=m||y<0||y>=n) return ;
for(int i=0;i<8;i++)
{
int dx=x+d[i][0];
int dy=y+d[i][1];
if(dx>=0&&dx<m&&dy>=0&&dy<n&&!vis[dx][dy]&&s[dx][dy]=='@')
{
s[dx][dy]='*';
dfs(dx,dy);
}
}
}
int main()
{
while(cin>>m>>n&&m)
{
memset(vis,0,sizeof(vis));
ans=0;
for(int i=0;i<m;i++) cin>>s[i];
for(int i=0;i<m;i++)
{
for(int j=0;j<n;j++)
{
if(s[i][j]=='@')
{
dfs(i,j);
ans++;
}
}
}
cout<<ans<<endl;
}
}How Many Equations Can You Find
Description:
Now give you an string which only contains 0, 1 ,2 ,3 ,4 ,5 ,6 ,7 ,8 ,9.You are asked to add the sign ‘+’ or ’-’ between the characters. Just like give you a string “12345”, you can work out a string “123+4-5”. Now give you an integer N, please tell me how many ways can you find to make the result of the string equal to N .You can only choose at most one sign between two adjacent characters.
Input
Each case contains a string s and a number N . You may be sure the length of the string will not exceed 12 and the absolute value of N will not exceed 999999999999.
Output
The output contains one line for each data set : the number of ways you can find to make the equation.
Sample Input
123456789 3
21 1
Sample Output
18
1
Problem solving:
暂无(毫无思路题)
Code:
/** * ┏┓ ┏┓ * ┏┛┗━━━━━━━┛┗━━━┓ * ┃ ┃ * ┃ ━ ┃ * ┃ > < ┃ * ┃ ┃ * ┃... ⌒ ... ┃ * ┃ ┃ * ┗━┓ ┏━┛ * ┃ ┃ Code is far away from bug with the animal protecting * ┃ ┃ 神兽保佑,代码无bug * ┃ ┃ * ┃ ┃ * ┃ ┃ * ┃ ┃ * ┃ ┗━━━┓ * ┃ ┣┓ * ┃ ┏┛ * ┗┓┓┏━┳┓┏┛ * ┃┫┫ ┃┫┫ * ┗┻┛ ┗┻┛ */ // warm heart, wagging tail,and a smile just for you! // // _ooOoo_ // o8888888o // 88" . "88 // (| -_- |) // O\ = /O // ____/`---'\____ // .' \| |// `. // / \||| : |||// \ // / _||||| -:- |||||- \ // | | \\ - /// | | // | \_| ''\---/'' | | // \ .-\__ `-` ___/-. / // ___`. .' /--.--\ `. . __ // ."" '< `.___\_<|>_/___.' >'"". // | | : `- \`.;`\ _ /`;.`/ - ` : | | // \ \ `-. \_ __\ /__ _/ .-` / / // ======`-.____`-.___\_____/___.-`____.-'====== // `=---=' // ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ //
N皇后问题
Description:
在N*N的方格棋盘放置了N个皇后,使得它们不相互攻击(即任意2个皇后不允许处在同一排,同一列,也不允许处在与棋盘边框成45角的斜线上。
你的任务是,对于给定的N,求出有多少种合法的放置方法。
Input
共有若干行,每行一个正整数N≤10,表示棋盘和皇后的数量;如果N=0,表示结束。
Output
共有若干行,每行一个正整数,表示对应输入行的皇后的不同放置数量。
Sample Input
1
8
5
0
Sample Output
1
92
10
Problem solving:
从第一行开始放,然后放下一行,如果出现了在同一行的或者同一列的或者同一条斜线上的就return,如果放进去的个数等于n,答案就加一。这道题N虽然小于等于10,但是是多组输入,如果每次输入都计算一次并且输入数据很多的话,肯定会TLE。所以需要打表,就是如果这个计算过了就把它的结果记录下来,如果下次又要求这个的结果直接调用就行。也可以直接从输入前就先计算好存进数组。
Code:
#include<bits/stdc++.h>
using namespace std;
int n,mid;
int ans[12],mmp[12];
void dfs(int x)
{
if(x==n+1)
{
mid++;
return ;
}
for(int i=1;i<=n;i++)
{
int flag=1;
mmp[x]=i;
for(int j=1;j<x;j++)
{
if(mmp[j]==i||(abs(j-x)==abs(mmp[j]-mmp[x])))
{
flag=0;
break;
}
}
if(flag) dfs(x+1);
}
}
int main()
{
for(n=1;n<=10;n++)
{
mid=0;
dfs(1);
ans[n]=mid;
}
int t;
while(cin>>t&&t)
{
cout<<ans[t]<<endl;
}
}Fox And Two Dots
Description:
Fox Ciel is playing a mobile puzzle game called "Two Dots". The basic levels are played on a board of size n × m cells, like this:
Each cell contains a dot that has some color. We will use different uppercase Latin characters to express different colors.
The key of this game is to find a cycle that contain dots of same color. Consider 4 blue dots on the picture forming a circle as an example. Formally, we call a sequence of dots d1, d2, ..., dk a cycle if and only if it meets the following condition:
- These k dots are different: if i ≠ j then di is different from dj.
- k is at least 4.
- All dots belong to the same color.
- For all 1 ≤ i ≤ k - 1: di and di + 1 are adjacent. Also, dk and d1 should also be adjacent. Cells x and y are called adjacent if they share an edge.
Determine if there exists a cycle on the field.
Input
The first line contains two integers n and m (2 ≤ n, m ≤ 50): the number of rows and columns of the board.
Then n lines follow, each line contains a string consisting of m characters, expressing colors of dots in each line. Each character is an uppercase Latin letter.
Output
Output "Yes" if there exists a cycle, and "No" otherwise.
Examples
Input
3 4
AAAA
ABCA
AAAA
Output
Yes
Input
3 4
AAAA
ABCA
AADA
Output
No
Input
4 4
YYYR
BYBY
BBBY
BBBY
Output
Yes
Input
7 6
AAAAAB
ABBBAB
ABAAAB
ABABBB
ABAAAB
ABBBAB
AAAAAB
Output
Yes
Input
2 13
ABCDEFGHIJKLM
NOPQRSTUVWXYZ
Output
No
Note
In first sample test all 'A' form a cycle.
In second sample there is no such cycle.
The third sample is displayed on the picture above ('Y' = Yellow, 'B' = Blue, 'R' = Red).
Problem solving:
这道题的意思就是输入一个由大写字母组成的图,如果相同的字母可以组成一个环,就输出Yes,否则输出No。
这道题跟昨天的那个机器人有点类似,不过那个机器人每次走的方向是定的,而这个是可以随意走的。
所以如何进行判断会不会有环的存在呢?
我们只需要在每次进行dfs的查找之前把最初的初始位置记录一下,然后开始dfs查找,上下左右四个方向,遇到与当前字母一样的字母就以这个为初始位置继续dfs,并且记录下来当前走的步数。如果在dfs结束之前遇到了一个(dx,dy)与我们记录的最初始的初始位置相等并且步数大于等于4的情况,就说明存在环,输出'Yes'即可,反之输出'No'。
Code:
#include<bits/stdc++.h>
using namespace std;
char s[60][60];
int vis[60][60],flag,n,m,sx,sy;
int d[4][2]={1,0,0,1,-1,0,0,-1};
void dfs(int x,int y,int step)
{
if(flag) return ;
vis[x][y]=1;
for(int i=0;i<4;i++)
{
int dx=x+d[i][0];
int dy=y+d[i][1];
if(dx==sx&&dy==sy&&step>=4)
{
flag=1;
return ;
}
if(dx>=0&&dx<n&&dy>=0&&dy<m&&!vis[dx][dy]&&s[dx][dy]==s[x][y])
{
dfs(dx,dy,step+1);
}
}
}
int main()
{
cin>>n>>m;
for(int i=0;i<n;i++) cin>>s[i];
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++)
{
memset(vis,0,sizeof(vis));
sx=i,sy=j;
dfs(sx,sy,1);
}
}
if(flag) puts("Yes");
else puts("No");
}棋盘问题
Description:
在一个给定形状的棋盘(形状可能是不规则的)上面摆放棋子,棋子没有区别。要求摆放时任意的两个棋子不能放在棋盘中的同一行或者同一列,请编程求解对于给定形状和大小的棋盘,摆放k个棋子的所有可行的摆放方案C。
Input
输入含有多组测试数据。
每组数据的第一行是两个正整数,n k,用一个空格隔开,表示了将在一个n*n的矩阵内描述棋盘,以及摆放棋子的数目。 n <= 8 , k <= n
当为-1 -1时表示输入结束。
随后的n行描述了棋盘的形状:每行有n个字符,其中 # 表示棋盘区域, . 表示空白区域(数据保证不出现多余的空白行或者空白列)。
Output
对于每一组数据,给出一行输出,输出摆放的方案数目C (数据保证C<2^31)。
Sample Input
2 1 #. .# 4 4 ...# ..#. .#.. #... -1 -1
Sample Output
2
1
Problem solving:
跟n皇后很像的一个问题。判断条件还少了一个。注意回溯就行。
Code:
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
int n,k,vis[10],ans,now;
char s[10][10];
void dfs(int x)
{
if(now==k)
{
ans++;
return ;
}
if(x>=n) return ;
for(int j=0;j<n;j++)
{
if(!vis[j]&&s[x][j]=='#')
{
vis[j]=1;
now++;
dfs(x+1);
now--;
vis[j]=0;
}
}
dfs(x+1);
}
int main()
{
while(scanf("%d %d",&n,&k)&&n!=-1&&k!=-1)
{
memset(vis,0,sizeof(vis));
for(int i=0;i<n;i++) cin>>s[i];
ans=0,now=0;
dfs(0);
cout<<ans<<endl;
}
}Sudoku
Description:
Sudoku is a very simple task. A square table with 9 rows and 9 columns is divided to 9 smaller squares 3x3 as shown on the Figure. In some of the cells are written decimal digits from 1 to 9. The other cells are empty. The goal is to fill the empty cells with decimal digits from 1 to 9, one digit per cell, in such way that in each row, in each column and in each marked 3x3 subsquare, all the digits from 1 to 9 to appear. Write a program to solve a given Sudoku-task.
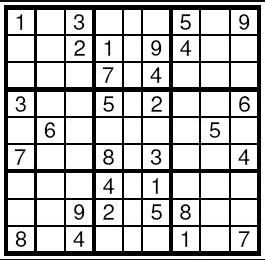
Input
The input data will start with the number of the test cases. For each test case, 9 lines follow, corresponding to the rows of the table. On each line a string of exactly 9 decimal digits is given, corresponding to the cells in this line. If a cell is empty it is represented by 0.
Output
For each test case your program should print the solution in the same format as the input data. The empty cells have to be filled according to the rules. If solutions is not unique, then the program may print any one of them.
Sample Input
1
103000509
002109400
000704000
300502006
060000050
700803004
000401000
009205800
804000107
Sample Output
143628579
572139468
986754231
391542786
468917352
725863914
237481695
619275843
854396127
Problem solving:
这道题的处理方式很巧妙。dfs中的参数只设置一个n(n就是代表着这是第几个数)就够了,就是当前的位置,在dfs中每次加一,如果当前位置不为0,就直接查找下一个位置。否则就从1~9中选一个数放进去,看同一行同一列以及同一小方格的同一行同一列有没有与之相同的,如果没有,就将当前位置的数更新成这个没有重复出现过的数。知道查找到n>=81的时候,即每个位置都查找完了,结束查找输出即可。注意在查找的过程中需要用到回溯,因为如果这一条路行不通而返回上一条路的时候,此时当前位置还应该是0.
思路还是很清晰的,难点主要有两个
- 如何用n来表示当前的位置
- 如何判断同一行同一列以及同一小方格的同一行同一列有没有与之相同的数
n/9代表的就是当前位置的行,n%9代表的就是当前位置的列。
n/9/3*3表示的就是当前位置在小方格里的行,n%9/3*3代表的就是当前位置在小方格里的列。
位置都能表示出来了,那么判断也就简单了。
分别确定二维数组的第一个和第二个坐标进行判断就行了。这一点可能说的不是很好理解,可以看看代码,还是很好理解的。
Code:
#include<iostream>
#include<cstdio>
using namespace std;
int a[10][10],flag;
bool check(int n,int now)
{
for(int i=0;i<9;i++)
{
int j=n%9;
if(a[i][j]==now)
return 0;
}
for(int j=0;j<9;j++)
{
int i=n/9;
if(a[i][j]==now)
return 0;
}
int di=n/9/3*3;
int dj=n%9/3*3;
for(int i =di;i<di+3;i++)
{
for(int j=dj;j<dj+3;j++)
{
if(a[i][j]==now) return 0;
}
}
return 1;
}
int dfs(int n)
{
if(n>=81)
{
flag=1;
return 0;
}
if(a[n/9][n%9]!=0) dfs(n+1);
else
{
for(int i=1;i<=9;i++)
{
if(check(n,i)==1)
{
a[n/9][n%9]=i;
dfs(n+1);
if(flag==1)
return 0;
a[n/9][n%9]=0;//回溯
}
}
}
// cout<<"?"<<endl;
}
int main()
{
int t;
cin>>t;
while(t--)
{
flag=0;
for(int i=0;i<9;i++)
for(int j=0;j<9;j++)
scanf("%1d",&a[i][j]);
dfs(0);
for(int i=0;i<9;i++)
{
for(int j=0;j<9;j++)
printf("%d",a[i][j]);
puts("");
}
}
return 0;
}放苹果
Description:
把M个同样的苹果放在N个同样的盘子里,允许有的盘子空着不放,问共有多少种不同的分法?(用K表示)5,1,1和1,5,1 是同一种分法。
Input
第一行是测试数据的数目t(0 <= t <= 20)。以下每行均包含二个整数M和N,以空格分开。1<=M,N<=10。
Output
对输入的每组数据M和N,用一行输出相应的K。
Sample Input
1
7 3
Sample Output
8
Problem solving:
思维题。(让我说也说不清,还是借用一下大佬的解释吧)
设f(m,n) 为m个苹果,n个盘子的放法数目,则先对n作讨论,
当n>m:必定有n-m个盘子永远空着,去掉它们对摆放苹果方法数目不产生影响。即if(n>m) f(m,n) = f(m,m)
当n<=m:不同的放法可以分成两类:
1、有至少一个盘子空着,即相当于f(m,n) = f(m,n-1);
2、所有盘子都有苹果,相当于可以从每个盘子中拿掉一个苹果,不影响不同放法的数目,即f(m,n) = f(m-n,n).
而总的放苹果的放法数目等于两者的和,即 f(m,n) =f(m,n-1)+f(m-n,n)
递归出口条件说明:
当n=1时,所有苹果都必须放在一个盘子里,所以返回1;
当没有苹果可放时,定义为1种放法;
递归的两条路,第一条n会逐渐减少,终会到达出口n==1;
第二条m会逐渐减少,因为n>m时,我们会return f(m,m) 所以终会到达出口m==0.
此解释源于:https://blog.csdn.net/jason0539/article/details/12183817
Code:
#include<iostream>
using namespace std;
int t,n,m,ans;
int dfs(int x,int y)
{
if(x==0||y==1){
return 1;
}
else if(x<y) return dfs(x,x);
return dfs(x,y-1)+dfs(x-y,y);
}
int main()
{
cin>>t;
while(t--)
{
cin>>m>>n;
cout<<dfs(m,n)<<endl;
}
}Tempter of the Bone
Description:
小明做了一个很久很久的梦,醒来后他竟发现自己和朋友在一个摇摇欲坠的大棋盘上,他们必须得想尽一切办法逃离这里。
经过长时间的打探,小明发现,自己所在的棋盘格子上有个机关,上面写着“你只有一次机会,出发后t秒大门会为你敞开”,而他自己所在的棋盘是大小为 N*M 的长方形,他可以向上下左右四个方向移动(不可走有障碍点)。棋盘中有一扇门。根据机关的提示,小明顿时明白了,他和朋友必须在第 t 秒到门口。而这一切,没有回头路!因为一旦他移动了,他刚才所在的点就会消失,并且他不能在一个点上停留超过一秒,不然格子会爆炸。大逃亡开始了,请问小明和朋友能安全的逃出这奇怪的棋盘吗?
Input
输入多组测试数据。每个测试用例的第一行包含三个整数 N、M 和 T ( 1 < N , M < 7 ; 0 < T < 50 ),分别表示棋盘的大小和门打开的时间。接下来的N行给出棋盘布局,每一行包含M个字符。其中
".": 无障碍点
"X": 障碍点
"S": 起点
"D": 门
输入以 3 个 0 结束。这个测试用例不需要处理。
输入数据中的空格有些问题,请不要使用getchar(),如果一定要用可以选择scanf("%s",) 自动忽略空格
Output
对于每组样例输出一行。
如果小明能够安全逃出,输出 "YES" ,否则输出 "NO"。
Sample Input
4 4 5 S.X. ..X. ..XD .... 3 4 5 S.X. ..X. ...D 0 0 0
Sample Output
NO
YES
Problem solving:
注意题目中要求的是当你走到D的时候你走的步数与它开门的时间即T相等,所以需要用DFS查找每一条到达D的路,看与T相等的值是否存在。
因为要查询到每一条路,这道题可能会超时。所以会用到一种很神奇的剪枝——奇偶剪枝
现在hdu在打多校交不了代码,一会如果过了我就贴上来。
Code:
#include<bits/stdc++.h>
using namespace std;
int n,m,t,sx,sy,ex,ey,ti,flag;
char s[10][10];
int vis[10][10];
int d[4][2]={0,1,0,-1,1,0,-1,0};
void dfs(int x,int y)
{
if(x<0||x>=n||y<0||y>=m||ti>t) return ;
if(flag) return ;
if(s[x][y]=='D'&&ti==t)
{
// cout<<ti<<endl;
flag=1;
return ;
}
int temp1 = abs(ex-x) + abs(ey-y);
int temp2 = abs(t-ti);
int temp = abs(temp1-temp2);
if(temp%2!=0) return ;
vis[x][y]=1;
for(int i=0;i<4;i++)
{
int dx=x+d[i][0];
int dy=y+d[i][1];
if(dx>=0&&dx<n&&dy>=0&&dy<m&&!vis[dx][dy]&&s[dx][dy]!='X')
{
// cout<<ti<<"-->"<<dx<<" -->"<<dy<<"\n";
ti++;
dfs(dx,dy);
vis[dx][dy]=0;
ti--;
}
}
}
int main()
{
ios::sync_with_stdio(0);
while(cin>>n>>m>>t)
{
if(n==0&&m==0&&t==0) break;
flag=0,ti=0;
memset(vis,0,sizeof(vis));
for(int i=0;i<n;i++) cin>>s[i];
for(int i=0;i<n;i++)
for(int j=0;j<m;j++)
if(s[i][j]=='S')
{
sx=i,sy=j;
}
else if(s[i][j]=='D')
{
ex=i,ey=j;
}
dfs(sx,sy);
if(flag) puts("YES");
else puts("NO");
}
}Red and Black
Description:
There is a rectangular room, covered with square tiles. Each tile is colored either red or black. A man is standing on a black tile. From a tile, he can move to one of four adjacent tiles. But he can't move on red tiles, he can move only on black tiles.
Write a program to count the number of black tiles which he can reach by repeating the moves described above.
Input
The input consists of multiple data sets. A data set starts with a line containing two positive integers W and H; W and H are the numbers of tiles in the x- and y- directions, respectively. W and H are not more than 20.
There are H more lines in the data set, each of which includes W characters. Each character represents the color of a tile as follows.
'.' - a black tile
'#' - a red tile
'@' - a man on a black tile(appears exactly once in a data set)
Output
For each data set, your program should output a line which contains the number of tiles he can reach from the initial tile (including itself).
Sample Input
6 9 ....#. .....# ...... ...... ...... ...... ...... #@...# .#..#. 11 9 .#......... .#.#######. .#.#.....#. .#.#.###.#. .#.#..@#.#. .#.#####.#. .#.......#. .#########. ........... 11 6 ..#..#..#.. ..#..#..#.. ..#..#..### ..#..#..#@. ..#..#..#.. ..#..#..#.. 7 7 ..#.#.. ..#.#.. ###.### ...@... ###.### ..#.#.. ..#.#.. 0 0
Sample Output
45
59
6
13
Problem solving:
对没错就是昨天那道题,用bfs可以写,用dfs也可以写。太强了。只要下一个还是可以走得就一直dfs查找下去就行。
Code:
#include<bits/stdc++.h>
using namespace std;
char s[25][25];
int vis[25][25];
int a,b,ans;
int d[4][2]={1,0,0,1,0,-1,-1,0};
void dfs(int x,int y)
{
vis[x][y]=1;
if(x<0||x>=b||y<0||y>=a) return ;
for(int i=0;i<4;i++)
{
int dx=x+d[i][0];
int dy=y+d[i][1];
if(dx>=0&&dx<b&&dy>=0&&dy<a&&!vis[dx][dy]&&s[dx][dy]!='#')
{
ans++;
dfs(dx,dy);
}
}
}
int main()
{
while(cin>>a>>b)
{
if(a==0&&b==0) break;
ans=1;
memset(vis,0,sizeof(vis));
for(int i=0;i<b;i++)
{
for(int j=0;j<a;j++)
{
cin>>s[i][j];
}
}
for(int i=0;i<b;i++)
for(int j=0;j<a;j++)
{
if(s[i][j]=='@') dfs(i,j);
}
cout<<ans<<endl;
}
}



 京公网安备 11010502036488号
京公网安备 11010502036488号