数据结构错题

易错题

1. _______是数据结构的基本单位，______是数据不可分割的最小单位。

   数据元素; 数据项

2. 常用的建堆算法是_______。

   筛选法

3. 数据结构从逻辑上可以分为________结构和______结构。

   线性; 非线性

4. 连通图的极小连通子图称为该图的_________。

   最小生成树

5. 压缩矩阵一般的压缩方法有两种分别为：________ 和________。

   三元组；十字链表

6. n个记录进行简单插入排序，最少需要比较多少次？最多需要比较多少次？

   最少：n-1， 最多：n(n-1)/2

7. 判断：在链队列中，除了队头指针外，还必须设队尾指针，否则无法进行队列的插入操作。

   错误，可以不设立队尾指针，只是效率会下降。

8. 对长度为$2^{k}2^k$的有序表进行折半查找，最多比较多少次？查找失败的平均次数是多少？

   最多比较: $\lceil lo{g}_2(2^k+1)\rceil \backslash lceil\; log\_2\; (2^k+1)\backslash rceil$, 平均比较次数: $((2^k-1)k+(k+1)2)\mathrm{/}(2^k+1)((2^k-1)k\; +\; (k+1)2)/(2^k+1)$

9. 在含有20个关键字的4阶B-树中进行查找，至多访问几个结点？

   4, 由$h=\lceil lo{g}_2(n+1)\rceil h=\; \backslash lceil\; log\_2\; (n+1)\backslash rceil$ 解得树高为5，又B-树所有叶结点在同一层，所以树高为4。

10. 将30个记录分为5块，进行分块查找，平均查找长度是13/2

    $ASL=\frac{b+1}{2}+\frac{s+1}{2}ASL\; =\; \backslash frac\{b+1\}\{2\}\; +\; \backslash frac\{s+1\}\{2\}$, 其中b为块数，s为每块记录数。

11. 判断：即使有向无环图的拓扑序列唯一，也不能唯一确定该图

    正确

12. 判断：简单选择排序在最好的情况下的时间复杂度度为O(n)

    错误，

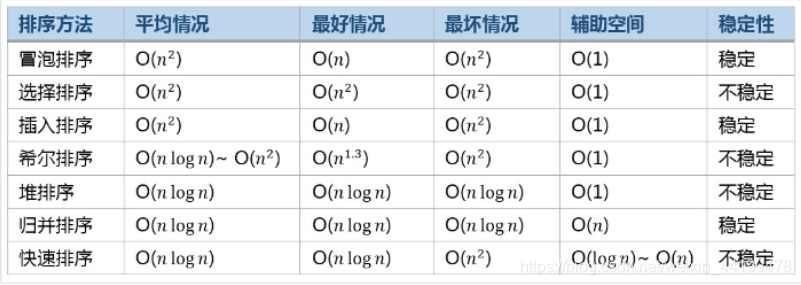
13. 不受待排序初始序列的影响，时间复杂度为$O(n^2)O(n^2)$的排序算法是简单选择排序。
14. 以下与数据结构无关的术语是___ A.树 B.顺序表 C.哈希表 D.链队列

    A

15. 用邻接矩阵A表示图，判定任意两个顶点$V_{i}V\_i$和$V_{j}V\_j$之间是否有长度为$nn$的路径相连，则只要检查_____的第i行第j列的元素是否为零即可。

    $A^{n-1}A^\{n-1\}$

16. 判断：若X是中序线索二叉树中一个有右孩子的结点，且X不为根，则X的后继为X的右子树中最左叶子结点。

    错误，是最左结点，不一定是叶子结点。

17. 已知三对角阵[1...9, 1...9]的每个元素2个存储单元，现将其三对角线上的元素以列序为主序存储在其实地址为1000的连续的内存单元中，则元素A[7,8]的地址____。

    $(7\times 3-1+1-1)\times 2=140(7\backslash times3-1+1-1)\backslash times2=140$

18. 求最短路径的 Dijkstra 算法的时间复杂度为？

    $O(\mathrm{\mid }{V}^2\mathrm{\mid })O(|V^2|)$

19. 顺序表中插入一个元素，需要平均移动的元素个数为几个？

    n/2, 长度为n的顺序表有n+1个插入位置，第一个移动n,第二个移动n-1,..., 以此类推，$\mathrm{总}\mathrm{移}\mathrm{动}=n+\mathrm{.}\mathrm{.}\mathrm{.}+2+1+0=\frac{n(n+1)}{2}总移动=n+...+2+1+0=\backslash frac\{n(n+1)\}\{2\}$, 因此平均移动的元素个数为$\frac{\frac{n(n+1)}{2}}{(n+1)}=\frac{n}{2}\backslash frac\{\backslash frac\{n(n+1)\}\{2\}\}\{(n+1)\}\; =\; \backslash frac\{n\}\{2\}$

20. 当各边上的权值______时，BFS算法可以用来解决单源最短路径问题

    相等

21. 所谓前缀编码是指在所有对字符编码中任何一个字符都不是________。

    另一个字符编码的前缀

22. 二叉树在线索化后，仍不能有效的解决什么问题?

    先序线索二叉树中求先序前驱、后续线索二叉树中求后序后继。

23. 利用栈求表达式23+34*5/7+108/9的值，操作数栈的大小至少为？

    4

24. 数据结构是一门研究______计算的程序设计问题中计算机的操作对象以及它们之间的关系。

    非数值

25. 根据n个元素建立一颗二叉排序树的时间复杂度为?

    $O(nlo{g}_{2}n)O(nlog\_2n)$

26. 在循环队列中，front指向队列中第一个元素的第一个位置，rear指向实际的队尾元素，队列满时的条件是？

    $front==(rear+1)\mathrm{\%}mfront\; ==\; (rear\; +\; 1)\backslash \%m$

27. 将两个各有n个元素的有序表归并成一个有序表，最少需要比较几次？

    n

28. 若线性表最常见的操作是存取第i个元素及其直接前驱的值，则采用哪种存储结构是最节省时间?

    顺序表

29. 判断:不论线性表采用顺序存储还是链式存储结构，删除值为X的结点时间复杂度均为$O(n)O(n)$？

    正确

30. 线索二叉树是一种____结构。

    物理

31. 栈和队列都是____结构，二叉树是____结构

    线性，树状

32. 动态查找表和静态查找表的重要区别在于前者包含有____和_____运算，而后者不包含这两种运算。

    插入；删除

33. 若不考虑基数排序，则在排序过程中，主要进行的两种基本操作是关键字的____和记录的_____。

    比较；移动

34. 文件由____组成；记录由____组成。

    记录；数据项

35. 一个深度为K， 具有最少结点数的完全二叉树按层次，(同层次从左到右)用自然数依次对结点编号，则编号最小的叶子的序号是_____。

    $2^{k-2}+12^\{k-2\}\; +\; 1$

36. 可以唯一的标识一个记录的关键字称为____。

    主关键字

37. 下面最适于表示稀疏无向图的是_____。 A. 邻接矩阵 B.逆邻接表 C.邻接多重表 D.十字链表

    C

38. 关键字序列用快速排序法进行排序时，速度最快的情形是?

    一般默认选择第一个元素为pivot, pivot在第一趟排序后越靠近中间，即左右两个子序列长度越接近，排序速度越快。

39. 循环单链表的最大优点是？

    任意结点出发可以访问到链接中每一个元素。

40. 两个栈共享空间时栈满的条件是_____。

    两个栈顶指针值相减的绝对值为1

算法总结

链表

1. （2002、2019-2）设计一个算法，在带头结点单链表中删去数据元素的值相同的多余结点，形成一个没有重复值得单链表。

    void deleteSame(LinkList *head){
       LNode *pre=head, *p=head->next;
       while(pre) {
           LNode *t=pre; //初始待删除结点的前驱结点
           while(p) { //寻找与pre指针所指元素相同的待删除结点
                if(pre->data == p->data) {//相同则删除
                    t->next = p->next;
                    free(p);
                    p = t->next; //继续后移寻找
                } else {//没找着继续后移
                    t = p;
                    p = p->next;
                }
           }
           //p查找完一遍
           pre = pre->next;
           p = pre->next;//重新定位到待查结点的后一个
       }
   }
   

2. (2020-1) 已知带头结点的非空链表L，设计一个算法，在不额外申请空间的条件下，将链表L中数值最小的结点移动到该链表的前端。

    void minFirst(LinkList *head) {
        LNode *p=head->next;
        LNode *m=p;//记录最小的结点
        LNode *mPre=head;//记录最小结点的前驱
        //寻找最小结点
        while(p->next) {
            if(p->data < p->next->data) {
                m = p->next;
                mPre = p;
            }else {
                p=p->next;
            }
        }
        //已找到最小结点
        minPre->next = m->next; //摘下最小
        //移动到头结点后
        m->next = head->next;
        head->next = m;
    }
   

3. (2020-2) 无头结点无头指针的循环单链表L， P指向任一结点，若P所指结点为奇数，则让P结点的前驱变为后继，若P所指结点为偶数，则让P的后继变为前驱。

   void exchange(LinkList *p) {
       LNode *c = p->next， *cPre = p;
       //寻找P的前驱，并记录p所在的位数
       while(c->next != p) {
           cPre = c;
           c = c->next;
       } 
       if(p->data%2==0) {//是偶数
           c->next = p->next;
           p->next = p->next->next;
           c->next->next = p; //将p的后继变为P的前驱
       }else{//是奇数
           cPre->next = p;
           p->next = c;
           c->next = p->next; //p的前驱结点变为后继
       }
   }
   

4. (2001) 设指针 head 指向无表头结点单链表的首结点。是设一算法，删除链表中的值为x的结点，若x结点不存在，则输出“不存在”信息。

   LinkList deleElem(LinkList *L, int x) {
       LNode c = new LNode();
       c->next = L;
       LNode *pre=c;
       int flag = 0;
       while(c) {
           if(c->data == x) { //删除当前结点
                flag++;
                pre->next = c->next;
                free(c);
                c = pre->next;
           } else {
               pre->next = c;
               c = c->next;
           }
       }
       if(flag == 0) {
           printf ("不存在");
           return L;
       }
       return c->next;
   }
   

5. (2003/2010) 假设循环单链表不空，且无表头结点亦无表头指针，指针p指向链表中某结点。请设计一个算法，将p所指结点的前驱结点变为p所指结点的后继结点。

   void exchange(CNode *p) {
       CNode *ppre=p, *pre=p->next;
       while(pre->next != p) { //找到P的前驱结点
           ppre = pre;
           pre = pre->next;
       }
       ppre->next = p;
       pre->next = p->next;
       p->next = pre;
   }
   

6. (2004)设计一个算法，对带表头结点的非空双向链表，用简单插入排序的方法，使其按结点从小到大链接。要求: 做结点的插入而不是交换数据域的值。

   void insertSort(DLinkList *head) {
       DNode *q=head;
       DNode *p=head->next->next;
       q->next->next = NULL; //断链
       DNode *r;
       while(p) {
            //取下当前结点
            r=p;
            p=p->next;//p县后移动
            r->next = NULL;//r摘下结点
            //插入q链表
            while(q->next) {
                if(r->data < q->next->data) {
                    //往前插
                    r->next = q->next;
                    q->next->prior = r;
                    q->next = r;
                    r->prior = q->next;
                    q = head; //重置q指针位置
                    break;
                } else{
                    if(q->next == NULL) {
                        q->next = r;
                        r->prior = q->next;
                        q = head; //重置q指针位置
                        break;
                    }else {
                        q = q->next;
                    }
                }
            }
       }
   }
   

7. (2007) 设有一个头指针为L的带有表头结点的非循环双向链表，其每个结点中有pred（前驱指针）、data（数据）和 next （后继指针）域外，要有一个访问频度域 freq。在链表被启用前其值均初始化为零。每当在链表中进行一次Locate（L, x），令元素为x的结点中 freq 域的值加一，并使链表中结点保持访问频度非递增的顺序排列，同时最近访问的结点排在相同频度的结点之后，以便使频繁访问的结点总是靠近表头。试编写Locate(L, x) 返回找到结点的地址，类型为指针型。

   DNode* Locate(DLinkList *L, ElemType x) {
       DNode *pre=L, *p=L->next;
       while(p) { //查找x所在的结点
           if(x == p->next) { //找到结点
               p->freq ++;
               pre->next = p->next;
               p->next->pred = pre; //摘下p结点
               //向前查找与 p 所指结点 freq 相同的结点
               while(pre) {
                   //查找到结点后把p链接到结点后
                   if(pre->freq == p->freq || pre == L) {
                       p->next = pre->next;
                       pre->next->pred = p;
                       p->pred = pre;
                       pre->next = p;
                       break;
                   }else {
                       pre = pre->pred;
                   }
               }
           }else {
               pre = p;
               p = p->next;
           }
       }
       return q;
   }
   

8. （2009）有一个带头结点的单链表，头指针为 head， 的数据域的类型为整型， 而且按自小到大的顺序排列， 编写一个算法 insertList(), 在该链表中插入值为x的元素，是该链表仍然有序。

   void insertList(LinkList *L, int x) {
        LNode *q = new LNode(x);
        LNode *p=L->next;
        if(p == NULL) L->next = x;
        while(p){
            if(x >= p->data || p->next == NULL) {
                x->next = p->next;
                p->next = x;
            }else {
                p = p->next;
            }
        }
   }
   

9. （2012/2018）两个整数序列 A=a1,a2, ... , am 和 B=b1,b2, ... ,bn 已经存入两个单链表中，设计一个算法，判断序列 B 是否是序列 A 的连续子序列。

   /**
   * 如果是返回 1， 不是返回 0 
   **/
   int isSubList(LinkList *A, LinkList *B) {
       LNode *pA=A, *preA=A; // 设A, B无头结点 
       LNode *pB=B; 
       while(pA) {
           if(pA->data == pB->data) {
               pA = pA->next;
               pB = pB->next;
           }else {
               preA = preA->next
               pA = preA;
               pB = B;
           }
           if(pB == NULL) return 1;
       }
       return 0;
   }
   

10. （2013）已知不带头结点的线性链表 list, 链表中结点构造为 （data, link），其中 data 为数据域，link 为指针域。请写一个算法，将该链表按结点数据域的值得大小从小到大重新链接。要求链接过程中不得使用除该链表以外的任何链结点空间。

    void resort(LinkList *L) {
        LNode *pre=L, *p=L->next;
        while(p) {
            LNode *preQ=pre, *q=p;
            while(q) {
                if(q->data < p->data) {
                    preQ->next = q->next; // 把q摘下
                    // 连接到p的前面
                    pre->next = q;  
                    q->next = p;
                } else {
                    preQ = q;
                    q = q->next;
                }
            }
            pre = p;
            p = p->next;
        }
    }
    

11. （2015）已知两个带头结点的单链表A和B，其头指针分别为 headA 和 headB, 编写一个算法从单链表 A 中删除自第i个元素起的共len个元素，然后将单链表 A 插入到单链表 B 中第j个元素之前。

    LinkList delInsert (LinkList *headA, LinkList *headB, int i, int j, int len) {
        LNode *preA=headA, *pA=headA->next;
        LNode *preB=headB, *pB=headB->next;
        int k=0;
        while(pA!=NULL && k < i) { // 找到A中第i个元素
            k++;
            preA = pA;
            pA = pA->next;
        }
        if(pA == NULL) {
            printf("给定i值不合法"); return headB;
        }
        k=0;
        while(pA!=NULL && k<len) { //找到A中第i+len个元素
            k++;
            pA = pA->next;
        }
        if(pA == NULL) {
            printf("给定len值不合法"); return headB;
        }
        LNode *t = preA->next;
        preA->next = pA->next;
        while(t != preA->next) { //施放删除的结点
            pA=t->next;
            free(t);
            t=pA;
        }
        k=0;
        while(pB!=NULL && k < j) {//找到B中第j个元素
            k++;
            preB=pB;
            pB=pB->next;
        }
        if(pB == NULL) {
            printf("给定j值不合法"); return headB;
        }
        //将A插入B
        PreB->next = headA;
        while(pA->next) { //找到A的最后一个结点
            preA = preA->next;
        } 
        preA->next = pB;
        return headB;
    }
    

12. (2016/期末9) 已知两个带头结点的按元素值递增次序排列的单链表A和B， 请编写算法将这两个单链表归并为一个按元素值非递增次序排列的单链表，并要求利用原来两个单链表的结点存放归并后的单链表。

    LinkList MergeList(LinkList *A, LinkList *B) {
        LNode c = A;
        LNode *pA=A->next;
        LNode *pB=B->next;
        LNode *t;
        while(pA != NUll || pB != NULL) { //先合并公共长度
            if(pA->data > pB->data) {
                t=pA->next;
                pA->next = c->next;
                c->next = pA;
                pA = t;
            } else {
                t=pB->next;
                pB->next = c->next;
                c->next = pB;
                pB = t;
            }
        }
        if(pA == NULL) { //剩下的头插入链表
            while(pB) {
                t=pB->next;
                pB->next = c->next;
                c->next = pB;
                pB = t;
            }
        } else if(PB == NULL) { // 剩下的头插入链表
             while(pA) {
                t=pA->next;
                pA->next = c->next;
                c->next = pA;
                pA = t;
            }
        } 
        return c;
    }
    

13. 已知一个不带头节点的双向循环链表（H为指向第一个结点的指针），从第二个结点至表尾递增有序。试编写程序，将第一个结点删除并插入表中适当位置，是整个链表递增有序， （设第二个数据域的值<第一个结点数据域的值<表尾数据域的值）。

    DLinkList resortList(DLinkList *H) {
        //初始化头结点
        DNode c = new DNode();
        //摘下第一个结点
        c->next = H->next;
        H->next->prior = c;
        //定义指针
        DNode *p = c;
        while(p->next) {
            if(H->data < p->next) { //找到第一个比H值大的结点插入
                H->next = p->next;
                p->next->prior = H;
                H->prior = p;
                p->next = H;
                break;
            } else if(!p->next) { //整个链表都没有比H值大的结点
                p->next = H;
                H->prior = p;
                break;
            } else { // 后移
                p = p->next;
            }
        }
        return c->next;
    }
    

14. (2019-1) 设有一个不带头结点的单循环链表L，其结点有3个域：data，next，prior 其中 data 为数据域：next为指针域，他指向后继结点：prior为指针域，他的值为空指针（NULL）。试编写一个将此单循环链表改成双向循环链表的算法。

    void stoDouble(DLinkList *L) {
        while(L->next) {
            L->next->prior = L;
            L = L->next;
        }
    }
    

15. 长度为n的字符串存储在结点大小为1的单链表中。试写一算法，判断字符串是否中心对称。

    
    int isSym(LinkList *L, int n) {
        int ans = n/2;
        LNode *p = L->next;
        char[] chars = new char[ans];
        for(int i=0; i< ans ; i++) {
            chars[i] = p->data;
            p = p->next;
        }
        if(ans%2!=0) p=p->next;
        while(p!=NULL && ans > 0) {
            if(p->data != chars[--ans])  {
                return 0;
            }
            p = p->next;
        }
        if(p ==NULL || ans == -1) {
            return 0
        }
        return 1;
    }
    

16. (2001) 已知一个二叉树存储与二叉链表中，其结点结构为[ lchild| data | rchild ]。其中 lchild 和 rchild 分别指向左子树和右子树根的指针域。试编写一个非递归算法，求二叉树的结点总数及其深度。

    void count_depth_tree(TreeNode *bt, int *depth, int *count) {
        TreeNode[] queue = new TreeNode[MAXSIZE];
        int front=0, rear=0;
        int last=1;
        //存第一个结点
        queue[rear++] = bt; ans++;
        while(front < rear) {
            TreeNode *t = queue[front++];
            count++;
            if(t->lchild) {
                queue[rear++] = t->lchild;
            }
            if(t->rchild) {
                queue[rear++] = t->rchild;
            }
            if(front == last) {
                depth++;
                last = rear;   
            }
        }
    }
    

17. （2002）将二叉树的结点按层一次编号（从根开始往下，同层自左向右）。请设计一个算法，将该二叉树的结点按编号从小到大顺序输出。设二叉树用二叉链表表示。

    void levelOrderTraversal(BiNode *T) {
        BiNode[] *queue = new BiNode[MAXSIZE];
        int front=0, rear=0;
        queue[rear++] = T;
        BiNode *t;
        while(front < rear) {
            t = queue[front++];
            printf("%d ",t->data);
            if(t->lchild) queue[rear++] = t->lchild;
            if(t->rchild) queue[rear++] = t->rchild;
        }
    }
    

18. （2003）请写出将二叉树中所有结点的左右子树相互交换的非递归算法。

    void reverseChild(BiNode *T) {
        BiNode[] *queue = new BiNode[MAXSIZE];
        int front=0, rear=0;
        queue[rear++] = T;
        BiNode *t1;
        BiNode *t2;
        while(front < rear) {
            t1 = queue[front++];
            t2 = t1->lchild;
            t1->lchild = t1->rchild;
            t1->rchild = t2;
            if(t1->rchild) queue[rear++] = t1->rchild;
            if(t1->lchild) queue[rear++] = t1->lchild;
        }
    }