描述
题目描述
给定我们一个数组,然后一个总和,让我们找到一个区间,满足区间的和大于等于这个总和,输出区间的长度,如果没有的话,我们可以直接输出
样例解释
样例输入
[1,2,4,4,1,1,1],9
这个满足总和相加大于等于的最短区间,我们可以选择,他们长度一样所以最后输出
3
题解
解法一:双指针维护窗口
实现思路
首先我们有两个指针,分别指向我们这个窗口的左右边界,我们的右指针每次向外扩展我们的这个窗口,然后每次,我们判断如果左指针可以收缩,我们一直让左指针收缩,这样我们最后得到的就是满足条件的了,最后我们每次求取出我们的最小值即可
图解代码
假设我们现在左指针和右指针的位置已经是这样了,然后我们判断,如果右指针向前移动一位,这个区间内是否总和还是大于等我们给定的那个值
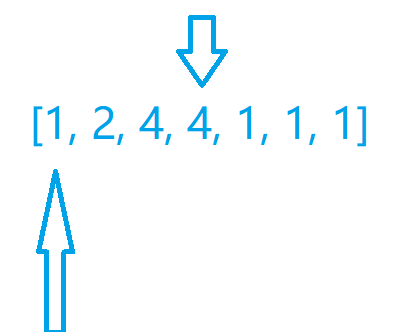
这里我们发现可以移动右指针,我们移动右指针
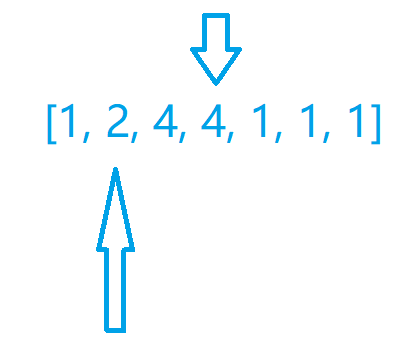
然后我们可以发现,我们现在的最小值是
然后我们继续移动左指针
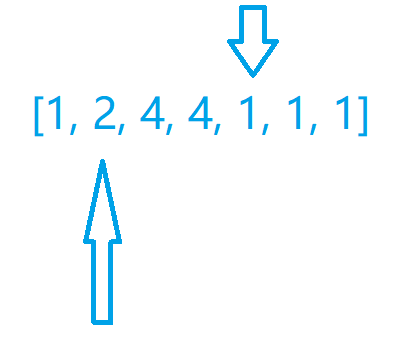
然后我们可以发现,我们可以继续移动右指针
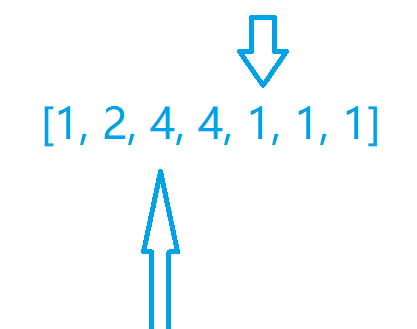
最小值还是,之后的也是以此类推,然后我们就可以得到我们的最小值
代码实现
class Solution {
public:
int minSubarray(vector<int>& nums, int target) {
int l = 0, r = 0, sum = 0, length = INT_MAX;
// 左边界,有边界,总和,长度
while (r < nums.size()) {
// 如果没遍历完我们的数组
sum += nums[r];
// 我们先扩展
while (sum - nums[l] >= target) sum -= nums[l++];
// 收缩我们的窗口
if (sum >= target) length = min(length, r - l + 1);
// 求取最小值
++r;
}
return length == INT_MAX ? 0 : length;
// 判断是否成立
}
};
时空复杂度分析
时间复杂度:
理由如下:我们左右指针无交叉,我们只是简单的扫描了一遍数组,所以我们的复杂度只是遍历一次数组
空间复杂度:
理由如下:我们只是引用了常数级别的变量空间
解法二:二分 + 前缀和
解题思路
首先我们可以从题目中的要求,要求一个子数组的总和要大于某一个值,那么我们快速求取某一段区间的区间和,可以考虑使用我们的前缀和数组,然后我们可以发现,这整个数组都是正整数,那么我们就可以保证我们的前缀和数组是单调递增的,这时候我们要对单调性有一个敏感度,看到单调性,我们可以考虑二分,考虑到了二分之后,我们想怎么去二分,有什么办法
这里因为我们已经判断出来了我们的前缀和数组是单调递增的,所以这里我们考虑一下在前缀和数组上做一下文章,我们想一下如何利用前缀和数组的单调性来分,我们可以很容易的想到,假设我们对前缀和数组的第位进行考虑,想要满足题目中条件一段区间和大于一个值,我们可以将我们当前的前缀和数组的第位加上这个值,然后我们在我们的前缀和数组中去寻找是否有大于等于这个值的出现,因为我们的前缀和数组是单调递增的,所以我们是可以直接整个数组去判断的,如果可以找到大于我们前缀和数组的第位加上我们的目标值的位置,我们就知道了我们子数组的结束位置,然后我们不断更新结束位置到起始位置的长度,就是我们最后子数组的大小
还有另一种思路,留给读者朋友去思考实现,我们可以二分我们的答案长度,假设我们取一个中间值作为我们最后子数组的长度,然后我们去验证是否可行,如果可以,那么我们说明比这个长度小或者等于这个长度的也或许可以,如果验证过后发现不可以,说明我们当前取到的长度小了,我们要扩大我们的长度
以上就是常见的两种二分的思路,一个是正向的二分,另一个是我们可知我们的答案满足某种单调性的条件,我们去二分我们的答案,然后验证更改范围
代码实现
class Solution {
public:
int minSubarray(vector<int>& nums, int target) {
int n = nums.size(), minn = INT_MAX;
vector<int> sum(n + 1, 0);
// 前缀和数组
for (int i = 1; i <= n; i++) sum[i] = sum[i - 1] + nums[i - 1];
// 求出前缀和
for (int i = 0; i <= n; i++) {
int tar = target + sum[i];
// 对每一位的初始值进行改变
int pos = -1;
// 位置
if (lower_bound(sum.begin(), sum.end(), tar) != sum.end()) pos = lower_bound(sum.begin(), sum.end(), tar) - sum.begin();
// 如果可以找到第一个不小于tar的值,就是我们这个区间的和大于target,那么我们更新位置坐标
if (pos != -1) minn = min(minn, pos - i);
// 判断最小的坐标
}
return minn == INT_MAX ? 0 : minn;
// 返回我们的最小值
}
};
时空复杂度分析
时间复杂度:
理由如下:首先我们每次二分的时间复杂度是的,然后我们遍历我们的整个长度为的数组,时间是的,那么我们最后的时间复杂度就是的
空间复杂度:
理由如下:我们开辟了一个前缀和的数组,空间大小为我们原来数组的大小






 京公网安备 11010502036488号
京公网安备 11010502036488号