我的头

#include<bits/stdc++.h>
using namespace std;
#define INF 0x3f3f3f3f3f3f3f3f
#define rep(i,j,k) for (int i=j;i<=k;++i)
#define per(i,j,k) for (int i=j;i>=k;--i)
//#define mid (l+r>>1)
//#define ls x<<1
//#define rs x<<1|1
#define fi first
#define se second
#define int long long
#define endl '\n'
//int up=*max_element(a+1,a+n+1);
const int mod=1e9+7;
const double PI=acos(-1);
const double eps=1e-6;
const int N=1e5+5;
void solve(){
}
signed main(){
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	int t;cin>>t;
	while(t--) solve();
	return 0;
}

数学

数论

欧拉线性筛

const int M=1e7;
bool vis[M];
int p[N];
void get_prime(){
  for(int i=2;i<M;i++){
  	if(!vis[i]) p[++p[0]]=i;
  	for(int j=1;j<=p[0]&&i*p[j]<M;j++){
  		vis[i*p[j]]=1;
  		if(i%p[j]==0) break;
  	}
  }
}

质因数分解

vector<int> pri;//质因数集合,需要olxxs
void zysfj(int x){
  pri.clear();
  for(int i=1;p[i]<x;i++){
  	if(x%p[i]==0){
  		int tmp=p[i];
  		pri.push_back(tmp);
  		while(x%tmp==0) x/=tmp;
  	}
  }
  if(x>1) pri.push_back(x);
}

GCD，LCM

int gcd(int a,int b){
  int tmp;
  while(b!=0){
  	tmp=a%b;a=b;b=tmp;
  }
  return a;
}
int lcm(int x,int y){
  return x*y/gcd(x,y);
}

线性逆元

int tt[N],intt[N];
void init_inff(){
  tt[0]=intt[0]=1;
  tt[1]=intt[1]=1;
  for(int i=2;i<N;i++){
  	tt[i]=i;
  	intt[i]=(mod - mod / i) * intt[mod % i] % mod;
  }
  for(int i=2;i<N;i++){
  	tt[i]=tt[i-1]*tt[i]%mod;
  	intt[i]=intt[i-1]*intt[i]%mod;
  }
}

扩展欧几里得

int ex_gcd(int a,int b,int &x,int &y){//a*x+b*y=1
   if(b==0){x=1,y=0;return a;}
   int d=ex_gcd(b,a%b,x,y);
   int tmp=x;
   x=y;
   y=tmp-(a/b)*y;
   return d;
}

中国剩余定理（Chinese Remainder Theorem）

求解满足x=a[i](modm[i])的最小正整数x (其中m[i]需要两两互质）。 //需要ex_gcd()

int CRT(){//n为方程组数
   int Mi,xi,yi,d,ans=0,M=1;
   for(int i=1;i<=n;i++) M*=m[i];
   for(int i=1;i<=n;i++){
      Mi=M/m[i];
      //Mi*xi=1(modm[i])<=>Mi*xi+m[i]*yi=1
      d=ex_gcd(Mi,m[i],xi,yi);
      ans=(ans+Mi*xi*a[i])%M;
   }
   return (ans+M)%M;
}

扩展中国剩余定理（Extended Chinese Remainder Theorem）

//需要ex_gcd()

如果函数返回 -1，表示方程组无解 时间复杂度：O(nlogM)，其中 n 是同余方程的个数，M 是所有模数的乘积。

int EX_CRT(){
   int aa=b[1],rr=a[1],x,y;
   for(int i=2;i<=n;i++){
      int bb=b[i];
      int c=a[i]-rr;
      int d=ex_gcd(aa,bb,x,y);
      if(c%d) return -1;
      c=c/d, bb=bb/d;
      x=(x*c%bb+bb)%bb;
      int lcm=aa*bb;
      rr=(x*aa%lcm+rr)%lcm;
      aa=lcm;
   }
   return rr=0?aa:rr;
}

欧拉函数

·1.求正整数n的欧拉函数φ(n)

int phi(int x){
   int res=x;
   for(int i=2;i*i<=x;i++){
      if(x%i==0){
          res=res-res/i;
          while(x%i==0) x/=i;
      }
   }
   if(x>1) res=res-res/x;
   return res;
}

·2.欧拉函数的线性求法

在欧拉线性筛的基础上增加的功能，在求质数的同时计算欧拉函数。

int phi[N],p[N];
bool vis[N];
void lin_phi(){
   phi[1]=1;
   for(int i=2;i<=n;i++){
      if(!vis[i]) p[++p[0]]=i,phi[i]=i-1;//φ(p)=p-1
      for(int j=1;j<=p[0]&&i*p[j]<=n;j++){
          vis[i*p[j]]=1;
          if(i%p[j]==0){phi[i*p[j]]=phi[i]*p[j];break;}
          phi[i*p[j]]=phi[i]*(p[j]-1);
      }
   }
}

扩展欧拉函数/欧拉降幂(ex_eular)

求a**b(mod c)

//需要phi()和ksm()

int ex_eular(int a,string b,int c){//a**b(modc)
   int ans=0,phic=phi(c);
   bool flag=0;//标记b是否大于等于φ(c)
   for(int i=0;i<b.size();i++){
      ans=ans*10+(b[i]-'0');
      if(ans>=phic){ans%=phic;flag=true;}
   }
   if(flag) ans+=phic;  
   return ksm(a,ans,c);
}

组合数学

线性逆元，组合数

int tt[N],intt[N];
void init_inff(){
  tt[0]=intt[0]=1;
  tt[1]=intt[1]=1;
  for(int i=2;i<N;i++){
  	tt[i]=i;
  	intt[i]=(mod - mod / i) * intt[mod % i] % mod;
  }
  for(int i=2;i<N;i++){
  	tt[i]=tt[i-1]*tt[i]%mod;
  	intt[i]=intt[i-1]*intt[i]%mod;
  }
}
int C(int n,int m){
  if(n<0||m<0||m>n) return 0;
  return tt[n]*intt[m]%mod*intt[n-m]%mod;
}

Lacus定理

求C(n,m,mod)，即Lucas(n,m,mo)即可

int Lucas(int a,int b,int mo){
  if(b==0) return 1;
  return C(a%mo,b%mo)*Lucas(a/mo,b/mo,mo)%mo;
}

其他

快速幂

int ksm(int a,int b,int c){
  int ans=1;
  while(b){
     if(b&1) ans=(ans*a)%c;
     b>>=1;
     a=(a*a)%c;
  }
  return ans;
}

lowbit

int lowbit(int x){
  if(x == 0)return 1e9;
  return x & (-x);
}

求二进制数中1的个数

int count1(int n){
   int cnt=0;while(n){
       n-=lowbit(n);
       cnt++;
   }
   return cnt;
}

复数

struct Complex{
  double x,y;
  Complex operator + (const Complex &w) const &{return (Complex){x+w.x,y+w.y};}
  Complex operator - (const Complex &w) const &{return (Complex){x-w.x,y-w.y};}
  Complex operator * (const Complex &w) const &{return (Complex){x*w.x-y*w.y,x*w.y+y*w.x};}
};

FFT

给定一个 $n$ 次多项式 $F(x)$ ，和一个 $m$ 次多项式 $G(x)$ 。

请求出 $F(x)$ 和 $G(x)$ 的乘积。

(保证输入中的系数大于等于 $0$ 且小于等于 $9$ , $1 \le n, m \leq {10}^6$ )

const int N=4e6+5;
struct comp{
   double x,y;
   comp operator+(const comp& t)const{return {x+t.x, y+t.y};}
   comp operator-(const comp& t)const{return {x-t.x, y-t.y};}
   comp operator*(const comp& t)const{return {x*t.x-y*t.y, x*t.y+y*t.x};}
}a[N],b[N];
int r[N],n,m;
void FFT(comp a[],int n,int op){
   for(int i=0;i<n;i++)//位逆序变换
       r[i]=(r[i>>1]>>1)+((i&1)?(n>>1):0);
   for(int i=0;i<n;i++)
       if(i<r[i]) swap(a[i],a[r[i]]);
   for(int i=2;i<=n;i<<=1){
       comp w1({cos(2*PI/i),sin(2*PI/i)*op});
       for(int j=0;j<n;j+=i){
           comp wk({1,0});
           for(int k=j;k<j+i/2;k++){
               comp x=a[k],y=a[k+i/2]*wk;
               a[k]=x+y;
               a[k+i/2]=x-y;
               wk=wk*w1;
           }
       }
   }
}
signed main(){
   ios::sync_with_stdio(false);
   cin.tie(nullptr);
   cin>>n>>m;
   for(int i=0;i<=n;i++) cin>>a[i].x;
   for(int i=0;i<=m;i++) cin>>b[i].x;
   for(m=n+m,n=1;n<=m;n<<=1);
   FFT(a,n,1);     FFT(b,n,1);
   for(int i=0;i<n;i++) a[i]=a[i]*b[i];
   FFT(a,n,-1);
   for(int i=0;i<=m;i++) cout<<(int)(a[i].x/n+0.5)<<" ";
}

二维坐标映射

//m为列数
int encode(int x,int y){return (x-1)*m+y;}
pair<int,int> decode(int id){return {(id-1)/m+1,(id-1)%m+1};}
//auto [x,y]=decode(id);

矩阵，矩阵快速幂

//const int msiz=;
//int siz=1e2;
struct matrix{int m[msiz+1][msiz+1];};
matrix operator *(const matrix& a,const matrix& b){//广义乘法运算（可自定义）
  matrix c;memset(c.m,0,sizeof(c.m));
  rep(i,1,siz)rep(j,1,siz)rep(k,1,siz)
     c.m[i][j]=(a.m[i][k]*b.m[k][j]+c.m[i][j])%mod;
  return c;
}
matrix ksm(matrix a,int k){
  matrix ans=a;
  k--;
  while(k){
     if(k&1) ans=ans*a;
     a=a*a;k>>=1;
  }
  return ans;
}

高斯消元

P2455 [SDOI2006] 线性方程组

题目描述

已知 $n$ 元线性一次方程组。

$\begin{cases} a_{1, 1} x_1 + a_{1, 2} x_2 + \cdots + a_{1, n} x_n = b_1 \\ a_{2, 1} x_1 + a_{2, 2} x_2 + \cdots + a_{2, n} x_n = b_2 \\ \cdots \\ a_{n,1} x_1 + a_{n, 2} x_2 + \cdots + a_{n, n} x_n = b_n \end{cases}$

请根据输入的数据，编程输出方程组的解的情况。

输入格式

第一行输入未知数的个数 $n$ 。
接下来 $n$ 行，每行 $n + 1$ 个整数，表示每一个方程的系数及方程右边的值。

输出格式

如果有唯一解，则输出解。你的结果被认为正确，当且仅当对于每一个 $x_i$ 而言结果值与标准答案值的绝对误差或者相对误差不超过 $0.01$ 。

如果方程组无解输出 $-1$ ；如果有无穷多实数解，输出 $0$ ；

输入 #1

输出 #1

x1=1.00
x2=0.00
x3=-1.00

【数据范围】
对于 $100\%$ 的数据， $1 \le n \le 50$ 。对于 $\forall 1\le i, j \le n$ ，有 $|a_{i, j}| \le 100$ ， $|b_i| \le 300$ 。

#include<bits/stdc++.h>
using namespace std;
const double eps=1e-6;
const int N=1e2+5;
int n,m;
double a[N][N];
int gauss(int n,int m){//n行m+1列的增广矩阵:a[0..n-1][0..n]
   int r=0;//r:有效方程数(矩阵的秩),操作时的行下标
   for(int c=0;c<m;++c){//遍历列 c:列下标
   	int t=r;
   	for(int i=r;i<n;++i)//寻找列主元
     		if(fabs(a[i][c])>fabs(a[t][c]))
         		t=i;
   	if(fabs(a[t][c])<eps) continue;//若主元列为0，不考虑，当前全列为0
   	//交换列主元t行与当前r行的数
   	for(int j=c;j<=m;j++) swap(a[t][j],a[r][j]);
   	for(int j=m;j>=c;j--) a[r][j]/=a[r][c];//使得主对角线系数均为1
   	for(int i=r+1;i<n;i++)//与r+1~n-1进行消元
   		if(fabs(a[i][c])>eps)
        		for(int j=m;j>=c;j--)
             		a[i][j]-=a[r][j]*a[i][c];
  	 	++r;             
   }
   for(int i=r;i<n;i++)
   	if(fabs(a[i][m])>eps)
     		return 2;//无解
   if(r<m) return 1;//无穷多解    
   for(int i=m-1;i>=0;i--)//回代求解方程
   	for(int j=i+1;j<m;j++)
     		a[i][m]-=a[j][m]*a[i][j];
   return 0;//一般情况(有唯一确定解）             
}
signed main(){
   cin>>n;
   for(int i=0;i<n;i++)
   for(int j=0;j<=n;j++)
     cin>>a[i][j];
   int flag=gauss(n,n);
   if(flag==1) cout<<0;
   else if(flag==2) cout<<-1; 
   else for(int i=0;i<n;i++) printf("x%d=%.2lf\n",i+1,a[i][n]);
}

容斥原理

/*问题:给定n和m个质数p1,p2...pm
求1~n中能被p1,p2...pm中至少一个数整除的数有多少个
m<=16,n,pi<=1e9*/
const int N=20;
int n,m,p[N];
int rongchi(int m){
   int res=0;
   for(int i=1;i<(1<<m);i++){
       int tmp=1,sign=-1;
       for(int j=0;j<m;j++)
           if(i&(1<<j)){
               if(tmp*p[j]>n){tmp=0;break;}
               tmp*=p[j];
               sign=-sign;
           } 
       if(tmp) res+=n/tmp*sign;
   }
   return res;
}
signed main(){
   ios::sync_with_stdio(false);
   cin.tie(0);
   cin>>n>>m;
   for(int i=0;i<m;i++) cin>>p[i];
   cout<<rongchi(m);
   return 0;
}

拉格朗日插值公式

const int mod=998244353;
const int N=2e3+5;
int ksm(int a,int b,int c){
  int ans=1;
  while(b){
     if(b&1) ans=(ans*a)%c;
     b>>=1;a=(a*a)%c;}
  return ans;
}
int n,k,ans=0;
int x[N],y[N];
signed main(){
  ios::sync_with_stdio(false);
  cin.tie(nullptr);
  cin>>n>>k;
  rep(i,1,n) cin>>x[i]>>y[i];
  rep(i,1,n){
  	int fz=y[i],fm=1;
  	rep(j,1,n){
  		if(i==j) continue;
  		fz=fz*(k-x[j]+mod)%mod;
  		fm=fm*(x[i]-x[j]+mod)%mod;
  	}
  	ans=(ans+(fz*ksm(fm,mod-2,mod))%mod)%mod;
  }
  cout<<ans<<endl;
  return 0;
}

动态规划

四边形不等式优化

//四边形不等式优化
//f[i][j]:区间[i,j]的石子合并的最小代价
//p[i,j]:记录每次循环后区间[i,j]的最优分割点
memset(f,0x3f,sizeof(3f));
cin>>n;
for(int i=1;i<=n;i++)
    cin>>a[i],s[i]=s[i-1]+a[i],f[i][i]=0,p[i][i]=i;
for(int len=2;len<=n;len++)
    for(int i=1,j;(j=len+i-1)<=n;i++)
        for(int k=p[i][j-1];k<=p[i+1][j];k++)
            if(f[i][j]>f[i][k]+f[k+1][j]+s[j]-s[i-1])
                f[i][j]=f[i][k]+f[k+1][j]+s[j]-s[i-1],p[i][j]=k;
cout<<f[1][n];

数位DP

int a[15]; 存储上界的每一位数字，方便dfs使用
int dp[]; 记忆化
int dfs(当前dp到的位置pos, dp的一些状态... , pos之前的所有数是否到达上界) {
...
}
//dp里只存pos及以后的位置不受上界a约束的情况数
//如果受到上界约束，pos位置能填的最大数字需要通过a确定，继续递归枚举下一位

P87654

$1$ 到 $N$ 中有多少个数满足其二进制表示中恰好有 $K$ 个 1

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=1e5+5;
int n,k,dp[100][100][2];
int a[100],len;
void init(int x){
  len=0;
  while(x>0){a[++len]=x%2;x>>=1;}
}
int dfs(int pos,int cnt,bool limit){
  if(pos<=0) return cnt==k;
  if(dp[pos][cnt][limit]!=-1) return dp[pos][cnt][limit];
  int res=0,up=limit?a[pos]:1;
  for(int i=0;i<=up;++i) res+=dfs(pos-1,cnt+(i==1),limit&&(i==up));
  dp[pos][cnt][limit]=res;
  return res;
}
signed main(){
  ios::sync_with_stdio(false);
  cin.tie(nullptr);
  memset(dp,-1,sizeof(dp));
  cin>>n>>k;
  init(n);
  cout<<dfs(len,0,1);
}

数列计数(春联3.1001)

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=1e5+5;
const int M=35,mod=998244353;
int n,a[N],l[N],s[M],jud[M],dp[M][2][2];
int len1,len2,len,ans;
int dfs(int pos,bool frt0,bool limit){
  if(pos<=0) return 1;
  if(dp[pos][frt0][limit]!=-1) return dp[pos][frt0][limit];
  int up=limit?s[pos]:1, res=0;
  for(int i=0;i<=up;i++){
  	if(frt0&&(i==0)){res+=dfs(pos-1,1,limit&&(i==up));continue;}
  	if(i<=jud[pos]) res+=dfs(pos-1,0,limit&&(i==up));
  }
  dp[pos][frt0][limit]=res;
  return res;
}
void init(int x,int A){
  memset(dp,-1,sizeof(dp));
  len1=0;
  while(x>0){s[++len1]=x%2;x>>=1;}
  len2=0;
  while(A>0){jud[++len2]=A%2;A>>=1;}
  ans*=dfs(len1,1,1);
  ans%=mod;
}
void solve(){
  cin>>n;
  for(int i=1;i<=n;i++) cin>>a[i];
  for(int i=1;i<=n;i++) cin>>l[i];
  ans=1;
  for(int i=1;i<=n;i++) init(min(a[i],l[i]),a[i]);
  cout<<ans<<endl;
}
signed main(){
  ios::sync_with_stdio(false);
  cin.tie(nullptr);
  int t;cin>>t;
  while(t--) solve();
}

数据结构

堆（题目）

在代码中，如果堆q在某个步骤变成了空，而之后又执行q.top()，这会导致问题，比如未定义的行为，进而导致程序崩溃或无法继续运行，从而卡死。

P1168 中位数

通过维护一个大根堆、一个小根堆的保持可以直接查询到中位数。

对于2i+1个数，大根堆存排序后前i个数，小根堆存排序后后i+1个数。

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=10e5+5;
int a[N];
priority_queue<int>Mq;
priority_queue<int,vector<int>,greater<int>>mq;
signed main(){
  ios::sync_with_stdio(false);
  cin.tie(0),cout.tie(0);
  int n;
  cin>>n;
  for(int i=1;i<=n;i++){
  	cin>>a[i];
  	if(i==1){
  		mq.push(a[i]);
  		cout<<a[1]<<endl;
  		continue;
  	}
  	if(i%2==0){//偶数 
  		if(a[i]>=mq.top()){
  			Mq.push(mq.top());
  			mq.pop();
  			mq.push(a[i]);
  		} 
  		else Mq.push(a[i]);
  	}
  	if(i%2==1){//奇数 
  		if(a[i]>=Mq.top())
  			mq.push(a[i]);
  		else{
  			mq.push(Mq.top());
  			Mq.pop();
  			Mq.push(a[i]);
  		}
  		cout<<mq.top()<<endl;
  	}
  }
}

线段树1

int n,m,a[N],op,x,y,k;
struct node{
    int sum,lazy=0;
}t[N<<2];
void build(int x,int l,int r){
    if(l==r){t[x].sum=a[l];return;}
    build(x<<1,l,mid);
    build(x<<1|1,mid+1,r);
    t[x].sum=t[x<<1].sum+t[x<<1|1].sum;
}
void down(int x,int l,int r){
    if(t[x].lazy){
       t[x<<1].sum+=t[x].lazy*(mid-l+1);
       t[x<<1].lazy+=t[x].lazy;
       t[x<<1|1].sum+=t[x].lazy*(r-mid);
       t[x<<1|1].lazy+=t[x].lazy;
       t[x].lazy=0;
    } 
}
void update(int x,int l,int r,int L,int R,int k){
    if(L<=l&&r<=R){
       t[x].sum+=k*(r-l+1);
       t[x].lazy+=k;
       return;
    }
    down(x,l,r);
    if(L<=mid) update(x<<1,l,mid,L,R,k);
    if(mid+1<=R) update(x<<1|1,mid+1,r,L,R,k);
    t[x].sum=t[x<<1].sum+t[x<<1|1].sum;
}
int query(int x,int l,int r,int L,int R){
    if(L<=l&&r<=R) return t[x].sum;
    if(L>r||R<l) return 0;
    down(x,l,r);
    return query(x<<1,l,mid,L,R)+query(x<<1|1,mid+1,r,L,R);
}

线段树2

struct node{
	int sum,add,mul;
}t[N<<2];
int n,m,L,R,q,op,k,a[N];
void build(int x,int l,int r){
    if(l==r){t[x]={a[l],0,1};return;}
    build(x<<1,l,mid);
    build(x<<1|1,mid+1,r);
    t[x]={(t[x<<1].sum+t[x<<1|1].sum)%m,0,1};
}
void down(int x,int l,int r){
    if(t[x].mul!=1||t[x].add!=0){
       t[x<<1].sum=(t[x<<1].sum*t[x].mul+t[x].add*(mid-l+1))%m;
       t[x<<1|1].sum=(t[x<<1|1].sum*t[x].mul+t[x].add*(r-mid))%m;
       t[x<<1].mul=(t[x<<1].mul*t[x].mul)%m;
       t[x<<1|1].mul=(t[x<<1|1].mul*t[x].mul)%m;
       t[x<<1].add=(t[x<<1].add*t[x].mul+t[x].add)%m;
       t[x<<1|1].add=(t[x<<1|1].add*t[x].mul+t[x].add)%m;
       t[x].mul=1,t[x].add=0;
    }
}
void update_add(int x,int l,int r){
    if(L<=l&&r<=R){
       t[x].sum+=k*(r-l+1);
       t[x].sum%=m;
       t[x].add=(t[x].add+k)%m;
       return;
    }
    down(x,l,r);
    if(mid>=L) update_add(x<<1,l,mid);
    if(mid<R) update_add(x<<1|1,mid+1,r);
    t[x].sum=(t[x<<1].sum+t[x<<1|1].sum)%m;
}
void update_mul(int x,int l,int r){
    if(L<=l&&r<=R){
       t[x].sum=t[x].sum*k%m;
       t[x].mul=(t[x].mul*k)%m;
       t[x].add=t[x].add*k%m;
       return;
    }
    down(x,l,r);
    if(mid>=L) update_mul(x<<1,l,mid);
    if(mid<R) update_mul(x<<1|1,mid+1,r);
    t[x].sum=(t[x<<1].sum+t[x<<1|1].sum)%m;
}
int query(int x,int l,int r){
    if(L<=l&&r<=R){return t[x].sum;}
    if(r<L||l>R){return 0;}
    down(x,l,r);
    return (query(x<<1,l,mid)+query(x<<1|1,mid+1,r))%m;
}

(线段树)区间最大子段和 [P4513 小白逛公园]

P4513 小白逛公园

输入格式

第一行，两个整数 $n$ 和 $m$ ，分别表示表示公园的数量和操作（遛狗或者改变打分）总数。

接下来 $n$ 行，每行一个整数，依次给出小白开始时对公园的打分。

接下来 $m$ 行，每行三个整数。其中第一个整数 $k$ 为 $1$ 或 $2$ 。

$k=1$ ，接下来的两个整数 $a$ 和 $b$ 给出了选择公园的范围 $(1 \le a,b \le n)$ 。测试数据可能会出现 $a > b$ 的情况，需要进行交换；

$k=2$ ，接下来的两个整数 $p$ 和 $s$ ，表示小白对第 $p$ 个公园的打分变成了 $s(1\le p\le N)$ 。

输出格式

小白每出去玩一次，都对应输出一行，只包含一个整数，表示小白可以选出的公园得分和的最大值。

输入 #1
5 3
1
2
-3
4
5
1 2 3
2 2 -1
1 2 3
输出 #1
2
-1

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define mid ((l+r)>>1)
const int N=5e5+5;
int a[N];
struct node{    
  int sum,lm,rm,mx;
}t[N<<2];
int n,m,k,x,y,p=N<<2;
void push(node& x,const node& y,const node& z){
  x.sum=y.sum+z.sum;
  x.lm=max(y.lm , y.sum+z.lm);
  x.rm=max(y.rm+z.sum , z.rm);
  x.mx=max(y.rm+z.lm , max(y.mx,z.mx));
}
void build(int x,int l,int r){
  if(l==r){t[x]={a[l],a[l],a[l],a[l]};return;}
  build(x<<1,l,mid);
  build(x<<1|1,mid+1,r);
  push(t[x],t[x<<1],t[x<<1|1]);
}
void update(int pos,int s,int x,int l,int r){
  if(pos==l&&l==r){t[x]={s,s,s,s};return;}
  if(mid>=pos) update(pos,s,x<<1,l,mid);
  if(mid+1<=pos) update(pos,s,x<<1|1,mid+1,r);
  push(t[x],t[x<<1],t[x<<1|1]);
}
node query(int L,int R,int x,int l,int r){
  if(L<=l&&r<=R) return t[x];
  if(L<=mid&&mid+1<=R){
      node res;
      push(res,query(L,R,x<<1,l,mid),query(L,R,x<<1|1,mid+1,r));
      return res;
  }
  if(mid>=L) return query(L,R,x<<1,l,mid);
  if(mid<=R) return query(L,R,x<<1|1,mid+1,r);
}
signed main(){
  cin>>n>>m;
  for(int i=1;i<=n;i++) cin>>a[i];
  build(1,1,n);
  for(int i=1;i<=m;i++){
      cin>>k>>x>>y;
      if(k==1){
          if(x>y) swap(x,y);
          cout<<query(x,y,1,1,n).mx<<endl;
      }else{update(x,y,1,1,n);}
  }
}

并查集

并查集判断连通块个数

P1197 [JSOI2008] 星球大战
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=4e5+5;
int n,m,k,x,y,u,v,tot;
int ans[N],a[N],be[N],s[N];
vector<int> e[N]; 
int find(int x){
 return s[x]==x?x:s[x]=find(s[x]);
}
void merge(int x,int y){
 x=find(x);y=find(y);
 if(x!=y) s[x]=s[y];
}
signed main(){
 cin>>n>>m;
 for(int i=0;i<n;i++) s[i]=i;
 for(int i=1;i<=m;i++){
 	cin>>x>>y;
 	e[x].push_back(y);
 	e[y].push_back(x);
 }
 cin>>k;
 for(int i=1;i<=k;i++){
 	cin>>x;
 	a[i]=x;//记录被摧毁的星球 
 	be[x]=1;//标记x被摧毁 
 }
 tot=n-k;//剩余先独立成块 
 //判断两星球没被摧毁且没在同一个集合，则合并
 for(int u=0;u<n;u++)
 	for(int v:e[u]){
 		int x=find(u),y=find(v);
 		if(!be[u]&&!be[v]&&x!=y){
 			s[x]=s[y];
 			tot--;
 		}
 	}
 ans[k]=tot;//摧毁k个星球后的ans 
 for(int j=k-1;j>=0;j--){//逆向修复 
 	u=a[j+1];be[u]=0;
 	tot++;
 	for(int v:e[u]){
 //都没被摧毁并且在同一个集合，则合并 
 		x=find(u);y=find(v);
 		if(!be[v]&&x!=y){
 			s[x]=s[y];
 			tot--;
 		}
 	}
 	ans[j]=tot;
 }
 for(int i=0;i<=k;i++) cout<<ans[i]<<endl;
}
带权值并查集+二分图

P1525 [NOIP 2010 提高组] 关押罪犯
P1525 [NOIP 2010 提高组] 关押罪犯

题目背景

NOIP2010 提高组 T3

题目描述

S 城现有两座监狱，一共关押着 $N$ 名罪犯，编号分别为 $1\sim N$ 。他们之间的关系自然也极不和谐。很多罪犯之间甚至积怨已久，如果客观条件具备则随时可能爆发冲突。我们用“怨气值”（一个正整数值）来表示某两名罪犯之间的仇恨程度，怨气值越大，则这两名罪犯之间的积怨越多。如果两名怨气值为 $c$ 的罪犯被关押在同一监狱，他们俩之间会发生摩擦，并造成影响力为 $c$ 的冲突事件。

每年年末，警察局会将本年内监狱中的所有冲突事件按影响力从大到小排成一个列表，然后上报到 S 城 Z 市长那里。公务繁忙的 Z 市长只会去看列表中的第一个事件的影响力，如果影响很坏，他就会考虑撤换警察局长。

在详细考察了 $N$ 名罪犯间的矛盾关系后，警察局长觉得压力巨大。他准备将罪犯们在两座监狱内重新分配，以求产生的冲突事件影响力都较小，从而保住自己的乌纱帽。假设只要处于同一监狱内的某两个罪犯间有仇恨，那么他们一定会在每年的某个时候发生摩擦。

那么，应如何分配罪犯，才能使 Z 市长看到的那个冲突事件的影响力最小？这个最小值是多少？

输入格式

每行中两个数之间用一个空格隔开。第一行为两个正整数 $N,M$ ，分别表示罪犯的数目以及存在仇恨的罪犯对数。接下来的 $M$ 行每行为三个正整数 $a_j,b_j,c_j$ ，表示 $a_j$ 号和 $b_j$ 号罪犯之间存在仇恨，其怨气值为 $c_j$ 。数据保证 $1<a_j< b_j\leq N, 0 < c_j\leq 10^9$ ，且每对罪犯组合只出现一次。

输出格式

共一行，为 Z 市长看到的那个冲突事件的影响力。如果本年内监狱中未发生任何冲突事件，请输出 0。

输入输出样例 #1

输入 #1
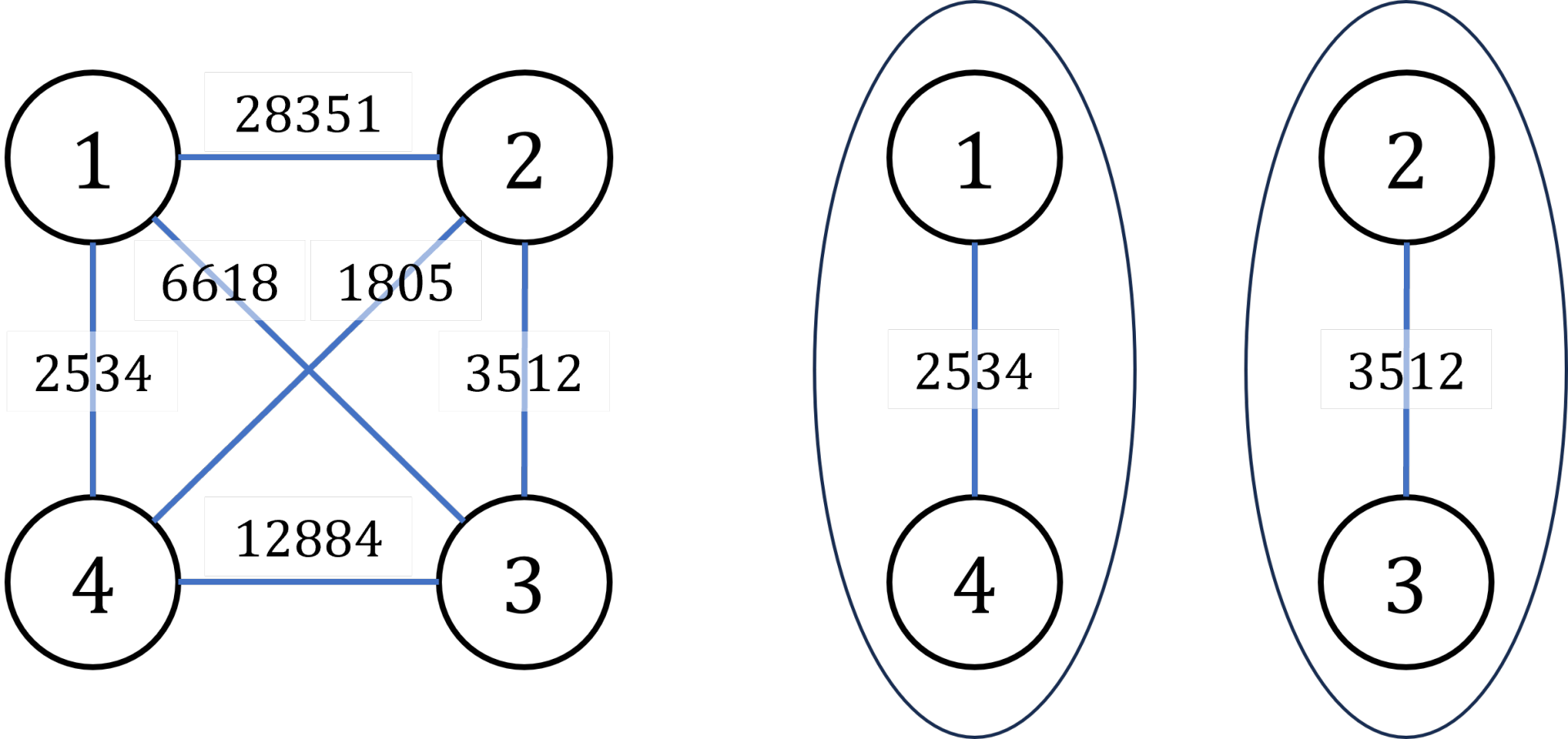
4 6
1 4 2534
2 3 3512
1 2 28351
1 3 6618
2 4 1805
3 4 12884
输出 #1
3512
说明/提示

输入输出样例说明

罪犯之间的怨气值如下面左图所示，右图所示为罪犯的分配方法，市长看到的冲突事件影响力是 $3512$ （由 $2$ 号和 $3$ 号罪犯引发）。其他任何分法都不会比这个分法更优。

数据范围

对于 $30\%$ 的数据有 $N\leq 15$ 。

对于 $70\%$ 的数据有 $N\leq 2000,M\leq 50000$ 。

对于 $100\%$ 的数据有 $N\leq 20000,M\leq 100000$ 。

题解：

淳朴的并查集~但因为它们带有权值，因此排序是必须的，我们要尽可能让危害大的罪犯在两个监狱里。

那么，再结合**敌人的敌人和自己在一个监狱的规律合并 ( 二分图思想 )**。

当查找时发现其中两个罪犯不可避免地碰撞到一起时，只能将其输出并结束。

还有一点很重要，就是没有冲突时一定输出0！！！
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int n,m,x,y,s[N];
int p[N];//将罪犯分为0,1两个阵营 
struct node{
 int x,y,z;
 bool operator<(const node&x)const{return z>x.z;}
}a[N];
int find(int x){
 return s[x]==x?x:s[x]=find(s[x]);
}
void merge(int x,int y){
 x=find(x),y=find(y);
 s[x]=y;
}
signed main(){
 ios::sync_with_stdio(false);
 cin.tie(0),cout.tie(0);
 cin>>n>>m;
 for(int i=1;i<=n;i++) s[i]=i; 
 for(int i=1;i<=m;i++)
 	cin>>a[i].x>>a[i].y>>a[i].z;
 sort(a+1,a+1+m);
 for(int i=1;i<=m;i++){
 	x=find(a[i].x),y=find(a[i].y);
 	if(x==y){cout<<a[i].z;return 0;}
 	else{
 		if(p[a[i].x]==0) p[a[i].x]=a[i].y;
 		else merge(a[i].y,p[a[i].x]);
 		if(p[a[i].y]==0) p[a[i].y]=a[i].x;
 		else merge(a[i].x,p[a[i].y]);
 	}
 }
 cout<<0;
}
种类并查集/扩展域并查集

引入

并查集能维护连通性、传递性，通俗地说，亲戚的亲戚是亲戚。

然而当我们需要维护一些对立关系，比如 敌人的敌人是朋友 时，正常的并查集就很难满足我们的需求。

这时，种类并查集就诞生了。

常见的做法是将原并查集扩大一倍规模，并划分为两个种类。

在同个种类的并查集中合并，和原始的并查集没什么区别，仍然表达他们是朋友这个含义。

考虑在不同种类的并查集中合并的意义，其实就表达 他们是敌人 这个含义了。

按照并查集美妙的 传递性，我们就能具体知道某两个元素到底是 敌人 还是 朋友 了。

至于某个元素到底属于两个种类中的哪一个，由于我们不清楚，因此两个种类我们都试试。

具体实现，详见 P1525 关押罪犯。

利用并查集本身‘连通性’表示’关系’，用‘坐标区间’表示‘属性’。

P1892 [BalticOI 2003] 团伙
Q:为什么是朋友的情况下不加上merge(x+n,y+n);

Ans(Devin):那句话翻译过来就是“两个朋友各自的敌人是不是需要变成朋友”。

把拓展域并查集理解成’虚拟节点‘：a的敌人a+n，但不知道具体是谁，但是后面把敌人都放到这个并查集里。
#include<bits/stdc++.h>
using namespace std;
const int N=3e5+5;
int s[N];
int n,m,ans;
int find(int x){return s[x]==x?x:s[x]=find(s[x]);}
void merge(int x,int y){s[find(y)]=find(x);}
signed main(){
 int x,y;
 string op;
 cin>>n>>m;
 for(int i=1;i<=n<<1;i++) s[i]=i;
 for(int i=1;i<=m;i++){
 	cin>>op>>x>>y;
 	if(op=="F"){merge(x,y);}
 	else{merge(x,y+n),merge(y,x+n);}
 }
 for(int i=1;i<=n;i++)
 	if(s[i]==i) ans++;
 cout<<ans;
}
P2024 [NOI2001] 食物链
P2024 [NOI2001] 食物链

题目描述

动物王国中有三类动物 $A,B,C$ ，这三类动物的食物链构成了有趣的环形。 $A$ 吃 $B$ ， $B$ 吃 $C$ ， $C$ 吃 $A$ 。

现有 $N$ 个动物，以 $1 \sim N$ 编号。每个动物都是 $A,B,C$ 中的一种，但是我们并不知道它到底是哪一种。

有人用两种说法对这 $N$ 个动物所构成的食物链关系进行描述：

第一种说法是 1 X Y，表示 $X$ 和 $Y$ 是同类。

第二种说法是2 X Y，表示 $X$ 吃 $Y$ 。

此人对 $N$ 个动物，用上述两种说法，一句接一句地说出 $K$ 句话，这 $K$ 句话有的是真的，有的是假的。当一句话满足下列三条之一时，这句话就是假话，否则就是真话。

当前的话与前面的某些真的话冲突，就是假话；

当前的话中 $X$ 或 $Y$ 比 $N$ 大，就是假话；

当前的话表示 $X$ 吃 $X$ ，就是假话。

你的任务是根据给定的 $N$ 和 $K$ 句话，输出假话的总数。

输入格式

第一行两个整数， $N,K$ ，表示有 $N$ 个动物， $K$ 句话。

第二行开始每行一句话（按照题目要求，见样例）

输出格式

一行，一个整数，表示假话的总数。

输入输出样例 #1

输入 #1
100 7
1 101 1
2 1 2
2 2 3
2 3 3
1 1 3
2 3 14
1 5 5
输出 #1
3
说明/提示

对于全部数据， $1\le N\le 5 \times 10^4$ ， $1\le K \le 10^5$ 。

题解：

概念解释

再来看本题，每个动物之间的关系就没上面那么简单了。

对于动物 x 和 y，我们可能有 x 吃 y，x 与 y 同类，x 被 y 吃。

但由于关系还是明显的，1 倍大小、2 倍大小的并查集都不能满足需求，3 倍大小不就行了！

类似上面，我们将并查集分为 3 个部分，每个部分代表着一种动物种类。

设我们有 n 个动物，开了 3n 大小的种类并查集，其中 1∼n 的部分为 A 群系，n+1∼2n 的部分为 B 群系，2n+1∼3n 的部分为 C 群系。

我们可以认为 A 表示中立者，B 表示生产者，C 表示消费者。此时关系明显：A 吃 B，A 被 C 吃。

当然，我们也可以认为 B 是中立者，这样 C 就成为了生产者，A 就表示消费者。（还有 1 种情况不提及了）

联想一下 2 倍大小并查集的做法，不难列举出：当 A 中的 x 与 B 中的 y 合并，有关系 x 吃 y；当 C 中的 x 和 C 中的 y 合并，有关系 x 和 y 同类等等……

但仍然注意了！我们不知道某个动物属于 A，B，还是 C，我们 3 个种类都要试试！

也就是说，每当有 1 句真话时，我们需要合并 3 组元素。

容易忽略的是，题目中指出若 x 吃 y，y 吃 z，应有 x 被 z 吃。

这个关系还能用种类并查集维护吗？答案是可以的。

若将 x 看作属于 A，则 y 属于 B，z 属于 C。最后，根据关系 A 被 C 吃可得 x 被 z 吃。

既然关系满足上述传递性，我们就能放心地使用种类并查集来维护啦。

一倍存本身，二倍存猎物，三倍存天敌

唯一容易忽略的点就是：一的猎物的猎物就是一的天敌 那么我们每次只要维护三个并查积的关系就可以了
#include<bits/stdc++.h>
using namespace std;
const int N=3e5+5;
int s[N];
int n,k,ans;
int find(int x){return s[x]==x?x:s[x]=find(s[x]);}
int merge(int x,int y){
  x=find(s[x]),y=find(s[y]);
  s[x]=y;
}
signed main(){//对于每种生物:设 x 为本身,x+n为猎物,x+2*n为天敌
  int x,y,op;
  cin>>n>>k;
  for(int i=1;i<=3*n;++i) s[i]=i;
  for(int i=1;i<=k;++i) {
      cin>>op>>x>>y;
      if(x>n||y>n){ans++;continue;}
      if(op==1){
          if(find(x+n)==find(y)||find(x+2*n)==find(y))//如果x是y的天敌或猎物
 			{ans++;continue;}
          merge(x,y);merge(x+n,y+n);merge(x+2*n,y+2*n);
      }
      else if(op==2){
          if(x==y) {ans++; continue;}
          if(find(x)==find(y)||find(x+2*n)==find(y))//如果1是2的同类或猎物
          	{ans++; continue;}
          merge(x,y+2*n);merge(x+n,y);merge(x+2*n,y+n);
          //x的同类是y的天敌,x的猎物是y的同类,x的天敌是y的猎物
      }
  }
  cout<<ans;
}
带权并查集

P1196 [NOI2002] 银河英雄传说
dist[i]:i到队列队头的距离. siz[i]:以i为队头的队列的元素个数.

如何计算每个飞船到队头的距离：对于任意一个飞船，我们都知道它的祖先（不一定是队头，但一定间接或直接指向队头），还知道距离它祖先的距离。对于每一个飞船，’它到队头的距离‘ = ’它到它祖先的距离‘ + ’它祖先到队头的距离‘，而它的祖先到队头的距离，也可以变成类似的。可以递归实现，由于每一次更新都要用到已经更新完成的祖先到队头的距离，所以要先递归找到队头，然后在回溯的时候更新（front[i]+=front[fa[i]]），可以把这个过程和查找队头的函数放在一起。
#include<bits/stdc++.h>
using namespace std;
const int N=3e4+5;
int s[N],dist[N];//dist[i]:i到队列队头的距离 
int siz[N];//siz[i]:以i为队头的队列的元素个数 
int find(int x){
 if(s[x]==x) return x;
 int root=find(s[x]);
 dist[x]+=dist[s[x]]; //?
 return s[x]=root;
}
signed main(){
 char op;
 int x,y,t;
cin>>t;
for(int i=1;i<N;i++) s[i]=i,siz[i]=1;
while(t--){
 	cin>>op>>x>>y;
 	if(op=='M'){
 		int xx=find(x),yy=find(y);
 		s[xx]=yy;//x接在y后面
 		dist[xx]+=siz[yy];
 		siz[yy]+=siz[xx];
 		siz[xx]=0;
 	}
 	else{
 		if(find(x)!=find(y)) cout<<-1<<endl;
 		else cout<<abs(dist[x]-dist[y])-1<<endl; 
 	}
 }
}
扩展域并查集不能维护边权。

倍增算法

倍增与ST表（题目）

时间复杂度

预处理go[] []数组: O(nlogn)

一次查询：O(logn)

预处理LOG2（如果嫌库函数log2()比较慢）

lg[i]的值与向下取整的log2(i)相等

查询量较大时，预处理LOG2[]较快
lg[1]=0;
for(int i=2;i<=N;i++) 
 lg[i]=lg[i>>1]+1;
用log2()函数时通过整数赋值可以省略floor
int k=log2(n);
for(int i=1;i<=k;i++){
 for(int s=1;s+(1<<k)-1<=n;s++){
 	......
 }
}

P4155 [SCOI2015] 国旗计划 (倍增思想)

1.化圆为线

2.贪心。问题等价于：选取最少的线段使得完全覆盖”数轴“。

对比题目：P1803线段覆盖（经典贪心）

共同点：对右端点进行排序，贪心放置。不同点：P1803是选择下一条左端点在该点右边（不重合）的点 P4155是选择一条重合部分最少的点。（就是排序后下一个不重合点的前一个）

贪心用来初始化go[s] [0]。

3.倍增法（查询）：go[s] [i]表示：从第s区间出发该选择的第2^i条线段（区间编号） 满足go[s] [i]=go[go[s] [i-1]] [i-1]； go数组属于预处理部分
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+5;
#define int long long
int n,m;
int res[N],go[2*N][20];//go[s][i]表示:s后第2**i的区间     2**20=1e6
struct node{
	int id,l,r;
	bool operator <(const node &x)const{return l<x.l;}
}w[2*N];
void init(){
	int nxt=1;
	for(int i=1;i<=2*n;i++){
		while(nxt<=2*n&&w[nxt].l<=w[i].r)
			nxt++;
		go[i][0]=nxt-1;
	}
	for(int i=1;(1<<i)<=n;i++)
		for(int s=1;s<=2*n-1;s++)
			go[s][i]=go[go[s][i-1]][i-1]; 
}
void sol(int x){
	int end=w[x].l+m,cur=x,ans=1;
	for(int i=log2(n);i>=0;i--){
		int pos=go[cur][i];
		if(pos==0 || w[pos].r>=end) continue;
		ans+=1<<i;
		cur=pos;
	}
	res[w[x].id]=ans+1;
}
signed main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		w[i].id=i;
		cin>>w[i].l>>w[i].r;
		if(w[i].r<w[i].l) w[i].r+=m;
	}
	sort(w+1,w+n+1);
	for(int i=1;i<=n;i++){
		w[i+n].id=w[i].id;
		w[i+n].l=w[i].l+m;
		w[i+n].r=w[i].r+m;
	}
	init();
	for(int i=1;i<=n;i++) sol(i);//排序后存储顺序变化
	for(int i=1;i<=n;i++) cout<<res[i]<<" "; 
}

P2880 [USACO07JAN] Balanced Lineup G （ST表）

法1：ST表

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=5e4+5;
int n,q,h[N],LOG2[N],st_max[N][21],st_min[N][21];
void st_init(){//此时ST表直接存值（不存下标） 
 LOG2[0]=-1;
 for(int i=1;i<=N;i++) LOG2[i]=LOG2[i>>1]+1;
 for(int i=1;i<=n;i++)//初始化长度为1的ST表 
 	st_max[i][0]=st_min[i][0]=h[i];
 for(int i=1;i<=LOG2[n];i++){
 	for(int s=1;s+(1<<i)-1<=n;s++){
 		int tmp=(1<<(i-1));
 		st_max[s][i]=max(st_max[s][i-1],st_max[s+tmp][i-1]);
 		st_min[s][i]=min(st_min[s][i-1],st_min[s+tmp][i-1]);
 	}
 }
}
int query(int l,int r){//将一段[l,r]拆成[l,l+(1<<k)]和[r-(1<<k)+1,r] 
 int k=LOG2[r-l+1];//k满足2**k<=len && 2**(k+1)>=len 
 int x=max(st_max[l][k],st_max[r-(1<<k)+1][k]);
 int y=min(st_min[l][k],st_min[r-(1<<k)+1][k]);
 return x-y;
}
signed main(){
 ios::sync_with_stdio(false);
 cin.tie(0),cout.tie(0);
 cin>>n>>q;
 for(int i=1;i<=n;i++) cin>>h[i];
 st_init();
 int a,b;
 for(int i=1;i<=q;i++){
 	cin>>a>>b;
 	cout<<query(a,b)<<endl;
 }
}

法2：线段树

#include<bits/stdc++.h>
using namespace std;
const int N=5e4+5;
#define int long long
#define mid ((l+r)>>1)
struct node{
 int l,r,M,m;
}t[N<<2];
int n,q,x,y,a[N];
void build(int x,int l,int r){
 if(l==r){t[x].M=t[x].m=a[l];return;}
 build(x<<1,l,mid);
 build(x<<1|1,mid+1,r);
 t[x].M=max(t[x<<1].M,t[x<<1|1].M);
 t[x].m=min(t[x<<1].m,t[x<<1|1].m);
}
int query_M(int L,int R,int x,int l,int r){
 if(L<=l&&r<=R) return t[x].M;
 if(L>r||R<l) return 1;
 return max(query_M(L,R,x<<1,l,mid),query_M(L,R,x<<1|1,mid+1,r));
}
int query_m(int L,int R,int x,int l,int r){
 if(L<=l&&r<=R) return t[x].m;
 if(L>r||R<l) return 1e7;
 return min(query_m(L,R,x<<1,l,mid),query_m(L,R,x<<1|1,mid+1,r));
}
signed main(){
 cin>>n>>q;
 for(int i=1;i<=n;i++) cin>>a[i];
 build(1,1,n);
 for(int i=1;i<=q;i++){
 	cin>>x>>y;
 	cout<<query_M(x,y,1,1,n)-query_m(x,y,1,1,n)<<endl;
 }
}

P5465 [PKUSC2018] 星际穿越

思路：

1.前缀和思想

2.贪心 + 倍增优化与**[SCOI2015]国旗计划**神似。

以往都是对ans直接进行倍增优化.本题对前缀和数组进行直接倍增优化。

具体转移：

f[i][j]:从i跳2^j步能到达的左端点。
状态转移方程：f[i][j]=f[f[i][j-1]][j-1]

g[i][j]:从i到[ f[i][j],i-1 ]区间上所有点的最小步数和
g[i][j]= g[i][j-1] + g[f[i][j-1][j-1]+(f[i][j-1]-f[i][j])*2^(j-1)

转移初始化：

关键：f[i] [0]=min(f[i+1] [0] , l[i]);

f[n][0]=l[n];g[n][0]=n-l[n];
for(int i=n-1;i>=2;i--){
 f[i][0]=min(f[i+1][0],l[i]);
 g[i][0]=i-f[i][0];
}

代码：

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=3e5+5;
int n,q,f[N][20],g[N][20],l[N];
int gcd(int a,int b){
 return b>0?gcd(b,a%b):a;
}
void init(){
 f[n][0]=l[n];g[n][0]=n-l[n];
 for(int i=n-1;i>=2;i--){
 	f[i][0]=min(f[i+1][0],l[i]);
 	g[i][0]=i-f[i][0];
 }
 int tmp=log2(n);
 for(int j=1;j<=tmp;j++){
 	for(int i=(1<<j);i<=n;i++){
 		f[i][j]=f[f[i][j-1]][j-1];
 		g[i][j]=g[i][j-1]+ g[f[i][j-1]][j-1]+(1<<j-1)*(f[i][j-1]-f[i][j]);
 	}
 }
}
int query(int x,int to){//x到区间[to,x-1]内所有点的步数和 
 if(l[x]<=to) return x-to;//第一跳,特判 
 int ans=x-l[x], tot=1;//tot记录已经跳了多少步
 x=l[x];
 for(int i=log2(n);i>=0;i--){
 	if(f[x][i]>=to){
 		ans+= tot*(x-f[x][i])+g[x][i];
 		tot+=(1<<i);x=f[x][i];
 	}
 } 
 if(x>to) ans+= x-to +tot*(x-to);//(?)
 return ans;
}
signed main(){
 cin>>n;
 for(int i=2;i<=n;i++) cin>>l[i];
 init();
 cin>>q;
 int L,R,x;
 int fm,fz,GCD;
 for(int i=1;i<=q;i++){
 	cin>>L>>R>>x;
 	fz=query(x,L)-query(x,R+1);
 	fm=R-L+1;
 	GCD=gcd(fm,fz);
 	fm/=GCD;fz/=GCD;
 	cout<<fz<<"/"<<fm<<endl;
 }
}

单调栈

伪代码

insert x
while !sta.empty() && sta.top()<x
sta.pop()
sta.push(x)

图论

最短路

Dij
const int N=5e4+5;
int n,m,s;
int dis[N],vis[N];
struct edge{
  int u,v,w;
};
vector<edge> e[N];
struct node{
 int id,dis;
 bool operator < (const node &a) const{return dis>a.dis;}
};
signed main(){
 ios::sync_with_stdio(false);
 cin.tie(nullptr);
 cin>>n>>m>>s;
 for(int i=1;i<=m;i++){
    int u,v,w;
    cin>>u>>v>>w;
    e[u].push_back(edge{u,v,w});     
 }
 priority_queue<node> q;
 q.push(node{s,0});
 memset(dis,0x3f,sizeof(dis));
 memset(vis,0,sizeof(vis));
 dis[s]=0;
 while(!q.empty()){
    node a=q.top();q.pop();
    int now=a.id;
    if(vis[now]) continue;
    vis[now]=1;
    for(int i=0;i<e[now].size();i++){
        edge tmp=e[now][i];
        if(dis[tmp.v]>tmp.w+dis[tmp.u]){
            dis[tmp.v]=tmp.w+dis[tmp.u];
            q.push(node{tmp.v,dis[tmp.v]});
        }
    }
 }
 for(int i=1;i<=n;i++)
    cout<<dis[i]<<" ";
}
SPFA
const int N=1e4+5,INF=(1<<31)-1;
int n,m,s,u,v,w;
struct edge{
   int u,v,w;
};
queue<int> q;
vector<edge> g[N];
int vis[N];
int dis[N];
signed main(){
   ios::sync_with_stdio(false);
   cin.tie(0);
   cin>>n>>m>>s;
   for(int i=1;i<=m;i++){
       cin>>u>>v>>w;
       g[u].push_back({u,v,w});
   }
   memset(vis,0,sizeof(vis));
   for(int i=1;i<=n;i++) dis[i]=INF;
   dis[s]=0;
   vis[s]=1;q.push(s);
   while(!q.empty()){
       int now=q.front();q.pop();
       vis[now]=0;
       for(auto nex:g[now]){
           if(dis[nex.v]>dis[nex.u]+nex.w){
               dis[nex.v]=dis[nex.u]+nex.w;
               if(vis[nex.v]==0) q.push(nex.v);
           }
       }
   }
   for(int i=1;i<=n;i++) cout<<dis[i]<<" ";
}
判读负环

负环的定义：一条边权之和为负数的回路。

如果用SPFA判断负环超时了可以想起Var说过的话：

其实大部分题用sqrt(n)能骗过，奇淫技巧（这肯定是错的，但是好多题能过，如果被卡时间的话）
P3385 【模板】负环

题目描述

给定一个 $n$ 个点的有向图，请求出图中是否存在从顶点 $1$ 出发能到达的负环。负环的定义是：一条边权之和为负数的回路。

输入格式

本题单测试点有多组测试数据。

输入的第一行是一个整数 $T$ ，表示测试数据的组数。对于每组数据的格式如下：第一行有两个整数，分别表示图的点数 $n$ 和接下来给出边信息的条数 $m$ 。接下来 $m$ 行，每行三个整数 $u, v, w$ 。

若 $w \geq 0$ ，则表示存在一条从 $u$ 至 $v$ 边权为 $w$ 的边，还存在一条从 $v$ 至 $u$ 边权为 $w$ 的边。

若 $w < 0$ ，则只表示存在一条从 $u$ 至 $v$ 边权为 $w$ 的边。

输出格式

对于每组数据，输出一行一个字符串，若所求负环存在，则输出 YES，否则输出 NO。

输入 #1
2
3 4
1 2 2
1 3 4
2 3 1
3 1 -3
3 3
1 2 3
2 3 4
3 1 -8
输出 #1
NO
YES
说明/提示

数据规模与约定

对于全部的测试点，保证：

$1 \leq n \leq 2 \times 10^3$ ， $1 \leq m \leq 3 \times 10^3$ 。

$1 \leq u, v \leq n$ ， $-10^4 \leq w \leq 10^4$ 。

$1 \leq T \leq 10$ 。

提示

请注意， $m$ 不是图的边数。

注意本题只是找从1出发能到达的负环。

如果是全图判负环应该是开始时把所有点入队。
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=2e3+5;
int n,m,u,v,w,t;
struct edge{
 int u,v,w;
};
vector<edge> g[N];
int vis[N],dis[N],cnt[N];
void spfa(){
 queue<int> q;
 vis[1]=1;q.push(1);dis[1]=0;
 while(!q.empty()){
 	int now=q.front();q.pop();
 	vis[now]=0;
 	for(auto nex:g[now]){
 		if(dis[nex.v]>dis[nex.u]+nex.w){
 			dis[nex.v]=dis[nex.u]+nex.w;
 			if(vis[nex.v]==0){
 				vis[nex.v]=1;
 				cnt[nex.v]=cnt[nex.u]+1;   
 				q.push(nex.v);
 				if(cnt[nex.v]>=n){cout<<"YES"<<endl;return;}
 			}
 		}
 	}
 }
 cout<<"NO"<<endl;
}
signed main(){
 ios::sync_with_stdio(false);
 cin.tie(0);
 cin>>t;
 while(t--){
 	memset(vis,0,sizeof(vis));
 	memset(dis,0x3f,sizeof(dis));
 	memset(cnt,0,sizeof(cnt));
 	cin>>n>>m;
 	for(int i=1;i<=m;i++){
 		cin>>u>>v>>w;
 		if(w<0) g[u].push_back({u,v,w});
 		else{
 			g[u].push_back({u,v,w});
 			g[v].push_back({v,u,w});
 		}
 	}
 	spfa(); 
 	for(int i=1;i<=n;i++) g[i].clear();
 }
}	
二维最短路模板

次短路

P2865 [USACO06NOV] Roadblocks G

题目描述

贝茜把家搬到了一个小农场，但她常常回到 FJ 的农场去拜访她的朋友。贝茜很喜欢路边的风景，不想那么快地结束她的旅途，于是她每次回农场，都会选择第二短的路径，而不象我们所习惯的那样，选择最短路。贝茜所在的乡村有 R(1≤R≤105) 条双向道路，每条路都联结了所有的 N(1≤N≤5000) 个农场中的某两个。贝茜居住在农场 1，她的朋友们居住在农场 N（即贝茜每次旅行的目的地）。贝茜选择的第二短的路径中，可以包含任何一条在最短路中出现的道路，并且，一条路可以重复走多次。当然咯，第二短路的长度必须严格大于最短路（可能有多条）的长度，但它的长度必须不大于所有除最短路外的路径的长度。

输入格式

Line 1: Two space-separated integers: N and R

Lines 2:R+1: Each line contains three space-separated integers: A, B, and D that describe a road that connects intersections A and B and has length D (1 ≤ D ≤ 5000)

输出格式

Line 1: The length of the second shortest path between node 1 and node N0

输入 #1
4 4
1 2 100
2 4 200
2 3 250
3 4 100
输出 #1
450
说明/提示

Two routes: 1 -> 2 -> 4 (length 100+200=300) and 1 -> 2 -> 3 -> 4 (length 100+250+100=450)

法1思路：

从1做一次最短路存在dis1[]中，从n做一次最短路存在dis2[]中，从1到n的最短路长度为dis1[n](或者dis2[1]) 然后遍历每一条边(u,v,w): if(dis1[u]+w+dis2[v]>dis1[n]) ans=min(ans,dis1[u]+w+dis2[v])
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=1e5+5;
const int INF=0x3f3f3f3f3f3f3f3f;
int r,n,u,v,w;
int dis1[N],vis[N],dis2[N];
struct edge{
int u,v,w;
};
struct node{
int val,id;
bool operator <(const node &x)const{return val>x.val;}
};
vector<edge> e[N];
priority_queue<node> q;
signed main(){
   ios::sync_with_stdio(false);
   cin.tie(nullptr);
   cin>>n>>r;
   for(int i=1;i<=r;i++){
       cin>>u>>v>>w;
       e[u].push_back({u,v,w});
       e[v].push_back({v,u,w});
   }
   memset(dis1,0x3f,sizeof(dis1));
   q.push({0,1});dis1[1]=0;
   while(!q.empty()){
       node now=q.top();q.pop();
       u=now.id;
       if(vis[u]) continue;
       vis[u]=1;
       for(auto edg:e[u]){
           v=edg.v,w=edg.w;
           if(dis1[u]+w<dis1[v]){
               dis1[v]=dis1[u]+w;
               q.push({dis1[v],v});
           }
       }
   }
   memset(dis2,0x3f,sizeof(dis2));
   q.push({0,n});dis2[n]=0;
   memset(vis,0,sizeof(vis));
   while(!q.empty()){
       node now=q.top();q.pop();
       u=now.id;
       if(vis[u]) continue;
       vis[u]=1;
       for(auto edg:e[u]){
           v=edg.v,w=edg.w;
           if(dis2[u]+w<dis2[v]){
               dis2[v]=dis2[u]+w;
               q.push({dis2[v],v});
           }
       }
   }
   int ans=INF;
   for(int u=1;u<=n;u++)
   for(auto edg:e[u]){
       v=edg.v,w=edg.w;
       if(dis1[u]+w+dis2[v]>dis1[n]) 
       	ans=min(ans,dis1[u]+w+dis2[v]);
   }
   cout<<ans;
}

最长路

SPFA

const int N=2e3+5,INF=(1<<31)-1;
int n,m,s,u,v,w;
struct edge{
 int u,v,w;
};
queue<int> q;
vector<edge> g[N];
int vis[N];
int dis[N];
signed main(){
 ios::sync_with_stdio(false);
 cin.tie(0);
 cin>>n>>m;
 for(int i=1;i<=m;i++){
     cin>>u>>v>>w;
     g[u].push_back({u,v,-w});
 }
 memset(vis,0,sizeof(vis));
 for(int i=1;i<=n;i++) dis[i]=INF;
 dis[1]=0;
 vis[1]=1;q.push(1);
 while(!q.empty()){
     int now=q.front();q.pop();
     vis[now]=0;
     for(auto nex:g[now]){
         if(dis[nex.v]>dis[nex.u]+nex.w){
             dis[nex.v]=dis[nex.u]+nex.w;
             if(vis[nex.v]==0) q.push(nex.v);
         }
     }
 }
 if(dis[n]==INF) cout<<-1<<endl;
 else cout<<-dis[n]<<endl;
}

最小生成树(MST)

Kruskal

按照边权升序排序（直接建边的数组）；遍历每一条边，只要两个端点不属于一个并查集就选上；如果选了n-1条边则保证最小生成树存在。

const int N=5e3+5;
const int M=2e5+5;
int n,m;
int s[N];
struct edge{
int u,v,w;
}edg[M];
bool cmp(edge x,edge y){return x.w<y.w;}
int find(int x){return s[x]==x?x:s[x]=find(s[x]);}
void merge(int x,int y){
	x=find(x);y=find(y);
	if(x!=y) s[x]=s[y];
}
bool jud(int x,int y){return find(x)==find(y);}
signed main(){
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cin>>n>>m;
    for(int i=1;i<=n;i++) s[i]=i;
    for(int i=1;i<=m;i++)
    cin>>edg[i].u>>edg[i].v>>edg[i].w;
    int cnt=0,sum=0;
    sort(edg+1,edg+m+1,cmp);
    for(int i=1;i<=m;i++){
    edge tmp=edg[i];
    if(!jud(tmp.u,tmp.v)){
        cnt++;
        sum+=tmp.w;
        merge(tmp.u,tmp.v);
    }
    if(cnt==n-1) break;
    }
    if(cnt<n-1) cout<<"orz";
    else cout<<sum;
    return 0;
}

Tarjan缩点(单连通分量)

P3387 【模板】缩点

给定一个 $n$ 个点 $m$ 条边有向图，每个点有一个权值，求一条路径，使路径经过的点权值之和最大。你只需要求出这个权值和。允许多次经过一条边或者一个点，但是，重复经过的点，权值只计算一次。

第一行两个正整数 $n,m$ 。第二行 $n$ 个整数，其中第 $i$ 个数 $a_i$ 表示点 $i$ 的点权。第三至 $m+2$ 行，每行两个整数 $u,v$ ，表示一条 $u\rightarrow v$ 的有向边。

$1\le n \le 10^4$ ， $1\le m \le 10^5$ ， $0\le a_i\le 10^3$ 。

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define INF 0x3f3f3f3f3f3f3f3f
#define fi first
#define se second
const int mod=1e9+7;
const double PI=acos(-1);
const int N=1e5+5;
int w[N],ww[N];//w[]-原图点权 w1[]-缩点后的点权
int dfn[N],low[N],dfsid;//dfn[]-DFS时间戳 low[]-可到达的最小时间戳
int grp[N],grpid;//grp[i]-i属于哪个SCC
vector<int> st;//实现栈
vector<int> e[N],ee[N];
unordered_set<int> vis;
int pair_hash(int u,int v){return u*N+v;}
void tarjan(int u){
    dfn[u]=low[u]=++dfsid;
    st.push_back(u);
    for(int v:e[u]){
        if(!dfn[v]){
            tarjan(v);
            low[u]=min(low[u],low[v]);
        }else if(!grp[v]){
            low[u]=min(low[u],dfn[v]);
        }
    }
    if(dfn[u]==low[u]){
        grp[u]=++grpid;
        ww[grpid]=w[u];
        while(st.back()!=u){
            grp[st.back()]=grpid;
            ww[grpid]+=w[st.back()];
            st.pop_back();
        }
        st.pop_back();
    }
}
int dp[N];
int dfs(int u){
    if(dp[u]!=-1) return dp[u];
    int tmp=0;
    for(int v:ee[u]) tmp=max(tmp,dfs(v));
    return dp[u]=tmp+ww[u];
}
int n,m,u,v,uu,vv,ans;
signed main(){
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>w[i];
    for(int i=1;i<=m;i++){
        cin>>u>>v;
        e[u].push_back(v);
    }
    for(int i=1;i<=n;i++) if(!dfn[i]) tarjan(i);
    for(int u=1;u<=n;u++){
        for(auto v:e[u]){
            uu=grp[u],vv=grp[v];
            if(uu!=vv&&vis.count(pair_hash(uu,vv))==0){
                vis.insert(pair_hash(uu,vv));
                ee[uu].push_back(vv);
            }
        }
    }
    memset(dp,-1,sizeof(dp));
    for(int i=1;i<=n;i++) ans=max(ans,dfs(i));
    cout<<ans;
    return 0;
}

LCA

1.Tarjan

const int N=5e5+5;
int n,m,u,v,root;
vector<int> e[N];
vector<pair<int,int>> query[N];
int fa[N],vis[N],ans[N];
int find(int u){
    if(u==fa[u]) return u;
    else return fa[u]=find(fa[u]);
}
void tarjan(int u){
    vis[u]=1;
    for(int v:e[u]){
        if(!vis[v]){
            tarjan(v);
            fa[v]=u;
        }
    }
    for(auto q:query[u]){
        int v=q.first,i=q.second;
        if(vis[v]) ans[i]=find(v);
    }
}
signed main(){
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cin>>n>>m>>root;
    for(int i=1;i<n;i++){
        cin>>u>>v;
        e[u].push_back(v);
        e[v].push_back(u); 
    }
    for(int i=1;i<=m;i++){
        cin>>u>>v;
        query[u].push_back({v,i});
        query[v].push_back({u,i});
    }
    for(int i=1;i<N;i++) fa[i]=i;
    tarjan(root);
    for(int i=1;i<=m;i++) cout<<ans[i]<<endl;
    return 0;
}

2.倍增算法

#include<bits/stdc++.h>
using namespace std;
const int N=5e5+5;
const int M=19;
int n,m,s,a,b;
vector<int> e[N];
int dep[N],fa[N][20];
void dfs(int u,int father){
	dep[u]=dep[father]+1;
	fa[u][0]=father;
	for(int i=1;i<=M;i++)
		fa[u][i]=fa[fa[u][i-1]][i-1];
	for(int v:e[u])
		if(v!=father) dfs(v,u);
}
int lca(int u,int v){
	if(dep[u]<dep[v]) swap(u,v);
	//先跳到同一层 
	for(int i=M;i>=0;i--)
		if(dep[fa[u][i]]>=dep[v])
			u=fa[u][i];
	if(u==v) return v;
	for(int i=M;i>=0;i--)
		if(fa[u][i]!=fa[v][i])
			u=fa[u][i],v=fa[v][i];
	return fa[u][0];
}
signed main(){
	cin>>n>>m>>s;
	for(int i=1;i<n;i++){
		cin>>a>>b;
		e[a].push_back(b);
		e[b].push_back(a);
	}
	dfs(s,0);
	for(int i=1;i<=m;i++){
		cin>>a>>b;
		cout<<lca(a,b)<<endl;
	}
}

拓扑排序

拓扑排序无解判断（可以用来判环）如果队列已空，但还有点未入队（ans.size()<n)

BFS模板

queue<int> q;
vector<int> G[N];
vector<int> ans; //存放拓扑序列
int in[N];
bool bfs_topsort(int n){ //n为节点个数
	for(int i=1;i<=n;i++) 
   		if(in[i]==0) q.push(i);  //将入度为0的点入队列
	while(!q.empty()){
		int u=q.front();q.pop(); //选一个入度为 0 的点，出队
		ans.push_back(u);
		for(int i=0;i<G[u].size();i++){
			int v=G[u][i];
			if(--in[v]==0) q.push(v); //当某一条边的入度为0，入队
		}
	}
	if(ans.size()==n){
		for(int i=0;i<ans.size();i++)
			printf("%d%c",ans[i],i==ans.size()-1?'\n':' ');
		return true;
	}
	return false;
}

二叉树的三种遍历方式

用一维数组模拟树(适合层序输出）

    1
  2    3
4  5  6  7
8 
void init(int n){
	for(int i=1;i<=n;i++){
		if((i<<1)<=n) node[i].l=i<<1;
		if((i<<1|1)<=n) node[i].r=i<<1|1;
	}
}

后序遍历（输出）：左->右->根

后序：8->4->5->2->6->7->3->1
void Post(int x){
	if(node[x].l!=0) Post(node[x].l);//访问左节点
	if(node[x].r!=0) Post(node[x].r);//访问右节点
	cout<<node[x].val;//访问根节点
}

中序遍历（输出）：左->根->右

中序：8->4->2->5->1->6->3->7
void In(int x){
	if(node[x].l!=0) In(node[x].l);
	cout<<node[x].val;
	if(node[x].r!=0) In(node[x].r);
}

先序遍历（输出）：根->左->右

先序：1->2->4->8->5->3->6->7
void Pre(int x){
	cout<<node[x].val;
	if(node[x].l!=0) Pre(node[x].l);
	if(node[x].r!=0) Pre(node[x].r);
}

其他

map对key降序排列

map<int,int,greater<int>> mp;

二分答案

int l=1,r=n,mid,ans;
while(l<=r){
	mid=l+r>>1;	
    if(a[mid]>=tmp) r=mid-1;
	else l=mid+1;
}

第k小的数（经典双指针对搜+二分答案）

f(x)表示多少对i,j满足a[i]+b[j]<=x.
f(x)<=f(x+1),单调
只需找最小的x使得f(x)>=k.

关键：对于给定的x，如何统计有多少对i,j满足a[i]+b[j]<=x(重复的最后一个) a[1...n],b[1...m]数组排序后双指针（一个从前一个从后搜，使得实现线性复杂度） int f(int x){ int cnt=0; int j=m; for(int i=1;i<=n;i++){ while(j&&a[i]+b[j]>x) j--; cnt+=j; } return cnt; }
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+5;
int a[N],b[N];
int n,m,k,l,r,mid;
int f(int x){
  int cnt=0;
  int j=m;
  for(int i=1;i<=n;i++){
  	while(a[i]+b[j]>=x) j--;
  	cnt+=j;
  }
  return cnt;
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
int t;cin>>t;
while(t--){
  	cin>>n>>m>>k;
  	for(int i=1;i<=n;i++) cin>>a[i];
  	for(int j=1;j<=m;j++) cin>>b[j];
  	sort(a+1,a+n+1);
  	sort(b+1,b+m+1);
  	l=a[1]+b[1],r=a[n]+b[m];
  	while(l<=r){
  		mid=(l+r)>>1;
  		int tmp=f(mid);
  		if(tmp<k) l=mid+1;
  		else r=mid-1;
  	}
  	cout<<r<<endl;
  }
}

随机数种子

using ull=unsigned long long;
mt19937_64 rg(random_device{}());

春联10.1009（最长区间乘积为平方数）

图片上传失败，请重新上传

法1：（随机映射 + 前缀异或）

#include<bits/stdc++.h>
using namespace std;
#define INF 0x3f3f3f3f3f3f3f3f
#define rep(i,j,k) for (int i=j;i<=k;++i)
#define per(i,j,k) for (int i=j;i>=k;--i)
#define fi first
#define se second
#define int long long
#define endl '\n'
const int M=1e6+5;
const int N=1e5+5;
using ull=unsigned long long;
mt19937_64 rg(random_device{}());
int n,m;
bitset<M> vis;
ull v[M];
pair<ull,int> a[N];
void solve(){
  cin>>n;
  int tmp,qzj=0;
  a[0]={0,0};
  rep(i,1,n){
  	cin>>tmp,qzj^=v[tmp];
  	a[i]={qzj,i};
  }
  sort(a,a+n+1);
  int ans_l=-2,ans_r=-1,l,r;
  for(l=0;l<=n;l=r+1){
  	for(r=l;r<n&&a[r+1].fi==a[l].fi;r++);
  	int p=a[l].se,q=a[r].se;
  	if(q-p>ans_r-ans_l) ans_l=p,ans_r=q;
  	else if(q-p==ans_r-ans_l&&(p<ans_l||ans_l<0)) ans_l=p,ans_r=q;
  }
  cout<<ans_l+1<<" "<<ans_r<<endl;
}
signed main(){
  ios::sync_with_stdio(false);
  cin.tie(nullptr);
  for(int i=2;i<M;i++)
  	if(!vis[i]){
  		v[i]=rg();
  		for(int j=i+i;j<M;j+=i){
  			v[j]=v[j/i]^v[i];
  			vis[j]=1;//标记合数
  		}
  	}
  int t;cin>>t;
  while(t--) solve();
  return 0;
}

预处理：O (M log log M)，其中 M 为筛法上限（1e6）。
单次查询：O (N log N)，主要来自排序操作。
总复杂度：O (M log log M + T・N log N)，适用于多组数据。

字符串

manacher

char s[N<<1];//修改串
int d[N<<1];//回文半径函数
int getstr(string str){//返回修改串后的长度
   int k=0;
   s[0]='@',s[++k]='#';
   for(auto u:str){
	   s[++k]=u;
	   s[++k]='#';
   }
   s[k+1]='$';
   return k;
}
void manacher(int n){
   d[1]=1;
   for(int i=2,l=1,r=1;i<=n;i++){
	   if(i<=r) d[i]=min(d[r-i+l],r-i+1);
	   while(s[i-d[i]]==s[i+d[i]]) d[i]++;
	   if(i+d[i]-1>r) l=i-d[i]+1,r=i+d[i]-1;
   }
}

manacher题目

1.统计回文串个数

const int N=1e5+5;
int n,a[N],delt[N];
int s[N<<1];//修改串
int d[N<<1];//回文半径函数
int getstr(){//返回修改串后的长度
   int k=0;
   s[0]=1832539553,s[++k]=-INF;
   rep(i,1,n){
      s[++k]=delt[i];
      s[++k]=-INF;
   }
   s[k+1]=18858876509;
   return k;
}
void manacher(int n){
   //d[i]为回文半径,以i为中心的回文串长度为(d[i]-1)
   rep(i,1,n) d[i]=0;
   d[1]=1;
   for(int i=2,l=1,r=1;i<=n;i++){
      if(i<=r) d[i]=min(d[l+(r-i)],r-i+1);
      while(s[i-d[i]]==s[i+d[i]]) d[i]++;
      if(i+d[i]-1>r) l=i-d[i]+1,r=i+d[i]-1;
   }
}
void solve(){
   cin>>n;
   int ans=n;
   rep(i,1,n) cin>>a[i];
   rep(i,2,n) delt[i-1]=a[i]-a[i-1];
   n-=1;
   int len=getstr();
   manacher(len);
   rep(i,1,len)
      ans+=d[i]/2;
   cout<<ans<<endl;
}
signed main(){
   ios::sync_with_stdio(false);
   cin.tie(nullptr);
   int t;cin>>t;
   while(t--) solve();
   return 0;
}
/*1 3 5 2 4
# 2 # 2 # -3 # 2 #
1 2 2 2 1  4 1 2 1 
0 1 1 1 0  2 0 1 0 
*/

2.最长双回文子串(一个子串可以分为两个回文串)

const int N=1e5+5;
char s[N<<1];//修改串
int d[N<<1];//回文半径函数
int getstr(string str){//返回修改串后的长度
   int k=0;
   s[0]='@',s[++k]='#';
   for(auto u:str){
     s[++k]=u;
     s[++k]='#';
   }
   s[k+1]='$';
   return k;
}
void manacher(int n){
   d[1]=1;
   for(int i=2,l=1,r=1;i<=n;i++){
     if(i<=r) d[i]=min(d[r-i+l],r-i+1);
     while(s[i-d[i]]==s[i+d[i]]) d[i]++;
     if(i+d[i]-1>r) l=i-d[i]+1,r=i+d[i]-1;
   }
}
int pre[N<<1],suf[N<<1];
signed main(){
   ios::sync_with_stdio(false);
   cin.tie(nullptr);
   string ss;
   cin>>ss;
   int len=getstr(ss);
   manacher(len);
   rep(i,2,len) pre[i+d[i]-1]=max(pre[i+d[i]-1],d[i]-1);
   for(int i=len;i>=3;i-=2) pre[i-2]=max(pre[i-2],pre[i]-2);
   per(i,len-1,1) suf[i-d[i]+1]=max(suf[i-d[i]+1],d[i]-1);
   for(int i=1;i<=len-4;i+=2) suf[i+2]=max(suf[i+2],suf[i]-2);
   int ans=0;
   for(int i=3;i<=len-2;i+=2)
      ans=max(ans,pre[i]+suf[i]);
   cout<<ans;
   return 0;
}

3.前k长回文子串长度乘积

const int mod=19930726;
const int N=1e6+5;
int n,k;
int ksm(int a,int b,int c){
   int ans=1;
   while(b){
     if(b&1) ans=(ans*a)%c;
     b>>=1;
     a=(a*a)%c;
   }
   return ans;
}
string s;
int d[N];//回文半径函数
void manacher(int n){
   d[1]=1;
   for(int i=2,l=1,r=1;i<=n;i++){
     if(i<=r) d[i]=min(d[r-i+l],r-i+1);
     while(s[i-d[i]]==s[i+d[i]]) d[i]++;
     if(i+d[i]-1>r) l=i-d[i]+1,r=i+d[i]-1;
   }
}
int cnt[N];
   signed main(){
   ios::sync_with_stdio(false);
   cin.tie(nullptr);
   cin>>n>>k;
   cin>>s;
   s=" "+s;
   int sum=0;
   int ans=1;
   manacher(n);
   int up=0;
   rep(i,1,n){
      cnt[d[i]*2-1]++;
      up=max(up,d[i]*2-1);
   }
   for(int i=up;i>=1;i-=2){
      sum+=cnt[i];
      if(sum>=k){
          ans=ans*ksm(i,k,mod)%mod;
          k-=sum;
          break;
      }else{
          ans=ans*ksm(i,sum,mod)%mod;
          k-=sum;
      }
   }
   if(k>0) cout<<-1;
   else cout<<ans;
   return 0;
}

kmp

int nxt[N];//模式串P[1,i]中最长相等前后缀的长度
int ls,lp;//ls:S的长度,lp:P的长度
string S,P;
void kmp(){
	cin>>S>>P;
	ls=S.size(),lp=P.size();
	S=" "+S,P=" "+P;
	nxt[1]=0;
	for(int i=2,j=0;i<=lp;i++){
		while(j&&P[i]!=P[j+1]) j=nxt[j];
		if(P[i]==P[j+1]) j++;
		nxt[i]=j;
	}
	for(int i=1,j=0;i<=ls;i++){
		while(j&&S[i]!=P[j+1]) j=nxt[j];
		if(S[i]==P[j+1]) j++;
		if(j==lp) cout<<i-lp+1<<endl;
		//按从小到大的顺序输出P在S中出现的位置
	}
	for(int i=1;i<=lp;i++) cout<<nxt[i]<<" ";
}

1.最短循环节问题

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5;
string s;
int nxt[N];
signed main(){
   ios::sync_with_stdio(false);
   cin.tie(0);
   int ls;
   cin>>ls;
   cin>>s;
   s=" "+s;
   nxt[1]=0;
   for(int i=2,j=0;i<=ls;i++){
   while(j&&s[i]!=s[j+1]) j=nxt[j];
   if(s[i]==s[j+1]) j++;
   nxt[i]=j;
   }
   cout<<ls-nxt[ls];
}    #include<bits/stdc++.h>
using namespace std;
const int N=1e6+5;
string s;
int nxt[N];
signed main(){
   ios::sync_with_stdio(false);
   cin.tie(0);
   int ls;
   cin>>ls;
   cin>>s;
   s=" "+s;
   nxt[1]=0;
   for(int i=2,j=0;i<=ls;i++){
   while(j&&s[i]!=s[j+1]) j=nxt[j];
   if(s[i]==s[j+1]) j++;
   nxt[i]=j;
   }
   cout<<ls-nxt[ls];
}

2.在S中不断删除P

const int N=1e6+5;
int nxt[N];//模式串P[1,i]中最长相等前后缀的长度
int ls,lp;//ls:S的长度,lp:P的长度
int st[N],top=0;//栈，维护删除后的答案
int f[N];//f[i]:i能匹配到的最大p[j]位置的j
string S,P;
void kmp(){
   cin>>S>>P;
   ls=S.size(),lp=P.size();
   S=" "+S,P=" "+P;
   nxt[1]=0;
   for(int i=2,j=0;i<=lp;i++){
       while(j&&P[i]!=P[j+1]) j=nxt[j];
       if(P[i]==P[j+1]) j++;
       nxt[i]=j;
   }
   for(int i=1,j=0;i<=ls;i++){
       while(j&&S[i]!=P[j+1]) j=nxt[j];
       if(S[i]==P[j+1]) j++;
       f[i]=j;//记录i对应的j值
       st[++top]=i;//入栈
       if(j==lp){//匹配成功
           top-=lp;//栈里弹出元素
           j=f[st[top]];//更新j值
       }
   }
   for(int i=1;i<=top;i++) cout<<S[st[i]];
}
signed main(){
   ios::sync_with_stdio(false);
   cin.tie(nullptr);
   kmp();
   return 0;
}

to_string和stoi函数

头文件都是#include<string>

to_string函数

功能：将数字常量（int,double,long等）转换成字符串（string）。

1.支持带负号

2.若对double类型进行操作默认保留六位小数。
cout<<to-string(-123)[0];
<< -
---
cout<<to_string(123.456);
<< 123.456000
stoi函数

功能：将n（默认为10）进制的字符串转换成十进制数字常量。

1.支持正负号

2.支持定义原本字符串为几进制数字字符串。
string a="-12";
cout<<stoi(a)<<endl;
<<-12
cout<<stoi(a,0,16)<<endl;
<<-18
(手写)字符串正整数转int
int tran(string x){
  int tmp=0;
  for(int i=x.length()-1;i>=0;i--){
  	tmp*=10;
  	tmp+=x[i]-'0';
  }
  return tmp;
}

去重函数unique()

去除容器或者数组中相邻元素之间重复出现的元素

unique三个参数:

1.数据集起始地址

2.数据集最后一个元素的下一个地址

3.比较函数(一般省略)

返回值:去重后的不重复数组中最后一个元素的下一个元素的地址(是类似于0x的真正地址)

搭配sort实现整体数组去重(O(n+nlogn))

1.vector容器
sort(a.begin(),a.end());
int cnt=unique(a.begin(),a.end())-a.begin();
2.数组
sort(a+1,a+n+1);
//同时实现'去重'和'求去重后的元素个数'
int cnt=unique(a+1,a+n+1)-(a+1);
//cnt为去重后的数量

进制哈希BKDHash

统计不同字符串的个数

#include <bits/stdc++.h>
#define ull unsigned long long
using namespace std;
const int N=1e4+5;
ull a[N];//ull隐式取模2^64 
string s;
ull BKDRHash(string s){
	ull p=131,res=0;
	for(int i=0;i<s.length();i++)
		res=res*p+s[i];
	return res;
}
signed main(){
int n;cin>>n;
for(int i=1;i<=n;i++){
		cin>>s;
		a[i]=BKDRHash(s);
	}
	int ans=0;
	sort(a+1,a+n+1);
	//ans=unique(a+1,a+n+1)-(a+1);去重函数，与下面循环等价
	for(int i=1;i<=n;i++)
		if(a[i]!=a[i+1]) ans++;
	cout<<ans;
}

字符串匹配数组

问题大意：原来为子串的字符串需要增加多少个字符来使得变成不是其子串。

思路：预处理一个匹配数组，每次询问的时候匹配即可。(倒着遍历来处理跳跃查找的操作）

实现：

nxt_id[i][j]:a[i]字符之后的第一个字符j(0<=j<26)的出现位置

dp[i]:若前i个字符与字符串完全匹配，则还需要增加几个字符

lst[i]:字符i上一次出现的位置

预处理：
memset(dp,0x3f,sizeof(dp));
dp[n+1]=0;
for(int j=0;j<k;j++) nxt_id[n+1][j]=lst[j]=n+1;
for(int i=n;i>=0;i--){
  for(int j=0;j<k;j++){
  	nxt_id[i][j]=lst[j];
  	dp[i]=min(dp[i],dp[nxt_id[i][j]]+1);
  }
  if(i!=0) lst[a[i]-'a']=i;
}
查询：
int q;cin>>q;
while(q--){
  string s;
  cin>>s;
  int id=0;
  for(int i=0;i<s.size();i++)
  	id=nxt_id[id][s[i]-'a'];
  cout<<dp[id]<<endl;
}

25校赛模板

我的头

数学

数论

欧拉线性筛

质因数分解

GCD，LCM

线性逆元

扩展欧几里得

中国剩余定理（Chinese Remainder Theorem）

扩展中国剩余定理（Extended Chinese Remainder Theorem）

欧拉函数

·1.求正整数n的欧拉函数φ(n)

·2.欧拉函数的线性求法

扩展欧拉函数/欧拉降幂(ex_eular)

求a**b(mod c)

组合数学

线性逆元，组合数

Lacus定理

其他

快速幂

lowbit

求二进制数中1的个数

复数

FFT

二维坐标映射

矩阵，矩阵快速幂

高斯消元

P2455 [SDOI2006] 线性方程组

题目描述

输入格式

输出格式

输入 #1

输出 #1

容斥原理

拉格朗日插值公式

动态规划

四边形不等式优化

数位DP

P87654

数列计数(春联3.1001)

数据结构

堆（题目）

P1168 中位数

通过维护一个大根堆、一个小根堆的保持可以直接查询到中位数。

对于2i+1个数，大根堆存排序后前i个数，小根堆存排序后后i+1个数。

线段树1

线段树2

(线段树)区间最大子段和 [P4513 小白逛公园]

P4513 小白逛公园

输入格式

输出格式

输入 #1

输出 #1

并查集

并查集判断连通块个数

P1197 [JSOI2008] 星球大战

带权值并查集+二分图

P1525 [NOIP 2010 提高组] 关押罪犯

P1525 [NOIP 2010 提高组] 关押罪犯

题目背景

题目描述

输入格式

输出格式

输入输出样例 #1

输入 #1

输出 #1

说明/提示

题解：

那么，再结合**敌人的敌人和自己在一个监狱的规律合并 ( 二分图思想 )**。

种类并查集/扩展域并查集

引入

利用并查集本身‘连通性’表示’关系’，用‘坐标区间’表示‘属性’。

P1892 [BalticOI 2003] 团伙

Q:为什么是朋友的情况下不加上merge(x+n,y+n);

Ans(Devin):那句话翻译过来就是“两个朋友各自的敌人是不是需要变成朋友”。

把拓展域并查集理解成’虚拟节点‘：a的敌人a+n，但不知道具体是谁，但是后面把敌人都放到这个并查集里。

P2024 [NOI2001] 食物链

P2024 [NOI2001] 食物链

题目描述

那么，再结合敌人的敌人和自己在一个监狱的规律合并 ( 二分图思想 )。