题目描述

我们输入一个n, 代表我们有n个火车, 接下来我们输入n个数字, 代表了我们的火车的入站的顺序, 然后给问我们有多少种出站的顺序, 要求从字典序小到大输出

题解

解法一: 全排列

实现思路

我们可以知道这么一个问题, 我们的全排列函数是从字典序从小到大的, 然后我们直接调用这个函数就可以了, 每次我们去检测一下我们当前的这个序列是否可以根我们一开始的入站顺序所构成, 如果可以构成, 那么我们这个就是成立的, 否则就是不成立的

图解代码

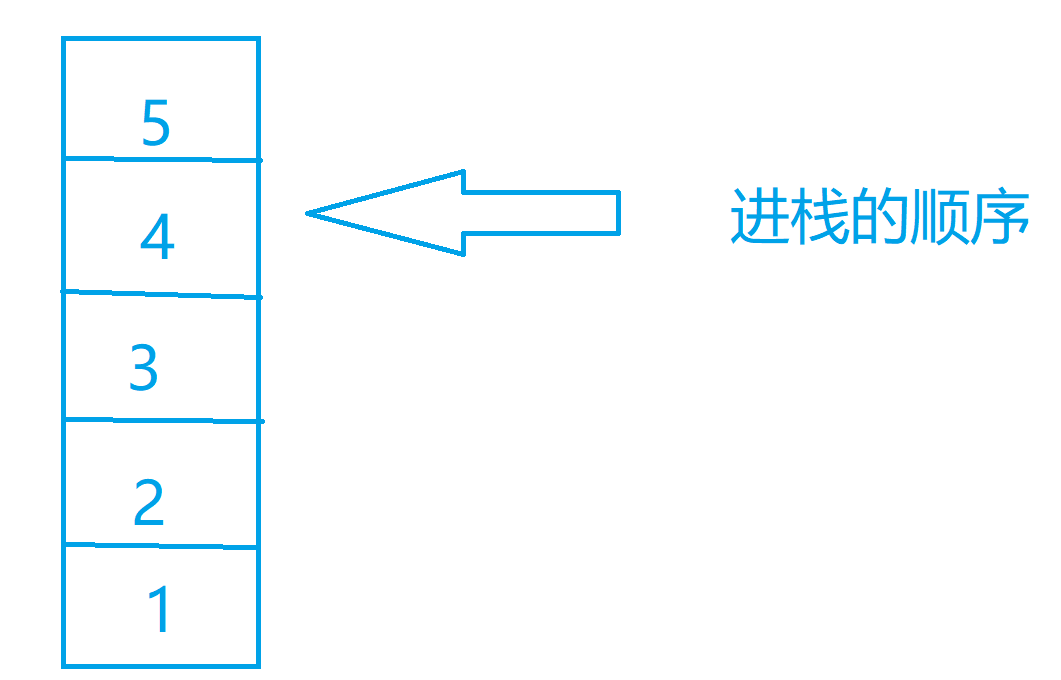
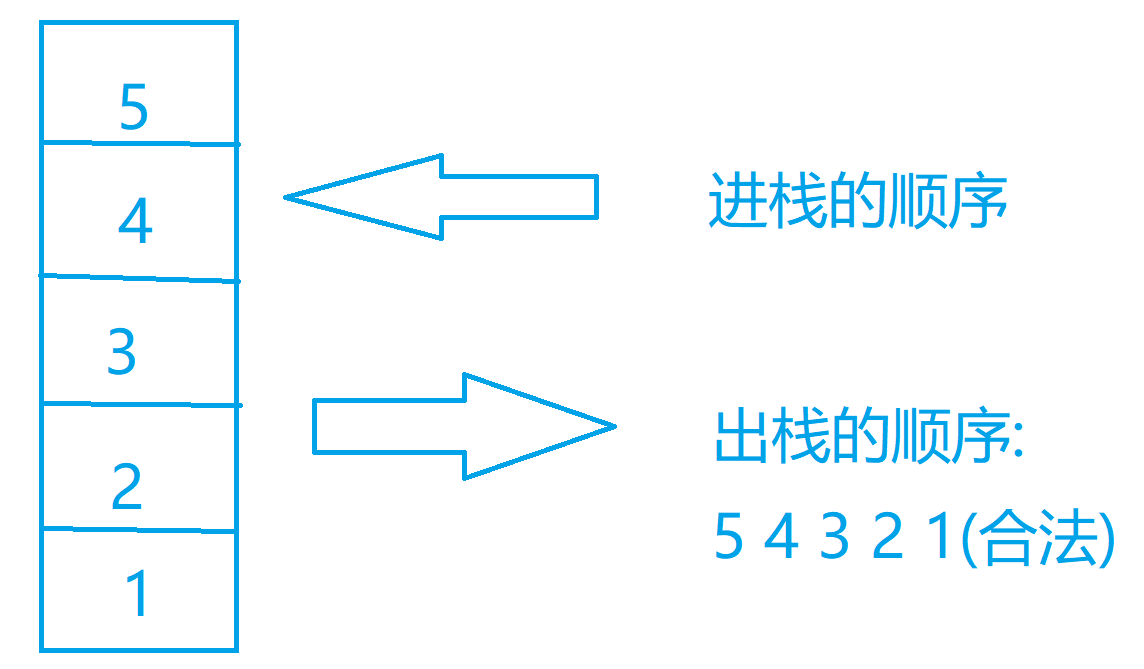
代码实现

#include <bits/stdc++.h>

using namespace std;

bool check(vector<int> &a, vector<int> &cmp) {
    stack<int> st;
    int j = 0, i = 0;
    for (i = 0; i < a.size(); i++) {
        // 依次把我们的a数组中的数入栈
        st.push(a[i]);
        while (j < a.size() && st.size() != 0 && cmp[j] == st.top()) {
            // 依次判断每cmp每个序列的值是否与栈顶相等
            st.pop();
            j++;
        }
    }
    return st.empty();
    // 判断是否可以一一对应上, 可以的话, 就是我们最后的答案
}

signed main() {
    int n;
    cin >> n;
    vector<int> a(n);
    for (auto &it : a) cin >> it;
    vector<int> cmp = a;
    // 我们输入我们的这个数组, 然后我们开一个临时数组
    sort(cmp.begin(), cmp.end());
    // 这个我们先排序
    do {
        if (check(a, cmp)) {
            for (int i = 0; i < n; i++) cout << cmp[i] << " \n"[i == n - 1];
        }
        // 如果可以满足条件, 我们就直接输出
    } while (next_permutation(cmp.begin(), cmp.end()));
    return 0;
}

时空复杂度分析

时间复杂度: $O(n\ast n!)O(n\; *\; n!)$

理由如下: 我们的全排列的函数他的时间复杂度是$n!n!$, 然后我们每次判断的时间复杂度是$nn$的, 所以我们的时间复杂度就是两部分之积

空间复杂度: $O(n)O(n)$

理由如下: 事实上我们只是简单的开辟了两个长度为n的数组, 还有一个存储的栈结构, 所以我们的空间复杂度是$O(n)O(n)$的

解法二: DFS

实现思路

我们其实可以发现, 我们其实每次就是两个操作, 一个是入栈, 一个出栈, 然后因为我们解法一的本质其实就是全排列问题, 我们这里的全排列用dfs实现就可以了, 详细过程在代码的注释里面

代码实现

#include <bits/stdc++.h>

using namespace std;

signed main() {
    int n;
    cin >> n;
    vector<int> a(n);
    for (auto &it : a) cin >> it;
    stack<int> st;
    // 在我们栈里面的车
    vector<int> tmp;
    // 这个是我们出栈的车是什么
    set<vector<int>> res;
    // 这个是我们的答案,为了实现字典序最小
    function<void(int)> dfs = [&](int idx) {
        if (tmp.size() == a.size()) {
            // 说明我们是全部出栈了
            res.insert(tmp);
            return;
        }
        for (int i = 1; i <= 2; i++) {
            if (i == 1 && idx < a.size()) {
                // 这个是我们入栈
                st.push(a[idx]);
                dfs(idx + 1);
                st.pop();
                // 我们入栈一个, 然后向下递归
            } else if (i == 2 && !st.empty()) {
                tmp.push_back(st.top());
                st.pop();
                // 我们弹出一个
                dfs(idx);
                st.push(tmp.back());
                tmp.pop_back();
                // 我们回复现场
            }
        }
    };
    dfs(0);
    for (auto &it : res) {
        for (int i = 0; i < it.size(); i++) {
            cout << it[i] << " \n"[i == it.size() - 1];
        }
    }
    return 0;
}

时空复杂度分析

时间复杂度: $O(n!log(n!))O(n!log(n!))$

理由如下: 我们最坏的情况下, 我们需要用dfs遍历全排列的情况, 那么我们很容易可以发现就是n!的,然后我们的set的复杂度会带一个log, 所以我们最坏的情况就是$O(n!log(n!))O(n!log(n!))$

空间复杂度: $O(n\ast n!)O(n\; *\; n!)$

理由如下：我们最大会存储全排列种的情况也就是n!的情况, 然后我们每个里面有n个元素