2022-02-02:最接近的二叉搜索树值 II。 给定一个不为空的二叉搜索树和一个目标值 target,请在该二叉搜索树中找到最接近目标值 target 的 k 个值。 注意: 给定的目标值 target 是一个浮点数, 你可以默认 k 值永远是有效的,即 k ≤ 总结点数, 题目保证该二叉搜索树中只会存在一种 k 个值集合最接近目标值。 拓展: 假设该二叉搜索树是平衡的,请问您是否能在小于 O(n)(n 为总结点数)的时间复杂度内解决该问题呢? 力扣272。
答案2022-02-02:
【前驱节点-目标值】和【前驱节点-目标值】,越靠近target,就取这个节点。取了前驱节点,左扩;取了后驱节点,右扩。 准备两个栈,快速支持找前驱和后继。 时间复杂度:低于O(N)。 空间复杂度:低于O(N)。
代码用golang编写。代码如下:
package main
import "fmt"
func main() {
root := &TreeNode{val: 4}
root.left = &TreeNode{val: 2}
root.right = &TreeNode{val: 5}
root.left.left = &TreeNode{val: 1}
root.left.right = &TreeNode{val: 3}
ret := closestKValues(root, 3.713286, 2)
fmt.Println(ret)
}
type TreeNode struct {
val int
left *TreeNode
right *TreeNode
}
func NewTreeNode(val int) *TreeNode {
ans := &TreeNode{}
ans.val = val
return ans
}
// 这个解法来自讨论区的回答,最优解实现的很易懂且漂亮
func closestKValues(root *TreeNode, target float64, k int) []int {
ret := make([]int, 0)
// >=8,最近的节点,而且需要快速找后继的这么一种结构
moreTops := make([]*TreeNode, 0)
// <=8,最近的节点,而且需要快速找前驱的这么一种结构
lessTops := make([]*TreeNode, 0)
getMoreTops(root, target, &moreTops)
getLessTops(root, target, &lessTops)
if len(moreTops) > 0 && len(lessTops) > 0 && moreTops[len(moreTops)-1].val == lessTops[len(lessTops)-1].val {
getPredecessor(&lessTops)
}
for k > 0 {
k--
if len(moreTops) == 0 {
ret = append(ret, getPredecessor(&lessTops))
} else if len(lessTops) == 0 {
ret = append(ret, getSuccessor(&moreTops))
} else {
diffs := abs(float64(moreTops[len(moreTops)-1].val) - target)
diffp := abs(float64(lessTops[len(lessTops)-1].val) - target)
if diffs < diffp {
ret = append(ret, getSuccessor(&moreTops))
} else {
ret = append(ret, getPredecessor(&lessTops))
}
}
}
return ret
}
func abs(d float64) float64 {
if d < 0 {
return -d
} else {
return d
}
}
// 在root为头的树上
// 找到>=target,且最接近target的节点
// 并且找的过程中,只要某个节点x往左走了,就把x放入moreTops里
func getMoreTops(root *TreeNode, target float64, moreTops *[]*TreeNode) {
for root != nil {
if root.val == int(target) {
*moreTops = append(*moreTops, root)
break
} else if root.val > int(target) {
*moreTops = append(*moreTops, root)
root = root.left
} else {
root = root.right
}
}
}
// 在root为头的树上
// 找到<=target,且最接近target的节点
// 并且找的过程中,只要某个节点x往右走了,就把x放入lessTops里
func getLessTops(root *TreeNode, target float64, lessTops *[]*TreeNode) {
for root != nil {
if root.val == int(target) {
*lessTops = append(*lessTops, root)
break
} else if root.val < int(target) {
*lessTops = append(*lessTops, root)
root = root.right
} else {
root = root.left
}
}
}
// 返回moreTops的头部的值
// 并且调整moreTops : 为了以后能很快的找到返回节点的后继节点
func getSuccessor(moreTops *[]*TreeNode) int {
cur := (*moreTops)[len(*moreTops)-1]
*moreTops = (*moreTops)[0 : len(*moreTops)-1]
ret := cur.val
cur = cur.right
for cur != nil {
*moreTops = append(*moreTops, cur)
cur = cur.left
}
return ret
}
// 返回lessTops的头部的值
// 并且调整lessTops : 为了以后能很快的找到返回节点的前驱节点
func getPredecessor(lessTops *[]*TreeNode) int {
cur := (*lessTops)[len(*lessTops)-1]
*lessTops = (*lessTops)[0 : len(*lessTops)-1]
ret := cur.val
cur = cur.left
for cur != nil {
*lessTops = append(*lessTops, cur)
cur = cur.right
}
return ret
}
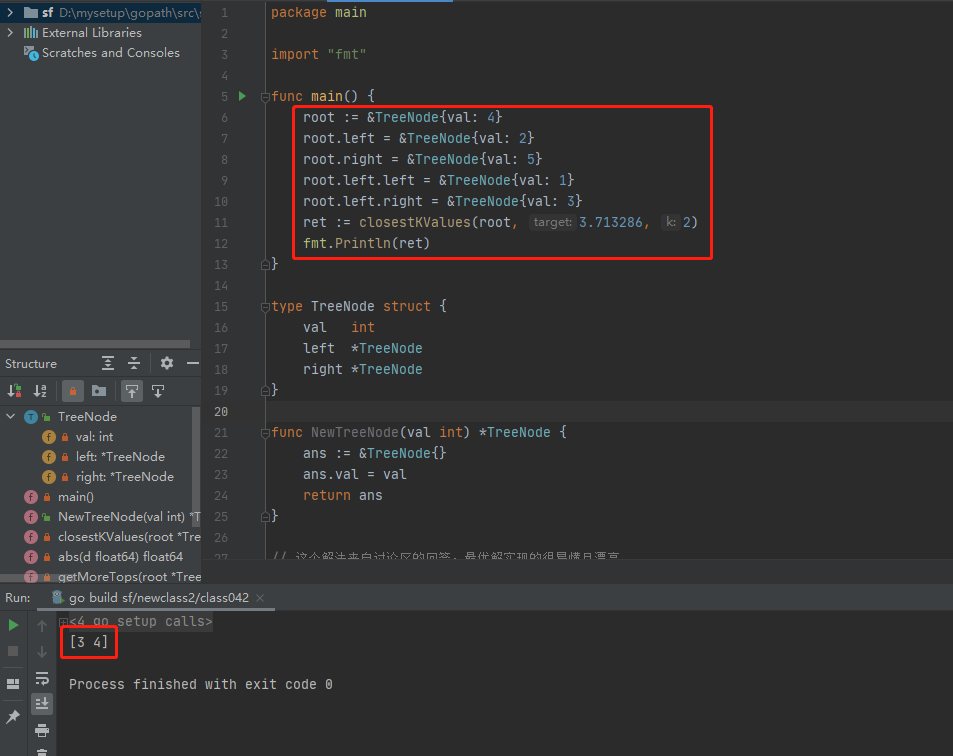
执行结果如下:






 京公网安备 11010502036488号
京公网安备 11010502036488号