题目难度: 中等
今天继续更新 Leetcode 的剑指 Offer(专项突击版)系列, 大家在公众号 算法精选 里回复
剑指offer2就能看到该系列当前连载的所有文章了, 记得关注哦~
题目描述
树可以看成是一个连通且 无环 的 无向 图。
给定往一棵 n 个节点 (节点值 1 ~ n) 的树中添加一条边后的图。添加的边的两个顶点包含在 1 到 n 中间,且这条附加的边不属于树中已存在的边。图的信息记录于长度为 n 的二维数组 edges ,edges[i] = [ai, bi] 表示图中在 ai 和 bi 之间存在一条边。
请找出一条可以删去的边,删除后可使得剩余部分是一个有着 n 个节点的树。如果有多个答案,则返回数组 edges 中最后出现的边。
示例 1:
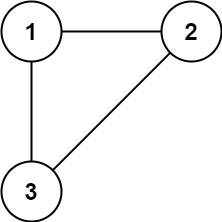
- 输入: edges = [[1,2],[1,3],[2,3]]
- 输出: [2,3]
示例 2:
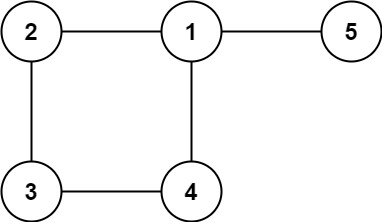
- 输入: edges = [[1,2],[2,3],[3,4],[1,4],[1,5]]
- 输出: [1,4]
提示:
- n == edges.length
- 3 <= n <= 1000
- edges[i].length == 2
- 1 <= ai < bi <= edges.length
- ai != bi
- edges 中无重复元素
- 给定的图是连通的
题目思考
- 可以使用什么数据结构或算法来解决?
解决方案
- 分析题目, n 个节点的树共有 n-1 条边, 且每个边都是有用的, 都负责将两部分连通分量连接在一起
- 所以要想找到多余的这条边, 我们可以逐个遍历每条边, 先判断其连接的两个节点是否已经连通, 是的话则说明这条边就是多余的, 否则就将这两个节点合并在一起
- 为了方便查找两个节点是否连通, 以及将它们合并在一起, 我们又可以利用最近文章中经常使用的并查集, 我之前还写过一个并查集的系列, 感兴趣的同学在我的公众号聊天框中回复 并查集 就能看到了
- 具体步骤如下:
- 首先我们需要定义一个字典 pre,
pre[x]表示 x 的祖先, 如果两个元素具有相同祖先, 就表示它们在同一个集合中. 可以把祖先pre[x]想象成一个树的根节点, 那么 x 就是树中的一个节点(可能是根节点本身) - 然后定义一个 find 方法, 查找当前元素的祖先, 如果祖先不存在的话就把自身当做祖先. 这里用到了路径压缩的优化, 就是说当发现自己的祖先不是自身的时候, 就尝试把自己的祖先设置为自己的当前祖先的祖先, 从而降低树的高度, 加快之后的查找过程.
- 最后定义一个 union 方法, 用于合并两个元素. 这里的思路也很简单, 就是找到各自的祖先, 然后将其中一个的祖先的祖先设置为另外一个祖先即可, 等于就把两个树合并在了一起
- 首先我们需要定义一个字典 pre,
- 定义好并查集后, 我们遍历所有边, 先利用 find 判断其连接的两个节点是否已经连通, 是的话就说明这条边是多余的, 直接返回即可, 否则就利用 union 将这两个节点合并在一起
- 下面的代码对必要步骤有详细的解释, 方便大家理解
复杂度
- 时间复杂度
O(NlogN): N 是节点/边的数目, 遍历所有边需要O(N)的时间, 并查集的查找和合并操作的时间复杂度是O(logN) - 空间复杂度
O(N): 并查集需要存所有 N 个节点
代码
class Solution:
def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:
### 并查集
pre = {}
def find(x):
# 查找节点x的祖先, 顺便进行路径压缩
if x not in pre:
# 当前节点x还不在pre字典中, 就初始化其祖先为节点x本身
pre[x] = x
elif pre[x] != x:
# 当前节点x和祖先不一样, 尝试路径压缩
pre[x] = find(pre[x])
return pre[x]
def union(x, y):
# 将一个节点的祖先设为另一个节点的祖先, 从而合并为同一组
pre[find(x)] = find(y)
for x, y in edges:
if find(x) == find(y):
# 如果两节点已经连通, 则说明这条边是多余的
return [x, y]
union(x, y)
return []
大家可以在下面这些地方找到我~😊
我的公众号: 算法精选, 欢迎大家扫码关注~😊





 京公网安备 11010502036488号
京公网安备 11010502036488号