蛇形矩阵

蛇形矩阵

首先我们来看问题：

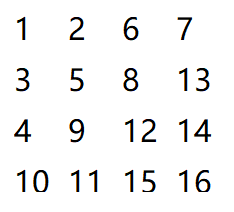
上面这个矩阵我们要怎么将它输出呢？

我们仔细观察这个矩阵，不难发现它是有一定规律的：它的数字沿着一条蛇一样弯曲排布：

那么问题来了，我们在电脑中输出都是以一行一行这样来输出的，这个矩阵的顺序明显不符合以行为参考时的输出方式，那我们就改个思路，既然不能按蛇形的顺序打印，但是我们可以按蛇形的顺序将数据存入一个数组呀，想到这里，我们就有一定方向了。 首先是写好用来存储的数组和打印函数：

#include<stdio.h>

int main()
{
    int arr[20][20] = { 0 };
    int n = 0, m = 1;
    int i = 0, j = 0, flag = 0;
    scanf("%d", &n);
    //...
     for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < n; j++)
            printf("%-2d ", arr[i][j]);
        printf("\n");
    }
    return 0;
}

接下来就可以开始我们的核心部分，数据蛇形存放： 首先我们看看这个矩阵，每一次数据蛇形的方式都是向左下方移动或者向右上方移动，我们可以以此为突破口，每一次沿左下方移动就分别令控制数组下标的i 和 j分别加加和减减，以达到向左下方或者右上方移动的目的。

while (m <= n * n)
    {
        //右上旋
        while (i >= 0 && (m <= n * n) && j <= n - 1)
        {
            arr[i][j] = m++;
            i--;
            j++;
        }
        //左下旋
        while (j >= 0 && (m <= n * n) && i <= n - 1)
        {
            arr[i][j] = m++;
            i++;
            j--;
        }
    }

然后就是要着重注意的问题是：每一次从左下旋到右上旋的转弯处的状态应该如何调整。这里要注意，位于分界线左端和右端以及分界线上的转弯状态都不同，所以要分情况，如下图：

图中的绿色方块是每一次旋转完最后一个元素处于的位置.

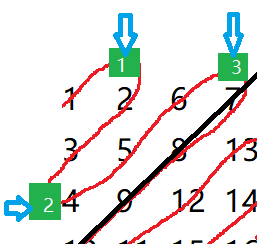
1.我们可以看到，位于分界线左半边的绿色元素，只需要每次右上旋完将纵坐标加一就可以回到下一次的起始位，如下图方块1，3；而左下旋完只需要将横坐标加一就行了，如图中绿色方块2。

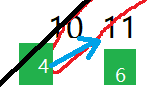
2.位于分界线上的状态，上一次是左下旋则需要横坐标加2，纵坐标加1才能返回到下一次起始位置。如下图方块4，右上旋类似：

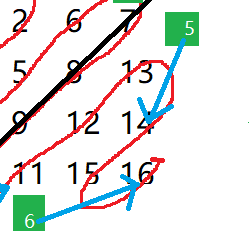
3.最后是右半边的旋转状态，这次是左下旋完需要横坐标加二，纵坐标减一，如下图方块6；而右上旋完需要纵坐标加二，横坐标减一，如下图方块5

而如何计算旋转的次数，这里我设置了一个flag变量来记录它的旋转状态，所以完整的旋转内***的：

 while (m <= n * n)
    {
        //右上旋
        while (i >= 0 && (m <= n * n) && j <= n - 1)
        {
            arr[i][j] = m++;
            i--;
            j++;
        }
        flag++;
        if (flag < n)//分界线左边
            i++;
        else if (flag == n)//分界线
        {
            i += 2;
            j--;
        }
        else//分界线右边
        {
            i += 2;
            j--;
        }
        //左下旋
        while (j >= 0 && (m <= n * n) && i <= n - 1)
        {
            arr[i][j] = m++;
            i++;
            j--;
        }
        flag++;
        if (flag < n)//分界线左边
            j++;
        else if (flag == n)//分界线
        {
            j += 2;
            i--;
        }
        else//分界线右边
        {
            i--;
            j += 2;
        }
    }

下面是我完整的解决方法：

#include<stdio.h>

int main()
{
    int arr[20][20] = { 0 };
    int n = 0, m = 1;
    int i = 0, j = 0, flag = 0;
    scanf("%d", &n);
    //思路大概是先往右上旋，然后往左下旋，再往右上旋，如此往复
    //当其碰到边界时，停止移动
    while (m <= n * n)
    {
        //右上旋
        while (i >= 0 && (m <= n * n) && j <= n - 1)
        {
            arr[i][j] = m++;
            i--;
            j++;
        }
        flag++;
        if (flag < n)
            i++;
        else if (flag == n)
        {
            i += 2;
            j--;
        }
        else
        {
            i += 2;
            j--;
        }
        //左下旋
        while (j >= 0 && (m <= n * n) && i <= n - 1)
        {
            arr[i][j] = m++;
            i++;
            j--;
        }
        flag++;
        if (flag < n)
            j++;
        else if (flag == n)
        {
            j += 2;
            i--;
        }
        else
        {
            i--;
            j += 2;
        }
    }
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < n; j++)
            printf("%-2d ", arr[i][j]);
        printf("\n");
    }
    return 0;
}

下面是我的输出结果：

n=1：

n=5：

n=9：