当 A 是对称的时候, Ax=λx 有什么特殊的呢?
1. 对称矩阵的分解
A=SΛS−1
AT=(S−1)TΛST
如果 A 是对称矩阵,也就是 A=AT。对比以上两个式子,我们可以得到 S−1=ST,也就是 STS=I,特征向量矩阵 S 是正交的。
对称矩阵具有如下的性质:
- 它们的特征值都是实数;
- 可以选取出一组标准正交的特征向量。
每个对称矩阵都可以分解为 A=QΛQ−1=QΛQT, Λ 中为实数的特征值, S=Q 中为标准正交的特征向量。
A=[1224]
A−λI=[1−λ224−λ]
det(A−λI)=(1−λ)(4−λ)−4=λ2−5λ=0
特征值和特征向量分别为:
λ1=0,x1=[2−1]
λ2=5,x2=[12]
特征向量 x1 位于零空间,特征向量 x2 位于列空间。有子空间基本定理可知,零空间正交于行空间,这里 A 是对称矩阵,所以列空间和行空间是一样的,因此两个特征向量是垂直的。而要得到标准正交向量,我们只需再除以它们各自的长度即可。所以有:
QΛQT=5 1[2−112][0005]5 1[21−12]=A
一个实对称矩阵的所有特征值都是实数。
证明
实数的共轭还是它本身,两个数积的共轭等于共轭的积,即 AB=AˉBˉ。
Ax=λx→Aˉxˉ=λˉxˉ→Axˉ=λˉxˉ(1)
对 (1) 进行转置可得
xˉTAT=λˉxˉT→xˉTA=λˉxˉT(2)
将 Ax=λx 乘以 xˉT,将 (2) 式乘以 x,可得
xˉTAx=λxˉTx(3)
xˉTAx=λˉxˉTx(4)
由于右边为向量长度的平方,因此不为零。对比 (3) 、(4) 两式可得 λˉ=λ,所以对称矩阵的特征值一定为实数。
一个实对称矩阵的所有特征向量(对应于不同特征值)是正交的。
证明
假设有 Ax=λ1x 和 Ay=λ2y,并且 λ1̸=λ2,那么
(λ1x)Ty=(Ax)Ty=xTATy=xTAy=xTλ2y
等式左边为 xTλ1y,等式右边为 xTλ2y,因为 λ1̸=λ2,所以有 xTy=0,也即两个特征向量垂直。
A=[abbc]
特征向量分别为:
x1=[bλ1−a]
x2=[λ2−cb]
x1Tx2=b(λ2−c)+b(λ1−a)=b(λ1+λ2−a−c)=0
两个特征值的和为矩阵的迹,即对角线元素的和。
我们再来看 2×2 矩阵分解后的结果
A=QΛQT=⎣⎡x1 x2⎦⎤[λ1 λ2][x1Tx2]
A=λ1x1x1T+λ2x2x2T
扩展到 n 维的情况, A=∑inλixixiT,其中每一个 xixiT 都是投影矩阵, P=xTxxxT,特征向量的长度为 1,所以分母略去了。也就是说,对称矩阵是其特征向量投影矩阵的线性组合。
2. 实矩阵的复特征向量
Ax=λx→Aˉxˉ=λˉxˉ→Axˉ=λˉxˉ
针对对称矩阵,其特征值和特征向量都是实的。但是,非对称矩阵非常容易得到虚的特征值和特征向量。在这种情况下, Ax=λx 和 Axˉ=λˉxˉ 是不同的,我们得到了一个新的特征值 λˉ 和新的特征向量 xˉ。
针对实矩阵,复数的特征值和特征向量总是一对共轭对。
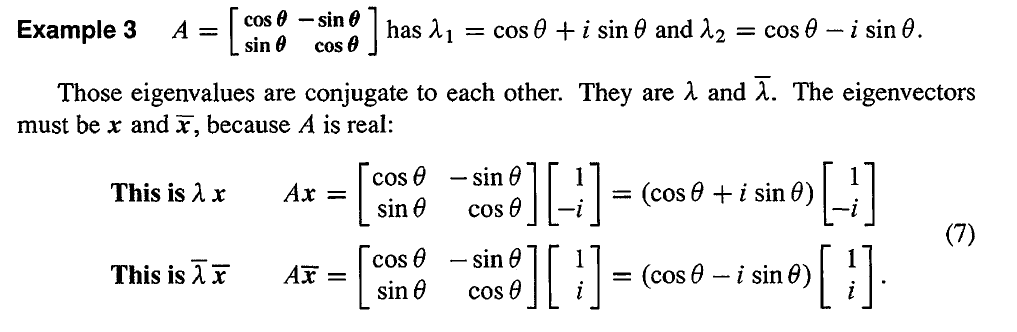
3. 特征值和主元
矩阵的主元和特征值是非常不同的,主元是通过消元得到的,而特征值是通过求解 det(A−λI)=0 得到的。到目前为止,它们唯一的联系就是:所有主元的乘积等于所有特征值的乘积,都等于矩阵的行列式值。
针对对称矩阵,还有一个隐藏的关系:主元的符号和特征值的符号一致,也就是正的主元个数等于正的特征值的个数。
证明
对称矩阵可以被分解为 A=LDLT 的形式。
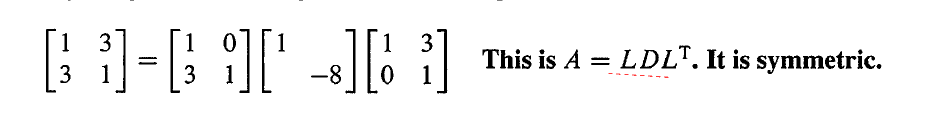
当 L 变成 I 的时候, LDLT 就变成了 IDIT,也就是由 A 变成了 D。 A 的特征值为 4 和 -2, D 的特征值为 1 和 -8。当 L 中左下角的元素从 3 变到 0 的时候, L 就变成了 I。在这个过程中,如果特征值符号发生改变的话,那肯定会有一个中间时刻,这时候特征值为 0,也就意味着矩阵是奇异的。但是最后的矩阵 D 一直有两个主元,始终是可逆的,从来不可能是奇异的,因此特征值的符号不会发生改变。
特别地,所有的特征值都大于零,也就是所有的主元都大于零,这种情况下,矩阵就称之为是正定的。
4. 重复的特征值
当没有重复特征值的时候,特征向量一定是线性不相关的,这时候矩阵一定可以被对角化。但是一个重复的特征值可能会导致特征向量的缺乏,这有些时候会发生在非对称矩阵上,但是对称矩阵一定会有足够的特征向量来进行对角化。
证明

获取更多精彩,请关注「seniusen」!




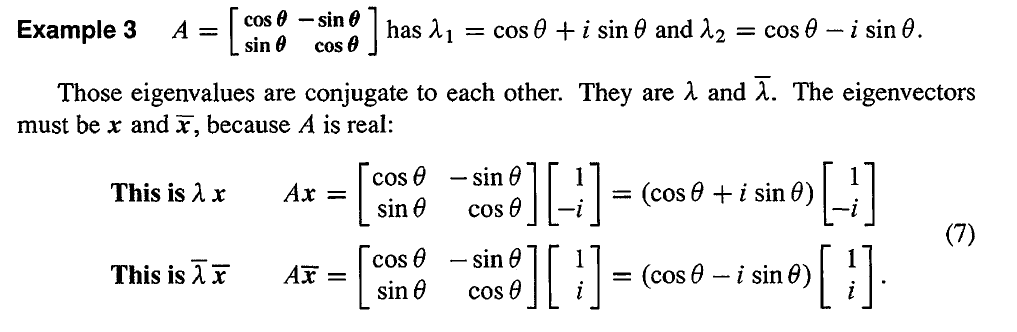



 京公网安备 11010502036488号
京公网安备 11010502036488号