文章目录
-vj链接:
https://vjudge.net/contest/256821#problem/E
A - Cake ( zoj 3537 最优三角形剖分)
看了题解一直没搞懂合并时的cost为什么是那么多,原来是这样:
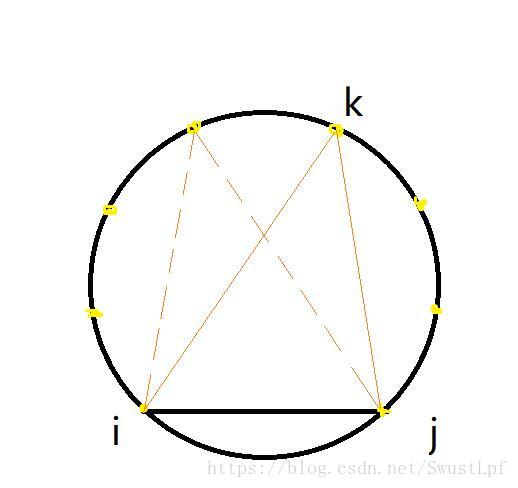
多边形不好画,就用圆代替了
dp[i][j]表示[i,j]这一段是最小值,然后就是枚举断点k,多的代价就是以i,j为底边,k为定点的这个三角形的代价,所以会多加cost[i,k]+cost[k][j],之前一直理解错了,浪费了好多时间。。。
#include"bits/stdc++.h"
using namespace std;
typedef long long LL;
const LL maxn=3e2+5;
const double eps=1e-6;
int N,MOD;
struct Point
{
double x,y;
Point() {}
Point(double x,double y):x(x),y(y) {}
};
Point P[maxn]; //装所有点
Point Convex[maxn]; //装选出来的凸包点
typedef Point Vector;
Vector operator+(Vector A,Vector B)
{
return Vector(A.x+B.x,A.y+B.y);
}
Vector operator-(Vector A,Vector B)
{
return Vector(A.x-B.x,A.y-B.y);
}
Vector operator*(Vector A,double len)
{
return Vector(A.x*len,A.y*len);
}
Vector operator/(Vector A,double len)
{
return Vector(A.x/len,A.y/len);
}
double Dot(Vector A,Vector B)
{
return A.x*B.x+A.y*B.y;
}
double Cross(Vector A,Vector B)
{
return A.x*B.y-A.y*B.x;
}
double Length(Vector A)
{
return sqrt(Dot(A,A));
}
bool cmp(Point p1,Point p2)
{
return Cross(p1-P[1],p2-P[1])>0; //就是要弄成满足逆时针这样一个一个转着走,用叉积来弄
}
int Graham(int n)//求凸包
{
int pos=1; //要赋值为第一个。。。。万一没有进入if里面,那就不晓得是个啥了。。。。WA了好多次。。。
Point tp=P[1];
for(int i=2;i<=N;i++)
{
if(P[i].y<tp.y) //只要找到一个最边边上的点就行了
{
tp=P[i];
pos=i;
}
}
swap(P[1],P[pos]);
sort(P+2,P+1+n,cmp);
Convex[1]=P[1];
Convex[2]=P[2];
int top=2;
for(int i=3;i<=n;i++)
{
while(top>=2&&Cross(Convex[top]-Convex[top-1],P[i]-Convex[top-1])<0)top--;
Convex[++top]=P[i];
}
return top;
}
int cost[maxn][maxn];
int dp[maxn][maxn];
int main()
{
while(cin>>N>>MOD)
{
for(int i=1;i<=N;i++)
{
int x,y;
cin>>x>>y;
P[i]=Point(x,y);
}
int count=Graham(N);
if(count!=N)
{
cout<<"I can't cut."<<endl;
continue;
}
for(int i=1;i<=N;i++)
{
for(int j=i+2;j<=N;j++)
{
cost[i][j]=cost[j][i]=(int)abs(P[i].x+P[j].x)*(int)abs(P[i].y+P[j].y)%MOD;
}
}
memset(dp,0x3f,sizeof dp);
for(int i=1;i<=N;i++)dp[i][i+1]=dp[i][i-1]=dp[i][i]=0;
for(int len=2;len<N;len++)
{
for(int i=1;i+len<=N;i++)
{
int j=i+len;
for(int k=i+1;k<j;k++)
{
dp[i][j]=min(dp[i][j],dp[i][k]+cost[i][k]+cost[k][j]+dp[k][j]);//以i,j作为底边,枚举[i,j]之间的点作为定点的三角形
}
}
}
cout<<dp[1][N]<<endl;
}
}
B - Halloween Costumes (light oj 1422)
题意:给n个数,代表第i天要穿颜色为 ai的衣服,衣服只能穿一次,脱下来就不能再穿了,但是阔以重着穿不脱,问最少需要多少件衣服?
dp方程感觉还是很容易理解,就是往后找一天,让这件衣服一直穿到那一天就行了,但是我写了之后发现不对,好多人都是倒着循环的,这就让我很懵逼了
按照我的理解就是:
①当a[i]==a[k]的时候,一个转移方程
②然后当a[i]不等于a[k]的时候,就应该是从两种情况转移过来呀???为什么他们只从一边转移过来都能AC呢?是数据太水还是理论上就阔以这样呀T_T
而且他们还优化一哈,直接放在k那层循环的上面了
但是我还是喜欢原始的具有意义的写法,反正能AC就行了
然后就是转移方程两种写法都行:
①:dp[i][j]=min(dp[i][j],dp[i][k-1]+dp[k+1][j])这样写表示k那一天的穿i的衣服
②:dp[i][j]=min(dp[i][j],dp[i+1][k]+dp[k+1][j])这样写表示i那天穿k的衣服(虽然这样说感觉怪怪的)
loj 蹦了。。代码应该没问题,先交上来
#include"bits/stdc++.h"
using namespace std;
typedef long long LL;
const int maxn=1e2+5;
const int MOD=1e9+7;
int dp[maxn][maxn];
int a[maxn];
int main()
{
int T;
cin>>T;
for(int Case=1; Case<=T; Case++)
{
int N;
cin>>N;
for(int i=1; i<=N; i++)cin>>a[i];
for(int i=1; i<=N; i++)for(int j=i; j<=N; j++)dp[i][j]=j-i+1; //初始化[i,j]最多需要的衣服数量
for(int len=1; len<N; len++)
{
for(int i=1; i+len<=N; i++)
{
int j=i+len;
for(int k=i+1; k<=j; k++)
{
if(a[i]==a[k])
{
dp[i][j]=min(dp[i][j],dp[i][k-1]+dp[k+1][j]);//相当于说k这天的没有了
// dp[i][j]=min(dp[i][j],dp[i+1][k]+dp[k+1][j]);//也阔以这样写
}
else
{
//else就是正常的递推,我觉得应该是两个方向对要弄吧,为什么只弄一遍就阔以AC啊?
dp[i][j]=min(dp[i][j],dp[i+1][j]+1);
dp[i][j]=min(dp[i][j],dp[i][j-1]+1);
}
}
}
}
cout<<"Case "<<Case<<": "<<dp[1][N]<<endl;
}
}
D - Coloring Brackets(codeforce 147 D)
题意:给一串括号,都是合法的状态,要给他染色,条件如下
①:一对括号只能染一个,不能都不染
②:相邻的两个括号颜色不能相同,但可以都是无***r> 求染色的方案数?
dp[i][j][k1][k2]表示[i,j]这一段,i的颜色是k1,j的颜色是k2
这道题感觉很难,即使给我说了dpdp[i][j][k1][k2]的含义我也很难自己推出来方程
大概分成两种情况来转移:
①:i和j是一对,就由[i+1,j-1]这段区间推过来
②:i和j不是一对,就找这段区间里面找i匹配的t,由[i,t],和[t+1,j]推过来
参考博客:https://blog.csdn.net/stay_accept/article/details/51338117
我把第一种情况的也改成for循环了
乘法我倒是还能理解,就是因为前面每个区间都阔以和后面的种区间对应,所以就是乘法。而为什么要找匹配点来dp呢?我感觉我还有点懵逼
噢我好像有点知道了,因为随便一个区间他如果不是完整的那他的方案数就是0,所以假如匹配的在这段区间外面,那他肯定是不完整的括号,肯定就是0了,直接不算了。
然后万一要是前面这段是完整的,后面这段不完整怎么办?比如说:()()(,现在分成了[1,2]和[3,5],后面这段不完整,那么他就是0,0乘上前面的还是0,不影响。所以只有这种()()()
[1,2]和[3,6]这种两段都是完整的才行
#include"bits/stdc++.h"
using namespace std;
typedef long long LL;
const int maxn=700+5;
const int MOD=1e9+7;
char s[maxn];
LL dp[maxn][maxn][3][3];
int main()
{
while(cin>>(s+1))
{
memset(dp,0,sizeof dp);
int N=strlen(s+1);
map<int,int>Match;
stack<int>stk;
for(int i=1; i<=N; i++) //得到匹配
{
if(s[i]=='(')stk.push(i);
else
{
int t=stk.top();
stk.pop();
Match[i]=t;
Match[t]=i;
}
}
for(int i=1; i<=N; i++)//dp初始化
{
int L=i,R=Match[i];
if(L+1==R)dp[L][R][0][1]=dp[L][R][1][0]=dp[L][R][0][2]=dp[L][R][2][0]=1;//因为一对括号只能有一边染色,所以没有[1][2]这种
}
for(int len=1; len<N; len++)
for(int i=1; i+len<=N; i++)
{
int j=i+len;
if(Match[i]==j)
{
for(int k1=0; k1<=2; k1++)
for(int k2=0; k2<=2; k2++)
{
if(k1*k2||(k1==0&&k2==0))continue; //不能都涂色 也不能两个都无色
for(int kk1=0; kk1<=2; kk1++)
for(int kk2=0; kk2<=2; kk2++)
{
if(kk1==k1&&k1!=0)continue; //左边不能相同除了0
if(kk2==k2&&k2!=0)continue; //右边不能相同除了0
dp[i][j][k1][k2]+=dp[i+1][j-1][kk1][kk2];
dp[i][j][k1][k2]%=MOD;
}
}
}
else if(Match[i]<j)
{
int t=Match[i];
for(int k1=0; k1<=2; k1++)
for(int k2=0; k2<=2; k2++)
{
for(int kk1=0; kk1<=2; kk1++)
for(int kk2=0; kk2<=2; kk2++)
{
if(k1*kk1)continue; //匹配的括号不能都有颜色
if(k1==0&&kk1==0)continue; //匹配的括号至少一个要有颜色
if(kk1==kk2&&kk1!=0)continue; //相邻的两个颜色不能相同
dp[i][j][k1][k2]+=dp[i][t][k1][kk1]*dp[t+1][j][kk2][k2]%MOD;//前面一段区间的每一种情况都阔以对应后面区间的每一种情况,所以是乘法
dp[i][j][k1][k2]%=MOD;
}
}
}
}
LL ans=0;
for(int k1=0; k1<=2; k1++)
for(int k2=0; k2<=2; k2++)
{
ans+=dp[1][N][k1][k2];
ans%=MOD;
}
cout<<ans<<endl;
}
}
E - Multiplication Puzzle (poj 1651 矩阵连乘)
以前做过矩阵连乘的问题,这道题推着推着突然发现不就是矩阵连乘的问题么。。。
但是感觉理解得不深入,又重新理解了好久。
dp[i][j]表示第i个数到第j个数这样连乘的最优答案
同样是枚举断点k,然后 dp[i][j]=dp[i][k]+cost+dp[k][j]
这一步都是套路没毛病,但是这个cost的计算就有点懵逼 cost=a[i]⋅a[k]⋅a[j]
先来看个例子:
a1 a2 a3 a4 a5 a6 a7 a8 a9
我没枚举k=5的时候实际上是,1 2 3 4 5已经乘完了,变成了一个 a1∗a5的矩阵了,也就是dp[1][5]
同理dp[5][9]也是一个 a5∗a9的矩阵了
这样才能有个 a1∗a5 的矩阵 乘一个 a5∗a9的矩阵
我之前就一直觉得为什么不是dp[i][k-1]+cost+dp[k+1][j],就是因为这样
#include"iostream"
#include"cstring"
using namespace std;
typedef long long LL;
const int maxn=1e2+5;
const int MOD=1e9+7;
int dp[maxn][maxn];
int a[maxn];
int main()
{
int N;
while(cin>>N)
{
memset(dp,0x3f,sizeof dp);
for(int i=1; i<=N; i++)cin>>a[i];
for(int len=0; len<N; len++)
{
for(int i=1; i+len<=N; i++)
{
int j=i+len;
if(j-i+1<=2)dp[i][j]=dp[j][i]=0;//如果小于三个数,那肯定不能构成矩阵的乘法
else for(int k=i+1; k<=j-1; k++)dp[i][j]=min(dp[i][j],dp[i][k]+a[i]*a[k]*a[j]+dp[k][j]);
}
}
cout<<dp[1][N]<<endl;
}
}
F - Food Delivery (zoj 3469)
参考博客:https://blog.csdn.net/wr132/article/details/51182546
题意是说有一个外卖小哥要去送外卖,有n个待送的地方,每个地方都有一个不高兴的值,然后外卖小哥会得到这个 不高兴值 乘 送到的时间,求最后外卖小哥得到的最小值是多少?
因为送完一个地方后,要么去送左边没送过的第一个,要么去右边没送过的第一个,,这两个肯定是最小的两个了,其他的比他们都大,所以开第三维表示最后送的地方是在左边还是右边都还好理解,但是区间dp最关键的合并cost那里这道题对我来说感觉很难理解
假如说送第一个人的时间是 t1,花费是 v1,假如有三个位置,那么总的花费就是: cost=a1⋅t1+a2⋅(t1+t2)+a3⋅(t1+t2+t3)
变个形就是: cost=(a1+a2+a3)⋅t1+(a2+a3)⋅t2+a3⋅t3
这个式子就是我们计算cost的式子,比如第一个时间计算的花费,不仅有他自己的 a1,还有还在等待的 a2+a3,同理,第二段时间,不仅有他自己的花费 a2,还有还需要等待的 a3
但是这样子dp感觉就没有中间dp的含义了啊,比如中间随便一个区间,dp并不能够表示这段区间的最小花费啊,一切都是为了最后的总区间做贡献,所以感觉怪怪的~
#include"bits/stdc++.h"
using namespace std;
typedef long long LL;
const int maxn=1e3+5;
const int MOD=1e9+7;
int dp[maxn][maxn][2];
struct AAA
{
int pos,v;
bool operator<(const AAA tp)const
{
return pos<tp.pos;
}
};
AAA a[maxn<<1];
int sum[maxn];
int abss(int n)
{
if(n<0)return -n;
else return n;
}
int N,V,X;
int cost(int i,int j,int st,int en)//i左边,j右边,这次是从st送到en
{
//计算代价是i左边的 + j右边的 + 他本身的
return (sum[i-1]+sum[N]-sum[j]+a[en].v)*abss(a[st].pos-a[en].pos);
}
int main()
{
while(cin>>N>>V>>X)
{
AAA t;
t.pos=X;
t.v=0;
a[0]=t;
for(int i=1; i<=N; i++)cin>>a[i].pos>>a[i].v;
sort(a,a+1+N);
sum[-1]=0;
for(int i=0; i<=N; i++)sum[i]=sum[i-1]+a[i].v;
int pos=lower_bound(a,a+1+N,t)-a;
memset(dp,0x3f,sizeof dp);
dp[pos][pos][0]=dp[pos][pos][1]=0;
for(int i=pos;i>=0;i--)
for(int j=pos;j<=N;j++)
{
//送到i的
dp[i][j][0]=min(dp[i][j][0],dp[i+1][j][1] + cost(i,j,j,i));//从j送过来
dp[i][j][0]=min(dp[i][j][0],dp[i+1][j][0] + cost(i,j,i+1,i));//从i+1送过来
//送到j的
dp[i][j][1]=min(dp[i][j][1],dp[i][j-1][0]+cost(i,j,i,j));//从i送过来
dp[i][j][1]=min(dp[i][j][1],dp[i][j-1][1]+cost(i,j,j-1,j));//从j-1送过来
}
cout<<(LL)min(dp[0][N][0],dp[0][N][1])*V<<endl;
}
}
G - You Are the One (hdu 4283)
题意就是说有n个diaosi要上台表演(这题题目是you are the one 哈哈哈哈),第i个人有个unhappy值是a[i]乘上排他前面的人数,求最小的总unhappy值
如果题目就这样的话肯定就会想到把unhappy值大的放在最前面,但是现在有个限制条件就是,顺序不能随便换,而是只能通过一个栈来换
不知道大佬们怎么就想到区间dp了的T_T
用dp[i][j]表示序号从i到j的人排在最前面,就是说前面没有人,我本来想的是dp[i][j]就表示从i到j的值,然后第i个人换到k的位置,那么前面[i+1,k]的人的unhappy值会减少,但是这样我没有推出来,看网上的博客好像都是这种前面没有人的做法
举个例子:
1 2 3 4 5 6 7 8
我们在计算dp[2][6]的时候就是计算 2 3 4 5 6 这个序列的值,前面没有1 了
假如说现在枚举的k=4,就是说变成了 3 4 2 5 6
就要拆成3个部分来算
3 4
x x 2
x x x 5 6
其中 3 4 这个序列的值就是dp[3][4]
而 x x 2 的值前面有 4-2个人 就是 a[2] * (4-2)
然后 x x x 5 6 的值就是 前面有 4-2+1个人,所以这些人每个人都要等待4-2+1次,所以就是dp[5][6]+sum[5,6]*(4-2+1)
#include"bits/stdc++.h"
using namespace std;
typedef long long LL;
const int maxn=1e2+5;
const int inf=1e9;
int a[maxn],sum[maxn];
int dp[maxn][maxn];//dp[i][j]表示[i,j]这一段是放在最前面的情况
int main()
{
int T;
cin>>T;
for(int Case=1;Case<=T;Case++)
{
memset(dp,0,sizeof dp);
int N;
cin>>N;
for(int i=1;i<=N;i++)
{
scanf("%d",a+i);
sum[i]=sum[i-1]+a[i];
}
for(int len=1;len<N;len++)
{
for(int i=1;i+len<=N;i++)
{
int j=i+len;
dp[i][j]=inf;
for(int k=i;k<=j;k++)//k从i开始枚举是因为i作为第一个有可能就是最优的
{
dp[i][j]=min(dp[i][j],dp[i+1][k]+a[i]*(k-i)+dp[k+1][j]+(k-i+1)*(sum[j]-sum[k]));
}
}
}
cout<<"Case #"<<Case<<": "<<dp[1][N]<<endl;
}
}
H - String painter(hdu 2476)
题意:给两个串,要把第一个串变成第二个串。一次操作只能把一段区间变成同样的字符,问最少需要几次操作?
这道题感觉是上面B题(light oj 1422)的增强型啊,他先要求一哈从白的图成这样的dp[i][j],然后还要再弄一个一维的区间dp…感觉很牛皮~
感觉这个二维的dp就是为后面的一维dp服务的~
#include"bits/stdc++.h"
using namespace std;
typedef long long LL;
const int maxn=1e2+5;
const int MOD=1e9+7;
int dp[maxn][maxn];
char s1[maxn],s2[maxn];
int ans[maxn];
int main()
{
while(cin>>(s1+1)>>(s2+1))
{
int N;
N=strlen(s1+1);
for(int i=1; i<=N; i++)for(int j=i; j<=N; j++)dp[i][j]=j-i+1; //初始化[i,j]最多需要的次数
for(int len=1; len<N; len++) //求dp[i][j]这一步跟light oj 1422一样
{
for(int i=1; i+len<=N; i++)
{
int j=i+len;
for(int k=i+1; k<=j; k++)
{
if(s2[i]==s2[k])
{
// dp[i][j]=min(dp[i][j],dp[i][k-1]+dp[k+1][j]);//k这一格阔以根i一起刷
dp[i][j]=min(dp[i][j],dp[i+1][k]+dp[k+1][j]);
}
else //否则就正常递推下去
{
dp[i][j]=min(dp[i][j],dp[i+1][j]+1);
dp[i][j]=min(dp[i][j],dp[i][j-1]+1);
}
}
}
}
for(int i=1; i<=N; i++)ans[i]=dp[1][i];
for(int i=1; i<=N; i++)
{
if(s1[i]==s2[i])ans[i]=ans[i-1];//如果相等,那么就阔以少刷一次
else //否则枚举断点找最优的
{
for(int k=1; k<i; k++)ans[i]=min(ans[i],ans[k]+dp[k+1][i]);
}
}
cout<<ans[N]<<endl;
}
}




 京公网安备 11010502036488号
京公网安备 11010502036488号