CodeVS3044 矩形面积求并

http://codevs.cn/problem/3044/
题意：在 $100000 * 100000$ 的坐标上输入n个矩形，边长为实数，求这些矩形的并的面积。
思路：扫描线线段树，黄学长讲的非常好：http://hzwer.com/879.html
大致记录一下：对所有x坐标离散化，对x坐标建一颗线段树，在下边界加入，上边界删去。按照y坐标从小到大的顺序，依次处理所有相邻y坐标夹的子矩形，矩形的高就是 $y_{1} - y_{2}$ ,长是所有被覆盖的x的段。注意线段树维护的是x轴上的边，而不是孤立的点。举个例子，x坐标是1，2，3，4，现在[1,3]增加，划分为[1,2]和[3,3]，如果维护点，就只有 $1 - 2$ ，而没有 $2 - 3$ ，规定边i连接点i和i+1，应该[1,3]增加变成边[1,2]增加，线段树maintain里边也要做修改。
还有要注意这个线段树不需要pushdown的原因是：一段+1后，即使它的子段-1，这段一定还都被覆盖，因为还没到这个大段-1的时候。
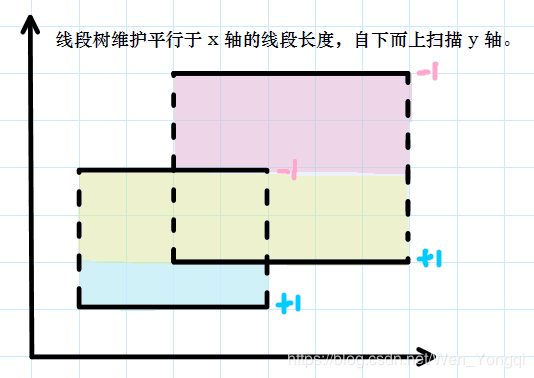
盗一张图（来自https://www.cnblogs.com/milky-w/p/8426772.html）

#include<bits/stdc++.h>
using namespace std;
#define maxn (100000+100)

int n;
double hash[maxn*2];
struct Query{
    double x1,x2,y;
    int flag;
    bool operator < (Query x)const{
        return y<x.y;
    }
}Q[maxn*2];
int ql,qr,val,col[maxn*8];
double sumv[maxn*8];
double ans;

void maintain(int o,int l,int r)
{
    if(col[o])sumv[o]=hash[r+1]-hash[l];
    else if(l==r)sumv[o]=0;
    else sumv[o]=sumv[o*2]+sumv[o*2+1];
}

void update(int o,int l,int r)
{
    if(ql<=l&&qr>=r)col[o]+=val;
    else
    {
        int mid=(l+r)/2;
        if(ql<=mid)update(o*2,l,mid);
        if(qr>mid)update(o*2+1,mid+1,r);
    }
    maintain(o,l,r);
}

int main()
{
    //freopen("input.in","r",stdin);
    while(cin>>n && n)
    {
        ans=0;
        memset(sumv,0,sizeof(sumv));
        memset(col,0,sizeof(col));
        double x1,x2,y1,y2;
        for(int i=1;i<=n;i++)
        {
            scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);
            Q[i*2-1].x1=Q[i*2].x1=x1;
            Q[i*2-1].x2=Q[i*2].x2=x2;
            Q[i*2-1].y=y1;Q[i*2-1].flag=1;
            Q[i*2].y=y2;Q[i*2].flag=-1;
            hash[i*2-1]=x1;hash[i*2]=x2;
        }
        sort(Q+1,Q+1+2*n);sort(hash+1,hash+1+2*n);
        for(int i=1;i<=2*n;i++)
        {
            ql=lower_bound(hash+1,hash+2*n+1,Q[i].x1)-hash;
            qr=lower_bound(hash+1,hash+2*n+1,Q[i].x2)-hash-1;
            val=Q[i].flag;
            update(1,1,2*n);
            ans+=sumv[1]*(Q[i+1].y-Q[i].y);
        }
        printf("%.2f\n",ans);
    }
    return 0;
}