描述
题目描述
首先给定我们一个字符串和一个数组,问我们是否可以把字符串拆解成若干子串,并且这些子串都可以在我们的数组种找到
当然这个问题我们也可以转换成为是否可以用数组中的若干项组成我们的字符串
样例解释
首先给定我们这样的一个输入
"nowcoder",["no","wcod","der"]
首先我们可以把这个, 我们可以分解为, 然后我们可以发现我们可以在我们的数组里面找到,所以这个可以继续进行,然后我们把字符串变成了,然后我们看我们是否可以把分解然后找到可以在数组中出现的,但是我们发现假设我们把如果分解成那么我们剩下的就是,我们可以发现我们无法构成,所以我们最后返回的就是
所以我们的输出是
false
题解
解法一:Trie + dfs + 剪枝
解题思路
首先我们想,他给了我们这么多的单词,我们最先的想法是什么,是不是建造一颗字典树,然后我们把我们的单词的数组在字典树上建立出来,然后我们每次去dfs我们的这个字符串去看看是否可以在我们的字典树上找出来,那么我们就是建树 + dfs,这里我们最好剪枝一下,这样我们可以减少很多重复的一个操作
代码实现
class Solution {
int nex[2020][26], cnt = 0;
bitset<2020> exist = 0, failIndex = 0;
// nex是用于存这颗字典树的,cnt表示节点的编号
// exist用于判断是否存在以这个点结尾的单词
// failIndex是我们用于剪枝的一个操作,用来存储我们从某一个点开始不满足的点
public:
void insert(string s) {
int p = 0;
// 树的节点下表
for (auto &it : s) {
// 遍历这个字符串
int c = it - 'a';
// 把字母转换成为0 - 25
if (!nex[p][c]) nex[p][c] = ++cnt;
// 如果我们之后下一个点没有存储东西,那么我们把这个点用上
p = nex[p][c];
// 我们的指针指向下一个点
}
exist[p] = 1;
// 标记一下这个点是作为了一个字符串的结尾
}
bool dfs(string s, int pos) {
// 用于搜索我们从第pos位开始的s字符串
if (failIndex[pos] == 1) return false;
// 如果当前的这个位置已经是确定不可以的,我们直接剪枝
if (pos == s.size()) return true;
// 如果到了最后的一位,我们也是直接剪枝
int p = 0;
// 跟我们添加字符串一样的操作
for (int i = pos; i < s.size(); i++) {
// 遍历我们从起始位置到最后的字符串
int c = s[i] - 'a';
// 转换为0 - 25
if (!nex[p][c]) break;
// 如果不存在这个点,说明我们之前的这个字符串不行
p = nex[p][c];
// 否则移动到下一个点
if (exist[p] and dfs(s, i + 1)) return true;
// 如果有以这个点为结尾的字符串,然后我们去搜索下一位开始的字符串
}
failIndex[pos] = 1;
// 这点不可以我们返回了false,标记上
return false;
}
bool wordDiv(string s, vector<string>& dic) {
for (auto &it : dic) insert(it);
// 进行建树存储的一个过程
return dfs(s, 0);
// 搜整个s串
}
};
图解代码:字典树的讲解
这里我们讲一下字典树的构建,什么是字典树,说白了,就是把我们的字符串放到我们的树上进行一个操作,比如我们的第一个样例["now","coder"], 我们建树之后是什么样子呢?如下图所示
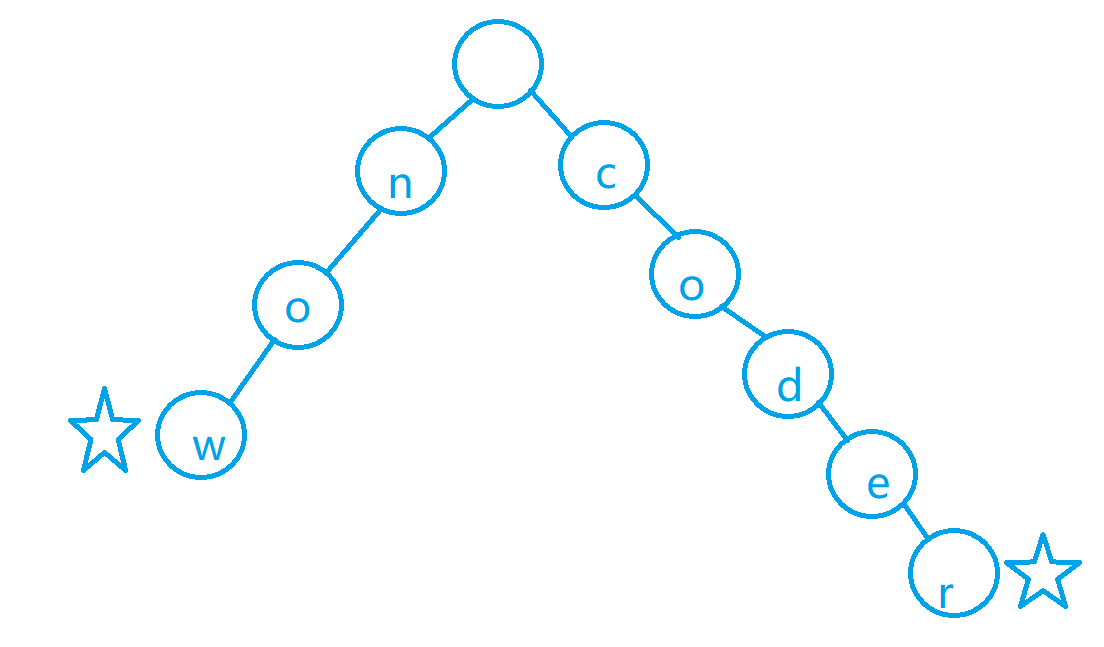
这里其实我们很容易的就是发现了,我们可以发现其实所谓字典树就是我们把我们的每一个单词,变成树上的一个树枝,然后我们在字符串的末尾打上一个标记,就是我图中的五角星,避免有重复的,这样我们的树就构建好了,我们每次dfs看我们以某一个位置开始的是否可以在这颗树中找到即可
时空复杂度:
时间复杂度:
理由如下:首先依照我们的这个算法,我们先是字典树的建树,我们题中规定了我们数组的长度为,然后我们数组中的每一个字符串的长度为,那么我们建树的时候时间复杂度就是,然后我们对我们的输入的字符串每一位进行dfs的时候,我们每一位最后是遍历字典树上最长的那一个单词,也就是,然后根据数据范围,我们可以明显发现,我们的是远小于的所以,我们最后的时间复杂度就是
空间复杂度:
理由如下:首先我们可以考虑我们建树的时候一共最多是会出现这些的点数,那么我们会需要这么大的一个空间,然后我们用于判断每一个点的时候我们需要开两个bool数组,这里我使用了bitset进行了一个优化,然后我们因为有26个英文字母,那么我们其实是开的静态数组,实际上的空间要使用的就是,考虑到复杂度中不带有常数,那么我们最后的空间复杂度就是,这里其实我们开静态数组的速度会快了很多,但是事实上我们有很多的空间造成了浪费
解法二:动态规划
解题思路
首先这个DP我们如何去思考,假设我们从前向后递推,如果我们第位是我们的判断是否从是可以满足在我们的字典数组里面找到的,然后那我们下一位怎么办呢?比如我们到了第位,我们是不是就是看之前的位置有没有dp数组是满足条件的,然后比如我们第位的DP数组是满足条件的,那么我们就是去看我们的从第位到我们的第位是否是一个可以在我们的字符串的字典里面找到的,如果可以找到的话,那我们这个就是的,找到满足的时候我们就可以直接去找第位,可以仔细看一下代码里面的注释
代码实现
class Solution {
public:
bool wordDiv(string s, vector<string>& dic) {
unordered_set<string> st;
for (auto &it : dic) st.insert(it);
// 用于存储出现过的字符串
int len = s.size();
// 获取字符串
bitset<510> dp = 0;
// 这里用bitset代替bool数组,不论是空间还是时间上效率更高
dp[0] = 1;
// 我们第一位就是一个字符串都没有的时候我们默认是可以的
for (int i = 1; i <= len; i++) {
// 我们遍历之后的每一位
for (int j = 0; j < i; j++) {
// 我们判断截取多少位是可以的
if (dp[j] and st.find(s.substr(j, i - j)) != st.end()) {
// 这里我们判断如果前j位是可以的,然后后面的也是出现过的单词
dp[i] = 1;
// 我们直接标成可以
break;
// 我们就不用再继续比较了
}
}
}
return dp[len];
// 返回我们最后的是否是可以整个字符串都可以构成
}
};
时空复杂度
时间复杂度:
理由如下: 我们的是字符串的一个长度,然后我们一共会有个状态需要判断,所以我们每一个点位都是要进行一个枚举,那么我们就是的时间复杂度
空间复杂度:
理由如下:我们所花费的空间一个是dp的数组,一个是我们的哈希表,最多是个字符串,这里我们这里使用bitset代替了我们的bool数组,这里我们可能时间复杂度上面没有什么区别,但是实际上我们的常数是要更小的,bitset可以把时间和空间都做到一个很棒的优化,一般我会拿这个代替bool数组
关于bitset
大家可以看一下我这篇牛客题目的题解 bitset的传送门






 京公网安备 11010502036488号
京公网安备 11010502036488号