文章目录
1. 树的定义
树(Tree):n(n≥0)个结点构成的有限集合
当 n=0 时,称为空树
1. 特征
对于任一棵非空树(n>0),它具备以下特征:
- 树中有个称为“根(Root)”的特殊结点,用 r 表示
- 其余结点可分为 m(m>0) 个互不相交的有限集 T 1, T 2,…, T m,其中每个集合本身又是一棵树,称为原来树的"子树(SubTree)"
- 子树是不相交的
- 除根结点外,每个结点有且仅有一个父结点
- 一棵 N 个结点的树有 N-1 条边
2. 基本术语
- 结点的度(Degree):结点的子树个数
- 树的度:树的所有结点中最大的度数
- 叶结点(Leaf):度为 0 的结点
- 父结点(Parent):有子树的结点是其子树的根结点的父结点
- 子结点(Child):若 A 结点是 B 结点的父结点,则称 B 结点是 A 结点的子结点,也称孩子结点
- 兄弟结点(Sibling):具有同一父结点的各个结点彼此是兄弟结点
- 路径:从结点 n 1 到 n k 的路径为一个结点序列 n 1,n 2,…,n k,n i 是 n i+1 的父结点
- 路径长度:路径所包含边的个数
- 祖先结点(Ancestor):沿树根到某一结点路径上的所有结点都是这个结点的祖先结点
- 子孙结点(Descendant):某一结点的子树中的所有结点是这个结点的子孙
- 结点的层次(Level):规定根结点在 1 层,其他任一结点的层数是其父结点的层数加一
- 树的深度(Depth):树中所有结点中的最大层次是这棵树的深度
3. 树的表示
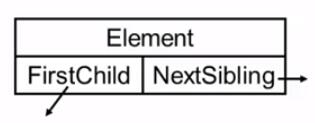
1. 儿子-兄弟表示法
- Element 存值
- FirstChild 指向第一个儿子
- NextSibling 指向下一个兄弟
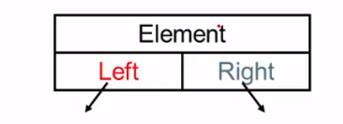
2. 二叉树
即度为 2 的树
- Element 存值
- Left 指向左子树
- Right 指向右子树
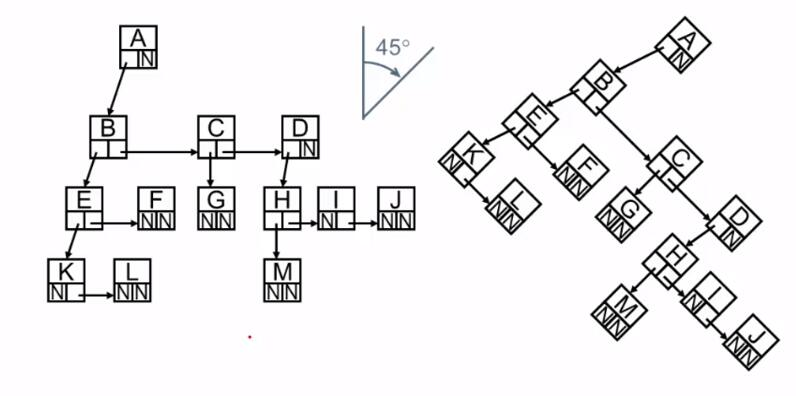
二叉树其实就是儿子-兄弟表示法的链表右移 45° 得到的结果
2. 二叉树
1. 定义
二叉树 T:一个有穷的结点集合
这个集合可以为空
若不为空,则它是由根结点和称为其左子树T L和右子树T R的两个不相交的二叉树组成
二叉树的子树有左右顺序之分
2. 五种基本形态
3. 特殊形态
-
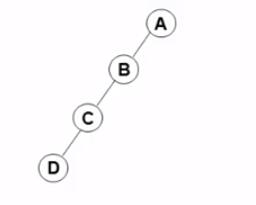
斜二叉树
只有左儿子或只有右儿子
-
完美二叉树(满二叉树)
除最后一层叶结点外,每个结点都有两个子结点
-
完全二叉树
有 n 个结点的二叉树,对树中结点按从上至下、从左到右顺序进行编号,编号为 i(1 ≤ i ≤ n)结点与满二叉树中编号为 i 结点在二叉树中位置相同
4. 重要性质
- 一个二叉树第 i 层的最大结点数为:2 i−1,i ≥ 1
- 深度为 k 的二叉树有最大结点总数为:2 k -1,k ≥ 1
- 对任何非空二叉树 T,若 n 0 表示叶结点的个数、n 2 是度为 2 的非叶结点个数,那么二者满足关系 n 0 = n 2 +1
5. 抽象数据类型定义
-
类型名称:二叉树
-
数据对象集:一个有穷的结点集合,若不为空,则由根结点和其左、右二叉子树组成
-
操作集:BT ∈ BinTree,Item ∈ ElementType
主要操作有:
Boolean IsEmpty(BinTree BT):判别 BT 是否为空void Traversal(BinTree BT):遍历,按某顺序访问每个结点BinTree CreatBinTree():创建一个二叉树
常用的遍历方法有:
void PreOrderTraversal(BinTree BT):先序——根、左子树、右子树void InOrderTraversal(BinTree BT):中序——左子树、根、右子树void PostOrderTraversal(BinTree BT):后序——左子树、右子树、根void LevelOrderTraversal(BinTree BT):层次遍历,从上到下、从左到右
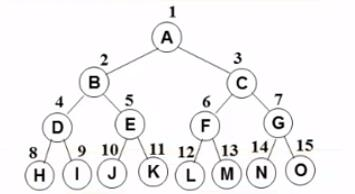
1. 顺序存储结构
按从上至下、从左到右顺序存储 n 个结点的完全二叉树的结点父子关系:
- 非根结点(序号 i > 1)的父结点的序号是 ⌊i/2⌋(向下取整)
- 结点(序号为 i)的左孩子结点的序号是 2i(若 2 i ≤ n,否则没有左孩子
- 结点(序号为 i)的右孩子结点的序号是 2i+1(若 2 i +1 ≤ n,否则没有右孩子
2. 链表存储
typedef struct TreeNode *BinTree;
struct TreeNode{
Element Data; // 存值
BinTree Left; // 左儿子结点
BinTree Right; // 右儿子结点
};









 京公网安备 11010502036488号
京公网安备 11010502036488号