题目地址：https://ac.nowcoder.com/acm/contest/551/C

题目：

给出字符串长度n和k，求字符串中长度≥k的不同子串数目

 

解题思路：

用到后缀数组算法中的height数组，height[i]表示排名第i的后缀字符串和第i-1名的后缀字符串的最长公共前缀长度，如图：

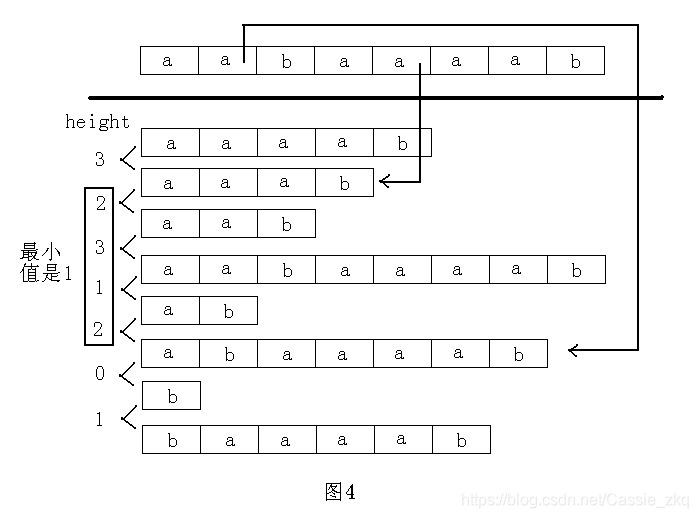
若要求不同的子串数目，每个后缀字符串ss对结果的贡献都是len(ss)-它对应的height[]值（减去重复的子串）

若要求长度≥k的不同子串数目，每个后缀字符串ss对结果的贡献都是len(ss)-max(它对应的height[]值, k-1)，可能k-1的长度大于height的长度，相当于在减去重复的子串的基础上再减去长度<k的子串，对结果的贡献不能是负数，再与0比较去较大值。

⚠️结果用long long 存

 

ac代码：

#include <bits/stdc++.h>
using namespace std;
const int maxn = 100010;
//不能声明ws，保留字
int sa[maxn], rankk[maxn], height[maxn], wv[maxn], wss[maxn], wa[maxn], wb[maxn], r[maxn];
char s[maxn];
bool cmp(int *r, int a, int b, int l)
{
    return r[a] == r[b] && r[a + l] == r[b + l];
}
//O(nlogn)
void get_sa(int *r, int *sa, int n, int m)
{
    int *x=wa, *y=wb;
    int p =0, i, j;
    for(i = 0; i < m; i++) wss[i] = 0;
    for(i = 0; i < n; i++) wss[ x[i]=r[i] ]++;
    for(i = 1; i <= m; i++) wss[i] += wss[i - 1];
    for(i = n - 1; i >= 0; i--) sa[--wss[x[i]]] = i;
    for(j = 1, p = 1; p < n; j *= 2, m = p)
    {
        //对第二关键字排序
        for(p = 0, i = n - j; i < n; i++) // [n-j,n)没有内容
            y[p++] = i;
        for(i = 0; i < n; i++)
            if(sa[i] >= j) y[p++] = sa[i] - j;
        //对字符串排序
        for(i = 0; i < n; i++) wv[i] = x[y[i]]; //排名为i的第二关键字对应的第一关键字的排名，x此时相当于rankk，y相当于第二关键字的sa
        for(i = 0; i < m; i++) wss[i] = 0;
        for(i = 0; i < n; i++) wss[wv[i]]++;
        for(i = 1; i <= m; i++) wss[i] += wss[i - 1];
        for(i = n - 1; i >= 0; i--) sa[--wss[wv[i]]] = y[i];
        //相同的字符串排名相同
        swap(x,y);
        for(i = 1, p = 1, x[sa[0]] = 0; i < n; i++)
            x[sa[i]] = cmp(y, sa[i-1], sa[i], j) ? p - 1 : p++;
    }
}
//O(n)
void get_height(int n)
{
    int k = 0;
    for(int i = 1; i <= n; i++) rankk[sa[i]] = i;
    for(int i = 0; i < n; i++)
    {
        k ? k-- : 0;//根据性质height[rank[i]] ≥ (height[rank[i-1]] -1)
        int j = sa[rankk[i] - 1];//上一名的开始下标
        while(r[i + k] == r[j + k]) k++;
        height[rankk[i]] = k;
    }
}
int main()
{
    //freopen("/Users/zhangkanqi/Desktop/11.txt","r",stdin);
    int n, m, Size = 255;
    long long ans = 0;
    scanf("%d %d", &n, &m);
    scanf("%s",s);
    for(int i = 0; i < n; i++)
        r[i] = (int)s[i];
    r[n] = 0;
    get_sa(r, sa, n + 1, Size);
    get_height(n);
    for(int i = 1; i <= n; i++)
        ans += max(0,n - sa[i] - max(m - 1, height[i]));
    printf("%lld\n", ans);
    return 0;
}