描述

题目描述

给我们一个n个节点的二叉树，然后让我们修建二叉树，最后返回我们修建过后的二叉树

修建规则如下：

不能直接删除叶子节点，可以删掉叶子节点的父亲节点，然后叶子节点和父亲节点都没了 想尽可能多的留下节点，让我们输出最后的叶子节点

样例解释

{1,1,1,1,1,1,1}

如果我们想要删掉最下面的四个节点的话，我们要做这么一个事情，把下面四个叶子节点的父节点都删掉

所以最后我们只剩下一个根节点，所以最后的答案为

{1}

题解

二叉树介绍

这里简单讲解一下最基本的二叉树，让大家对输入的一个数组是如何变成一颗二叉树有一个基本的概念

首先我们拿示例二举例子

示例二的输入为

{1,#,1,#,1,#,1,#,1}

然后我们把这颗树画出来

所以我们要删除最下面的叶子节点的话，我们就是删除掉叶子节点的父亲节点，所以我们最后剩下的是这样一颗树

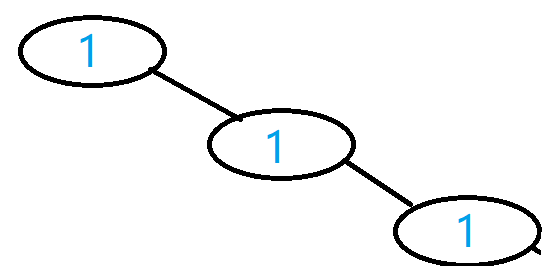
然后我们如何用一个数组表示一个二叉树呢？

假设我们的数组设置为a，那么我们用 a[1] 来表示我们的根节点，那么我们的 a[1 * 2] 则为我们的根节点的左儿子， a[1 * 2 + 1] 为根节点的右儿子，其他节点也是如此，我们可以把1换成x，这样我们便理解了如何用一个数组来表示二叉树

解法一：C++

解题思路

我们直接一直向下递归，如果发现这个节点是空的，我们删掉，如果这个节点的左孩子是叶子节点，我们删掉，如果这个节点的右孩子是叶子节点我们删掉

代码实现

class Solution {
public:
    TreeNode* pruneLeaves(TreeNode* root) {
        if (root == nullptr) return nullptr;
//         当前点为空
        if (root->right != nullptr && root->right->left == nullptr && root->right->right == nullptr) return nullptr;
//         右节点是叶子节点
        if (root->left != nullptr && root->left->left == nullptr && root->left->right == nullptr) return nullptr;
//         左节点是叶子节点
        root->left = pruneLeaves(root->left);
//         递归左孩子
        root->right = pruneLeaves(root->right);
//         递归右孩子
        return root;
    }
};

时空复杂度

时间复杂度： $O(n)O(n)$

理由如下：我们可以发现这么一个问题，我们在遍历整个树的时候，我们每一个点只会进去一次，然后出去一次，所以最后我们是走了$2\ast n2\; *\; n$个点，所以最后的时间复杂度就是$O(n)O(n)$

空间复杂度： $O(n)O(n)$

理由如下：因为使用的二叉树深度的一个递归栈，根据二叉树的性质，一般情况下，我们的深度是$O(logn)O(logn)$，但是在极限的情况下，我们的树退化成为了一条链，那么我们的深度就是$O(n)O(n)$，所以我们的空间复杂度应该是$O(n)O(n)$

解法二：Java

解题思路：

暴力向下递归，然后我们删掉最下层叶子节点的父亲节点

代码实现：

import java.util.*;

public class Solution {
    public TreeNode pruneLeaves (TreeNode root) {
        if (root == null) return null;
//         当前点为空
        if (root.right != null && root.right.left == null && root.right.right == null) return null;
//         右节点是叶子节点
        if (root.left != null && root.left.left == null && root.left.right == null) return null;
//         左节点是叶子节点
        root.left = pruneLeaves(root.left);
//         递归左孩子
        root.right = pruneLeaves(root.right);
//         递归右孩子
        return root;
    }
}

时空复杂度

时间复杂度： $O(n)O(n)$

理由如下：我们可以发现这么一个问题，我们在遍历整个树的时候，我们每一个点只会进去一次，然后出去一次，所以最后我们是走了$2\ast n2\; *\; n$个点，时间复杂度不带常数，所以最后的时间复杂度就是$O(n)O(n)$

空间复杂度： $O(n)O(n)$

理由如下：因为使用的二叉树深度的一个递归栈，根据二叉树的性质，一般情况下，我们的深度是$O(logn)O(logn)$，但是在极限的情况下，我们的树退化成为了一条链，那么我们的深度就是$O(n)O(n)$，所以我们的空间复杂度应该是$O(n)O(n)$