线性代数之——消元法

1. 消元的思想

针对下面的方程，我们无法直接得到方程的解。

$\begin{array}{cccc}{\displaystyle }& {\displaystyle x-}& {\displaystyle 2}& {\displaystyle y=1}\\ {\displaystyle 3}& {\displaystyle x+}& {\displaystyle 2}& {\displaystyle y=11}\end{array}$3​x − x + ​22​y = 1y = 11​

但如果我们将第二个方程减去第一个方程的 3 倍，上面的方程组就变成了下面这样。

$\begin{array}{cccc}{\displaystyle }& {\displaystyle x-}& {\displaystyle 2}& {\displaystyle y=1}\\ {\displaystyle }& {\displaystyle }& {\displaystyle 8}& {\displaystyle y=8}\end{array}$​x −   ​28​y = 1y = 8​

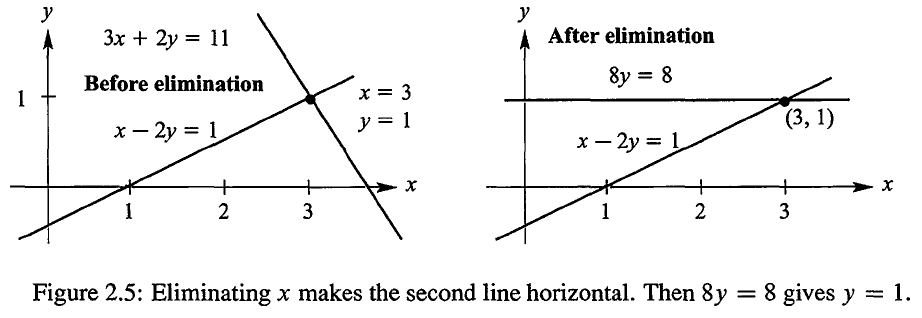
这时候，我们就可以直接得到 $y=1$y=1，进而从第一个方程得到 $x=3$x=3。

可以看到，消元之后，方程组变成了一个下三角(upper triangular)的形式，然后我们就可以用回带法(back substitution)来快速地解出方程组的解。

进行消元的那一行的第一个非零值称为主元（pivot），消元时候的乘数就等于待消项的系数除以主元，在上面的例子中，乘数 $3=3/1$3=3/1。一般地，乘数可以表示为
$l_{ij}=\frac{第i行待消去项的系数}{第j行的主元}$lij​=第 j 行的主元第 i 行待消去项的系数​

$\begin{array}{cccc}{\displaystyle 4}& {\displaystyle x-}& {\displaystyle 8}& {\displaystyle y=4}\\ {\displaystyle 3}& {\displaystyle x+}& {\displaystyle 2}& {\displaystyle y=11}\end{array}$43​x − x + ​82​y = 4y = 11​

如果我们改变了第一个方程，那么乘数就等于 $3/4$3/4。消元之后，所有的主元都位于下三角的对角线上，并且主元不能是 0。

$\begin{array}{cccc}{\displaystyle 4}& {\displaystyle x-}& {\displaystyle 8}& {\displaystyle y=4}\\ {\displaystyle }& {\displaystyle }& {\displaystyle 8}& {\displaystyle y=8}\end{array}$4​x −   ​88​y = 4y = 8​

2. 消元的失效

• 无解
  $\begin{array}{cccc}{\displaystyle }& {\displaystyle x-}& {\displaystyle 2}& {\displaystyle y=1}\\ {\displaystyle 3}& {\displaystyle x-}& {\displaystyle 6}& {\displaystyle y=11}\end{array}消元后\begin{array}{cccc}{\displaystyle }& {\displaystyle x-}& {\displaystyle 2}& {\displaystyle y=1}\\ {\displaystyle }& {\displaystyle }& {\displaystyle 0}& {\displaystyle y=8}\end{array}$3​x − x − ​26​y = 1y = 11​消元后​x −   ​20​y = 1y = 8​

这种情况下，我们遇到了 $0y=8$0y=8，说明原方程组无解。从行图像中，我们也可以看到，两条平行的直线无法相交于一点。而在列图像中，两个在同一方向上的向量不可能线性组合出不在这个方向上的向量。

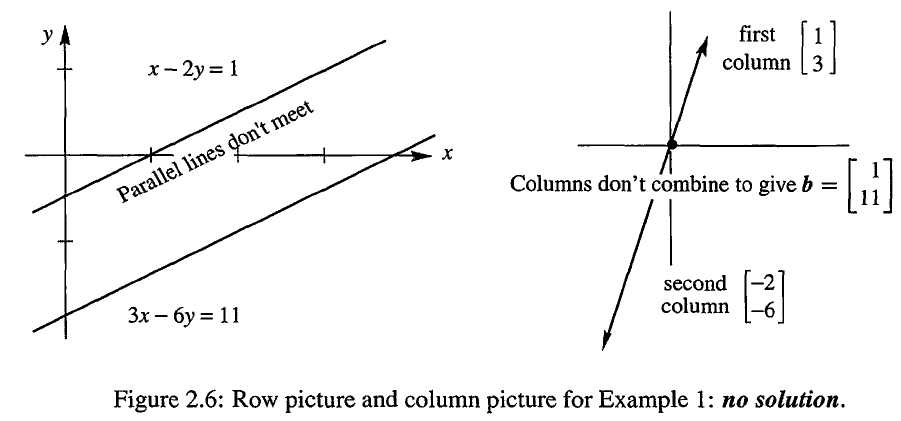
• 无穷解
  $\begin{array}{cccc}{\displaystyle }& {\displaystyle x-}& {\displaystyle 2}& {\displaystyle y=1}\\ {\displaystyle 3}& {\displaystyle x-}& {\displaystyle 6}& {\displaystyle y=3}\end{array}消元后\begin{array}{cccc}{\displaystyle }& {\displaystyle x-}& {\displaystyle 2}& {\displaystyle y=1}\\ {\displaystyle }& {\displaystyle }& {\displaystyle 0}& {\displaystyle y=0}\end{array}$3​x − x − ​26​y = 1y = 3​消元后​x −   ​20​y = 1y = 0​

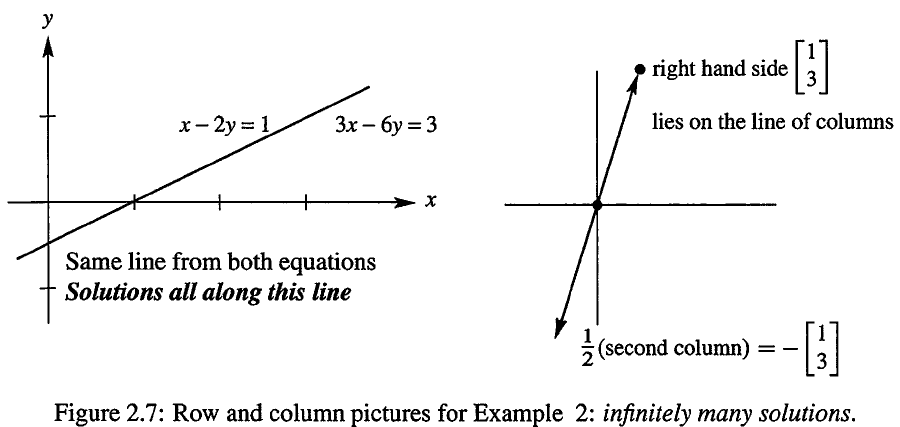
这种情况下，我们遇到了 $0y=0$0y=0，任何的 $y$y 值都满足要求，此时 $y$y 是“自由”的，确定了 $y$y 之后 $x$x 则由第一个方程确定。

从行图像中，我们也可以看到，两条直线相同，因此整条直线都是交点。而在列图像中，左边的两个向量和右边的向量方向都相同，有无穷多个线性组合都可以产生右边的向量。

对于有 $n$n 个方程的方程组，如果我们得不到 $n$n 个主元，那么消元就会导致 $0̸=0，无解$0̸​=0，无解 或者 $0=0，无穷解$0=0，无穷解 ，只有正好有 $n$n 个主元的时候，方程组才有解，但我们可能需要进行方程的交换。

• 需要行交换

$\begin{array}{cccc}{\displaystyle 0}& {\displaystyle x+}& {\displaystyle 2}& {\displaystyle y=4}\\ {\displaystyle 3}& {\displaystyle x-}& {\displaystyle 2}& {\displaystyle y=5}\end{array}消元后\begin{array}{cccc}{\displaystyle 3}& {\displaystyle x-}& {\displaystyle 2}& {\displaystyle y=5}\\ {\displaystyle }& {\displaystyle }& {\displaystyle 2}& {\displaystyle y=4}\end{array}$03​x + x − ​22​y = 4y = 5​消元后3​x −   ​22​y = 5y = 4​

一开始，第一行的主元为 0，行交换后，我们得到了两个主元 3 和 2，然后，方程就有了正常的解。

3. 三个未知数

$\begin{array}{cccccc}{\displaystyle 2}& {\displaystyle x+}& {\displaystyle 4}& {\displaystyle y-}& {\displaystyle 2}& {\displaystyle z=2}\\ {\displaystyle 4}& {\displaystyle x+}& {\displaystyle 9}& {\displaystyle y-}& {\displaystyle 3}& {\displaystyle z=8}\\ {\displaystyle -2}& {\displaystyle x-}& {\displaystyle 3}& {\displaystyle y+}& {\displaystyle 7}& {\displaystyle z=10}\end{array}$24−2​x + x + x − ​493​y − y − y + ​237​z= 2z= 8z= 10​

第一步，方程 2 减去 2 倍的方程 1，得到 $y+z=4$y+z=4。
第二步，方程 3 减去 -1 倍的方程 1，得到 $y+5z=12$y+5z=12。
第一步，方程 3 减去 1 倍的方程 2，得到 $4z=8$4z=8。

$\begin{array}{cccccc}{\displaystyle 2}& {\displaystyle x+}& {\displaystyle 4}& {\displaystyle y-}& {\displaystyle 2}& {\displaystyle z=2}\\ {\displaystyle }& {\displaystyle }& {\displaystyle 1}& {\displaystyle y+}& {\displaystyle 1}& {\displaystyle z=8}\\ {\displaystyle }& {\displaystyle }& {\displaystyle }& {\displaystyle }& {\displaystyle 4}& {\displaystyle z=8}\end{array}$2​x +     ​41​y − y +   ​214​z= 2z= 8z= 8​

三个主元分别为 2， 1， 4，然后我们就可以用回带法求出方程组的解。

4. 用矩阵的形式来消元

$\begin{array}{cccccc}{\displaystyle 2}& {\displaystyle x_1+}& {\displaystyle 4}& {\displaystyle x_2-}& {\displaystyle 2}& {\displaystyle x_3=2}\\ {\displaystyle 4}& {\displaystyle x_1+}& {\displaystyle 9}& {\displaystyle x_2-}& {\displaystyle 3}& {\displaystyle x_3=8}\\ {\displaystyle -2}& {\displaystyle x_1-}& {\displaystyle 3}& {\displaystyle x_2+}& {\displaystyle 7}& {\displaystyle x_3=10}\end{array}\leftrightarrow \left[\begin{array}{ccc}2& 4& -2\\ 4& 9& -3\\ -2& -3& 7\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right]=\left[\begin{array}{c}2\\ 8\\ 10\end{array}\right]$24−2​x1​ + x1​ + x1​ − ​493​x2​ − x2​ − x2​ + ​237​x3​= 2x3​= 8x3​= 10​↔⎣⎡​24−2​49−3​−2−37​⎦⎤​⎣⎡​x1​x2​x3​​⎦⎤​=⎣⎡​2810​⎦⎤​

对方程的两边同时进行一步消元，第 2 个方程减去第 1 个方程的 2 倍，我们可以得到：

$\left[\begin{array}{ccc}2& 4& -2\\ 0& 1& 1\\ -2& -3& 7\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right]=\left[\begin{array}{c}2\\ 4\\ 10\end{array}\right]$⎣⎡​20−2​41−3​−217​⎦⎤​⎣⎡​x1​x2​x3​​⎦⎤​=⎣⎡​2410​⎦⎤​

相当于左右两边都乘以了一个矩阵 $E_{21}$E21​

$E_{21}=\left[\begin{array}{ccc}1& 0& 0\\ -2& 1& 0\\ 0& 0& 1\end{array}\right]$E21​=⎣⎡​1−20​010​001​⎦⎤​

$E_{21}=\left[\begin{array}{ccc}1& 0& 0\\ -2& 1& 0\\ 0& 0& 1\end{array}\right]\ast \left[\begin{array}{c}row1\\ row2\\ row3\end{array}\right]=\left[\begin{array}{c}row1\\ row2-2row1\\ row3\end{array}\right]$E21​=⎣⎡​1−20​010​001​⎦⎤​∗⎣⎡​row1row2row3​⎦⎤​=⎣⎡​row1row2−2row1row3​⎦⎤​

$E_{21}$E21​ 称为初等矩阵（elementary matrix）或者消元矩阵（elimination matrix），它可以很简单地从单位矩阵演化而来， $E_{ij}$Eij​ 就是将单位矩阵 $(i,j)$(i,j) 位置的 0 换成消元过程的乘数 $-l_{ij}$−lij​。

$I=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]\to E_{21}=\left[\begin{array}{ccc}1& 0& 0\\ \boxed{{\displaystyle -2}}& 1& 0\\ 0& 0& 1\end{array}\right]$I=⎣⎡​100​010​001​⎦⎤​→E21​=⎣⎡​1−2​0​010​001​⎦⎤​

获取更多精彩，请关注「seniusen」!