题干:
A plane is flying at a constant height of hh meters above the ground surface. Let's consider that it is flying from the point (−109,h)(−109,h) to the point (109,h)(109,h) parallel with OxOx axis.
A glider is inside the plane, ready to start his flight at any moment (for the sake of simplicity let's consider that he may start only when the plane's coordinates are integers). After jumping from the plane, he will fly in the same direction as the plane, parallel to OxOx axis, covering a unit of distance every second. Naturally, he will also descend; thus his second coordinate will decrease by one unit every second.
There are ascending air flows on certain segments, each such segment is characterized by two numbers x1x1 and x2x2 (x1<x2x1<x2) representing its endpoints. No two segments share any common points. When the glider is inside one of such segments, he doesn't descend, so his second coordinate stays the same each second. The glider still flies along OxOx axis, covering one unit of distance every second.
If the glider jumps out at 11, he will stop at 1010. Otherwise, if he jumps out at 22, he will stop at 1212.
Determine the maximum distance along OxOx axis from the point where the glider's flight starts to the point where his flight ends if the glider can choose any integer coordinate to jump from the plane and start his flight. After touching the ground the glider stops altogether, so he cannot glide through an ascending airflow segment if his second coordinate is 00.
Input
The first line contains two integers nn and hh (1≤n≤2⋅105,1≤h≤109)(1≤n≤2⋅105,1≤h≤109) — the number of ascending air flow segments and the altitude at which the plane is flying, respectively.
Each of the next nn lines contains two integers xi1xi1 and xi2xi2 (1≤xi1<xi2≤109)(1≤xi1<xi2≤109) — the endpoints of the ii-th ascending air flow segment. No two segments intersect, and they are given in ascending order.
Output
Print one integer — the maximum distance along OxOx axis that the glider can fly from the point where he jumps off the plane to the point where he lands if he can start his flight at any integer coordinate.
Examples
Input
3 4 2 5 7 9 10 11
Output
10
Input
5 10 5 7 11 12 16 20 25 26 30 33
Output
18
Input
1 1000000000 1 1000000000
Output
1999999999
Note
In the first example if the glider can jump out at (2,4)(2,4), then the landing point is (12,0)(12,0), so the distance is 12−2=1012−2=10.
In the second example the glider can fly from (16,10)(16,10) to (34,0)(34,0), and the distance is 34−16=1834−16=18.
In the third example the glider can fly from (−100,1000000000)(−100,1000000000) to (1999999899,0)(1999999899,0), so the distance is 1999999899−(−100)=19999999991999999899−(−100)=1999999999.
题目大意:
你现在处于高度为h的地方,每秒y坐标会减少1,x坐标会增加1,而现在会有n个气流区[l,r],在每个气流区中,你的y坐标不会改变,你的x坐标每秒会增加1。(保证所给出的气流两两之间没有交集)现在你可以从x轴上的任意一点下落,现在问你最远的飞行路径。(即终点x坐标 减 起点x坐标的最大值)
解题报告:
大体:看到数据量,nlogn解决,于是乎枚举每一个起点,二分找到终点,维护最大值,就可以了呀。
仔细分析:
首先要分析出,把竖直下落的高度转换成走过的间隙的长度和(高中物理题貌似这种转化套路很多见?)然后我们看在这些个间隙下,能走多长个气流(不是越多越好,而是越长越好),维护一个maxx,然后最后答案就是maxx + h就可以了。
不明白可以看下面的图:
可以看成是这个东西:
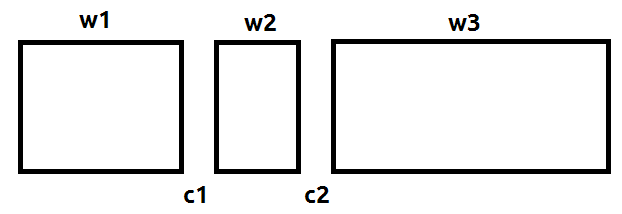
相当于是在选取的ci≤h的情况下,使Σwi最大。
AC代码:
#include<bits/stdc++.h>
using namespace std;
const int MAX = 2e5 + 5;
int n,h;
int b[MAX],c[MAX];
struct Node {
int l,r;
} node[MAX];
int main()
{
cin>>n>>h;
for(int i = 1; i<=n; i++) scanf("%d%d",&node[i].l,&node[i].r);
c[1] = 0;b[1] = node[1].r-node[1].l;
for(int i = 2; i<=n; i++) {
b[i] = node[i].r - node[i].l;
c[i] = node[i].l - node[i-1].r;
b[i] += b[i-1];
c[i] += c[i-1];
}
c[n+1] = INT_MAX;//这句貌似可以没有、、
int maxx = -1,ans;
for(int i = 1; i<=n; i++) {
int pos = lower_bound(c+1,c+n+1,c[i]+h) - c;
ans = b[pos-1] - b[i-1];
maxx = max(maxx,ans);
}
printf("%d\n",maxx+h);
return 0 ;
}
/*
2 3
1 2
3 4
*/ 总结:
就是要多逼着自己做做D题啊!!!有的时候也不算很难想,不是高不可攀,是不是?
关于初始化:这里对于i=1的情况单独做了初始化,然后从i=2开始进入for循环,是正解,但是不加初始化,直接i=1开始计入for,也可以ac,但是就说不太过去,反正输出c[2]的值是和我们想得到的值是不一样的,换句话说,是不合法的。
记住一个套路:
求前缀和 + 二分。其中二分寻值时可以依附于正在枚举的i上,就像这个题,二分找的就是c[i]相关的。这样就避免了很麻烦的双指针:链接在此
#include <bits/stdc++.h>
#define maxn 200005
using namespace std;
struct Node{
int l,r;
}q[maxn];
typedef long long ll;
int main()
{
ll n,h;
cin>>n>>h;
for(int i=0;i<n;i++){
scanf("%I64d%I64d",&q[i].l,&q[i].r);
}
ll l,r,tmp1,tmp2;
l=q[0].l,r=q[0].r+h;//首先l指针先指向第一个气流的起点,r指针指向落点
ll ans=h;
tmp1=tmp2=0;
while(tmp1<n){//枚举每一个气流
while(tmp2+1<n&&q[tmp2+1].l<r){
//如果下一个气流的左区间在终点前,则证明出现情况2,则将终点加上该气流的区间大小
tmp2++;
r+=q[tmp2].r-q[tmp2].l;
}
ans=max(ans,r-l);//记录r-l的最大值
tmp1++;
l=q[tmp1].l;//将起点置为下一个气流的起点
r+=q[tmp1].l-q[tmp1-1].r; //加上气流与气流之间的大小
}
cout<<ans<<endl;
}
或者一位红名大佬的双指针:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
#define mp make_pair
const int N = 200200;
int n, h;
int a[N][2];
int ans;
int main()
{
scanf("%d%d", &n, &h);
for (int i = 0; i < n; i++) scanf("%d%d", &a[i][0], &a[i][1]);
int r = 0;
int curH = h;
for (int l = 0; l < n; l++) {
while(r < n - 1 && curH > a[r + 1][0] - a[r][1]) {
curH -= a[r + 1][0] - a[r][1];
r++;
}
ans = max(ans, a[r][1] - a[l][0] + curH);
if (l < n - 1)
curH += a[l + 1][0] - a[l][1];
}
printf("%d\n", ans);
return 0;
} 或者app大佬:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 200000;
int n, h, l[maxn + 10], r[maxn + 10], m;
pair<ll, ll> a[maxn + 10];
int idl = 1, idr = 1;
ll lenl = -1e18, lenr = -1e18, ans;
int main() {
scanf("%d%d", &n, &h);
lenr += h; ans = h;
for (int i = 1; i <= n; ++i) scanf("%d%d", &l[i], &r[i]);
a[++m] = make_pair(-(long long)1e18, l[1]);
for (int i = 2; i <= n; ++i)
a[++m] = make_pair(r[i - 1], l[i]);
a[++m] = make_pair(r[n], (long long)1e18);
while (idl <= m && idr <= m) {
ans = max(ans, lenr - lenl);
ll dist = min(a[idr].second - lenr, a[idl].second - lenl);
lenl += dist; lenr += dist;
if (lenl < a[idl].second) ++lenl;
else lenl = a[++idl].first + 1;
if (lenr < a[idr].second) ++lenr;
else lenr = a[++idr].first + 1;
}
printf("%lld", ans);
}




 京公网安备 11010502036488号
京公网安备 11010502036488号