今日小结：今天上午熟练了一下前面复习的内容，下午复习了并查集和拓扑排序，整体还算可以，但是并查集思路有点难想，然后晚上听了lyk讲题，整理了博客。明天的任务是最小环和差分约束。

一. 今日完成的题目：

洛谷SP14932，CF519E，洛谷P2812，洛谷P3003，洛谷P1967，洛谷P2342，洛谷P1197

二.

1. 当天完成题目数：7道。

2. 未完成6个题目的原因：

3. 复习的知识点：tarjan，最短路，LCA，拓扑排序，并查集

4.不会题目：无

三：

1. 洛谷 SP14932 LCA - Lowest Common Ancestor

Description:

一棵树是一个简单无向图，图中任意两个节点仅被一条边连接，所有连通无环无向图都是一棵树。\(-Wikipedia\)

最近公共祖先（\(LCA\)）是……（此处省去对\(LCA\)的描述），你的任务是对一棵给定的树\(T\)以及上面的两个节点\(u,v\)求出他们的\(LCA\)。

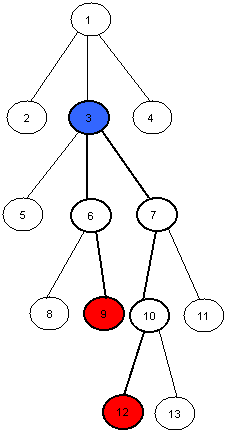
例如图中9和12号节点的LCA为3号节点

Input:

输入的第一行为数据组数\(T\)，对于每组数据，第一行为一个整数\(N(1\leq N\leq1000)\)，节点编号从\(1\)到\(N\)，接下来的\(N\)行里每一行开头有一个数字\(M(0\leq M\leq999)\)，\(M\)为第\(i\)个节点的子节点数量，接下来有\(M\)个数表示第\(i\)个节点的子节点编号。下面一行会有一个整数\(Q(1\leq Q\leq1000)\)，接下来的\(Q\)行每行有两个数\(u,v\)，输出节点\(u,v\)在给定树中的\(LCA\)。

输入数据保证只有一个根节点并且没有环。

Output:

对于每一组数据输出\(Q+1\)行，第一行格式为\("Case i:"\)（没有双引号），\(i\)表示当前数据是第几组，接下来的\(Q\)行每一行一个整数表示一对节点\(u,v\)的\(LCA\)。

Sample Input:

1
7
3 2 3 4
0
3 5 6 7
0
0
0
0
2
5 7
2 7

Sample Output:

Case 1:
3
1

\(Translated by @_yxl_g\)l_

思路：一道求\(LCA\)的板子题，根据题目给出的每个点的孩子建边然后找出根结点，直接\(dfs\)求出深度后跑\(LCA\)就可以了。

代码：

#include<cstdio>
#include<algorithm>
#include<cstring>
#define maxn 1007
using namespace std;
int t,q,rt,tim,f[maxn][22],n,m,head[maxn],d[maxn],num;
bool vis[maxn];
struct node {
  int v,nxt;
}e[maxn<<1];
inline void ct(int u, int v) {
  e[++num].v=v;
  e[num].nxt=head[u];
  head[u]=num;
}
void dfs(int u, int fa) {
  for(int i=head[u];i;i=e[i].nxt) {
    int v=e[i].v;
    if(v!=fa) {
      f[v][0]=u;
      d[v]=d[u]+1;
      dfs(v,u);
    }
  }
}
inline int lca(int a, int b) {
  if(d[a]>d[b]) swap(a,b);
  for(int i=20;i>=0;--i) 
  if(d[a]<=d[b]-(1<<i)) b=f[b][i];
  if(a==b) return a;
  for(int i=20;i>=0;--i)
  if(f[a][i]!=f[b][i]) a=f[a][i],b=f[b][i];
  return f[a][0];
}
int main() {
  scanf("%d",&t);
  while(t--) {
    ++tim;
    memset(f,0,sizeof(f));
    memset(d,0,sizeof(d));
    memset(head,0,sizeof(head));
    memset(vis,0,sizeof(vis));
    num=0;
    scanf("%d",&n);
    for(int i=1,m;i<=n;++i) {
      scanf("%d",&m);
      for(int j=1,v;j<=m;++j) {
        scanf("%d",&v);
        ct(i,v);ct(v,i);
        vis[v]=1;
      }
    }
    for(int i=1;i<=n;++i) if(!vis[i]) rt=i;
    dfs(rt,0);
    for(int j=1;j<=20;++j)
    for(int i=1;i<=n;++i)
    f[i][j]=f[f[i][j-1]][j-1];
    scanf("%d",&q);
    printf("Case %d:\n",tim);
    for(int i=1,u,v;i<=q;++i) {
      scanf("%d%d",&u,&v);
      printf("%d\n",lca(u,v));
    }
  }
  return 0;
}

2. CF519E A and B and Lecture Rooms

题目描述

\(A\)和\(B\)在准备参加编程比赛。

\(A\)和\(B\)学习的大学的房间由走廊连接。大学一共有nn 个房间，由\(n-1\)条走廊连接，房间的编号是从\(1\)到\(n\)的数字编号。

\(A\)和\(B\)在大学的某些房间里进行比赛。在每场比赛之后，他们会一起在一个房间里讨论问题。\(A\)和\(B\)希望这个讨论问题的房间到分别他们两个人比赛房间的距离相等。两个房间之间的距离指他们之间最短路的边数。

因为\(A\)和\(B\)每天都在不一样的房间里比赛，所以他们请求你告诉他们在接下来比赛的\(m\) 天里可以用来讨论问题的房间有多少个？

输入输出格式

输入格式

第一行包括整数\(n\)，其中\((1 \leq n \leq 10^5)\)，表示房间数量。

接下来的\(n-1\)行描述所有的走廊。这\(n-1\)行中的第\(i\)行包括两个整数\(a_i\)和\(b_i\)，表示第ii 条走廊连接了房间\(a_i\)和\(b_i\)。

接下来的一行输入比赛的天数\(m(1 \leq m \leq 10^5)\)。

再接下来的\(m\)行，第\(j\)行包含两个整数\(x_j\)和\(y_j(1 \leq x_j,y_j \leq n)\)，表示比赛的第\(j\)天\(A\)将在\(x_j\)房间比赛，\(B\)将在\(y_j\)房间比赛。

输出格式

在第\(i(1 \leq i \leq m)\)行输出当天分别到\(A\)、\(B\)比赛的房间距离相等的房间数量。

输入输出样例

输入样例#1：

4
1 2
1 3
2 4
1
2 3

输出样例#1：

1

输入样例#2：

4
1 2
2 3
2 4
2
1 2
1 3

输出样例#2：

0
2

思路：这道题……是道好题，题意是给你一棵树，对于每次询问，每个询问给出两个点，让你求有几个点到这两个点的距离是相等的，首先，每条边的边权是\(1\)，因此每个点的深度就是它到根结点的距离，然后通过样例和自己手玩发现，如果它们到它们的\(LCA\)的距离之和是奇数，那么答案必然是\(0\)，其次如果两个点深度是相同的，那么答案就是以它们以根结点为根的树的点的个数(即\(n\))减去以这两个点为根的子树的点的个数，还有一种情况，那就是深度不相同，则找一个这两点之间的中间结点，然后答案就是以这个中间结点为根的子树点的个数减去以这以两点深度较深的点为根的子树点的个数。求中间结点可以用类似求\(LCA\)中\(f\)数组的方法来求。就是让较深的结点向上跳这两点距离的二分之一。

代码：

#include<cstdio>
#include<algorithm>
#include<cctype>
#define maxn 100007
using namespace std;
int n,t,head[maxn],d[maxn],num,f[maxn][22],size[maxn];
inline int qread() {
  char c=getchar();int num=0,f=1;
  for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
  for(;isdigit(c);c=getchar()) num=num*10+c-'0';
  return num*f;
}
struct node {
  int v,nxt;
}e[maxn<<1];
inline void ct(int u, int v) {
  e[++num].v=v;
  e[num].nxt=head[u];
  head[u]=num;
}
void dfs(int u, int fa) {
  for(int i=head[u];i;i=e[i].nxt) {
    int v=e[i].v;
    if(v!=fa) {
      f[v][0]=u;
      d[v]=d[u]+1;
      dfs(v,u);
      size[u]+=size[v];
    }
  }
}
inline int lca(int a, int b) {
  if(d[a]>d[b]) swap(a,b);
  for(int i=20;i>=0;--i)
  if(d[a]<=d[b]-(1<<i)) b=f[b][i];
  if(a==b) return a;
  for(int i=20;i>=0;--i)
  if(f[a][i]!=f[b][i]) a=f[a][i],b=f[b][i];
  return f[a][0];
}
int main() {
  n=qread();
  for(int i=1,u,v;i<n;++i) {
    u=qread(),v=qread();
    ct(u,v);ct(v,u);
  }
  for(int i=1;i<=n;++i) size[i]=1;
  dfs(1,0);
  for(int j=1;j<=20;++j)
  for(int i=1;i<=n;++i)
  f[i][j]=f[f[i][j-1]][j-1];
  t=qread();
  for(int i=1,u,v;i<=t;++i) {
    u=qread(),v=qread();
    if(d[u]<d[v]) swap(u,v);
    if((d[u]+d[v]-2*(lca(u,v)))&1) {printf("0\n");continue;}
    int lc=lca(u,v),x=u; 
    int p=(d[u]+d[v]-2*d[lc])/2-1;
    for(int i=20;i>=0;--i) if(p&(1<<i)) u=f[u][i];
    if(d[x]==d[v]) {
      p=d[v]-d[lc]-1;
      for(int i=20;i>=0;--i) if(p&(1<<i)) v=f[v][i];
      printf("%d\n",n-size[u]-size[v]);
    }
    else printf("%d\n",size[f[u][0]]-size[u]);
  }
  return 0;
}

3. 洛谷P2812校园网络【Network of Schools加强版】

题目背景

浙江省的几所\(OI\)强校的神犇发明了一种人工智能，可以\(AC\)任何题目，所以他们决定建立一个网络来共享这个软件。但是由于他们脑力劳动过多导致全身无力身体被\(♂\)掏\(♂\)空，他们来找你帮助他们。

题目描述

共有\(n\)所学校\(（n \leq 10000）\)已知他们实现设计好的网络共\(m\)条线路，为了保证高速，网络是单向的。现在请你告诉他们至少选几所学校作为共享软件的母机母鸡，能使每所学校都可以用上。再告诉他们至少要添加几条线路能使任意一所学校作为母机母鸡都可以使别的学校使用上软件。

输入输出格式

输入格式：

第一行一个整数\(n\)。

接下来\(n\)行每行有若干个整数，用空格空格隔开。

第\(i-1\)行的非零整数\(x\)，表示从\(i\)到\(x\)有一条线路。以\(0\)作为结束标志。

输出格式：

第一行一个整数表示问题1的答案。

第二行回答问题2.

输入输出样例

输入样例#1：

5
2 0
4 0
5 0
1 0
0

输出样例#1：

2
2

说明

\(POJ\)原题。数据扩大了\(100\)倍。

\(边数 \leq 5000000 ≤ 5000000\)

思路：这道题是洛谷\(P2746\)的数据加强版，但是……还是没法卡掉\(tarjan\)做法啊，毕竟正解就是\(tarjan\)，直接把洛谷\(P2746\)的代码粘过来然后把数组改大些就可以了……

代码：

#include<cstdio>
#include<iostream>
#include<stack>
#define maxn 10007
using namespace std;
int n,num,js,cnt,rd[maxn],cd[maxn],head[maxn],dfn[maxn],low[maxn],bel[maxn],size[maxn];
int x1,x2;
bool vis[maxn];
struct node {
  int v,nxt;
}e[5000007];
inline void ct(int u, int v) {
  e[++num].v=v;
  e[num].nxt=head[u];
  head[u]=num;
}
inline int maxx(int a, int b) {return a>=b?a:b;}
stack<int>q;
void tarjan(int u) {
  dfn[u]=low[u]=++cnt;
  q.push(u),vis[u]=1;
  for(int i=head[u];i;i=e[i].nxt) {
    int v=e[i].v;
    if(!dfn[v]) tarjan(v),low[u]=min(low[u],low[v]);
    else if(vis[v]) low[u]=min(low[u],dfn[v]);
  }
  if(dfn[u]==low[u]) {
    int x=-1;js++;
    while(x!=u) {
      x=q.top(),q.pop();
      bel[x]=js,size[js]++;
      vis[x]=0;
    }
  }
}
int main() {
  scanf("%d",&n);
  for(int i=1,x;i<=n;++i) {
    while(scanf("%d",&x)==1) {
      if(!x) break;
      ct(i,x);
    }
  }
  for(int i=1;i<=n;++i) if(!dfn[i]) tarjan(i);
  if(js==1) {printf("1\n0\n");return 0;};
  for(int k=1;k<=n;++k) {
    for(int i=head[k];i;i=e[i].nxt) {
      int v=e[i].v;
      if(bel[k]!=bel[v]) ++cd[bel[k]],++rd[bel[v]];
    }
  }
  for(int i=1;i<=js;++i) {
    if(!cd[i]) ++x1;
    if(!rd[i]) ++x2;
  }
  printf("%d\n%d\n",x2,max(x1,x2));
  return 0;
}

4. 洛谷P3003 苹果交货Apple Delivery

题目描述

贝西有两个又香又脆的红苹果要送给她的两个朋友。当然她可以走的\(C（1 \leq C \leq 200000）\)条“牛路”都被包含在一种常用的图中，包含了\(P（1 \leq P \leq 100000）\)个牧场，分别被标为\(1..P\)。没有“牛路”会从一个牧场又走回它自己。“牛路”是双向的，每条牛路都会被标上一个距离。最重要的是，每个牧场都可以通向另一个牧场。每条牛路都连接着两个不同的牧场\(P1_i\)和\(P2_i（1<=P1_i,p2_i<=P)\)，距离为\(D_i\)。所有“牛路”的距离之和不大于\(2000000000\)。

现在，贝西要从牧场\(PB\)开始给\(PA_1\)和\(PA_2\)牧场各送一个苹果（\(PA_1\)和\(PA_2\)顺序可以调换），那么最短的距离是多少呢？当然，\(PB、PA_1\)和\(PA_2\)各不相同。

输入输出格式

输入格式：

• Line \(1\): Line \(1\) contains five space-separated integers: \(C, P, PB, PA_1\), and \(PA_2\)

• Lines \(2..C+1\): Line \(i+1\) describes cowpath i by naming two pastures it connects and the distance between them: \(P1_i, P2_i, D_i\)

输出格式：

• Line 1: The shortest distance Bessie must travel to deliver both apples

输入输出样例

输入样例#1：

9 7 5 1 4 
5 1 7 
6 7 2 
4 7 2 
5 6 1 
5 2 4 
4 3 2 
1 2 3 
3 2 2 
2 6 3 

输出样例#1：

12

思路：一道裸的最短路题目，跟其他最短路题目不一样的是，这道题目要求的是起点到两个点的最短路之和，且这两个点可以调换，那么我们可以考虑以这两个点分别为起点，求到\(PB\)的最短路和到另一个点的最短路，然后取最小值。跑最短路用堆优化\(dijkstra\)即可。

代码：

#include<cstdio>
#include<algorithm>
#include<cctype>
#include<queue>
#include<cstring>
#define maxn 100007
using namespace std;
int n,m,num,head[maxn],s,a,b,dis[maxn];
inline int qread() {
  char c=getchar();int num=0,f=1;
  for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
  for(;isdigit(c);c=getchar()) num=num*10+c-'0';
  return num*f;
}
struct Edge {
  int v,w,nxt;
}e[maxn<<2];
struct node {
  int x,y;
  bool operator < (const node &a) const{return y>a.y;}
};
inline void ct(int u, int v, int w) {
  e[++num].v=v;
  e[num].w=w;
  e[num].nxt=head[u];
  head[u]=num;
}
priority_queue<node>q;
inline void dijkstra(int s) {
  memset(dis,0x3f,sizeof(dis));
  q.push((node){s,0}),dis[s]=0;
  while(!q.empty()) {
    int u=q.top().x,d=q.top().y;
    q.pop();
    if(d!=dis[u]) continue;
    for(int i=head[u];i;i=e[i].nxt) {
      int v=e[i].v;
      if(dis[v]>dis[u]+e[i].w) {
        dis[v]=dis[u]+e[i].w;
        q.push((node){v,dis[v]});
      }
    }
  }
}
int main() {
  m=qread(),n=qread(),s=qread(),a=qread(),b=qread();
  for(int i=1,u,v,w;i<=m;++i) {
    u=qread(),v=qread(),w=qread();
    ct(u,v,w);ct(v,u,w);
  }
  dijkstra(a);
  int zrj=dis[s]+dis[b];
  dijkstra(b);
  int cyh=dis[s]+dis[a];
  printf("%d\n",min(cyh,zrj));
  return 0;
}

5. 洛谷P1967 货车运输

题目描述

\(A\)国有\(n\)座城市，编号从\(1\)到\(n\)，城市之间有\(m\)条双向道路。每一条道路对车辆都有重量限制，简称限重。现在有\(q\)辆货车在运输货物， 司机们想知道每辆车在不超过车辆限重的情况下，最多能运多重的货物。

输入输出格式

输入格式：

第一行有两个用一个空格隔开的整数\(n,m\)表示\(A\)国有\(n\)座城市和\(m\)条道路。

接下来\(m\)行每行\(3\)个整数\(x, y, z\)，每两个整数之间用一个空格隔开，表示从\(x\)号城市到\(y\)号城市有一条限重为\(z\)的道路。注意： x不等于y，两座城市之间可能有多条道路 。

接下来一行有一个整数\(q\)，表示有\(q\)辆货车需要运货。

接下来\(q\)行，每行两个整数\(x、y\)，之间用一个空格隔开，表示一辆货车需要从 \(x\) 城市运输货物到 \(y\) 城市，注意： x 不等于 y 。

输出格式：

共有\(q\)行，每行一个整数，表示对于每一辆货车，它的最大载重是多少。如果货车不能到达目的地，输出\(-1\)。

输入输出样例

输入样例#1：

4 3
1 2 4
2 3 3
3 1 1
3
1 3
1 4
1 3

输出样例#1：

3
-1
3

说明

对于\(30\%\)的数据，\(0 < n < 1,000,0 < m < 10,000,0 < q< 1,000\)；
对于60%的数据，0 < n < 1,000,0 < m < 50,000,0 < q< 1,000；

对于100%的数据，\(0 < n < 10,000,0 < m < 50,000,0 < q< 30,000,0 ≤ z ≤ 100,000\).

思路：想出来最大生成树+LCA这道题就基本没什么问题了，就是先跑一遍最大生产树，然后建边，之后在求LCA的过程中记录最小值，然后val数组跟f数组一起更新。然后就完了……

代码：

#include<cstdio>
#include<algorithm>
#define maxn 10007
using namespace std;
int head[maxn],n,m,fa[maxn],f[maxn][22],p,x,y,num,d[maxn],val[maxn][22];
bool vis[maxn];
struct node {
  int v,w,nxt;
}e[100007];
struct Edge {
  int u,v,w;
}a[100007];
inline void ct(int u, int v, int w) {
  e[++num].v=v;
  e[num].w=w;
  e[num].nxt=head[u];
  head[u]=num;
}
inline int find(int x) {return fa[x]==x?x:fa[x]=find(fa[x]);}
inline bool cmp(Edge a,Edge b) {return a.w>b.w;}
void dfs(int u) {
  vis[u]=1;
  for(int i=head[u];i;i=e[i].nxt) {
    int v=e[i].v;
    if(!vis[v]) {
      d[v]=d[u]+1;
      f[v][0]=u;
      val[v][0]=e[i].w;
      dfs(v);
    }
  }
}
inline int lca(int a, int b) {
  if(find(a)!=find(b)) return -1;
  int ans=1020040222;
  if(d[a]>d[b]) swap(a,b);
  for(int i=20;i>=0;--i)
  if(d[a]<=d[b]-(1<<i)) ans=min(ans,val[b][i]),b=f[b][i];
  if(a==b) return ans;
  for(int i=20;i>=0;--i)
  if(f[a][i]!=f[b][i]) {
    ans=min(ans,min(val[a][i],val[b][i]));
    a=f[a][i],b=f[b][i];
  }
  ans=min(ans,min(val[a][0],val[b][0]));
  return ans;
}
int main() {
  scanf("%d%d",&n,&m);
  for(int i=1;i<=m;++i) scanf("%d%d%d",&a[i].u,&a[i].v,&a[i].w);
  sort(a+1,a+1+m,cmp);
  for(int i=1;i<=n;++i) fa[i]=i;
  for(int i=1;i<=m;++i) {
    int x=a[i].u,y=a[i].v;
    x=find(x),y=find(y);
    if(x!=y) {
      fa[x]=y;
      ct(a[i].u,a[i].v,a[i].w);ct(a[i].v,a[i].u,a[i].w);    
    }
  }
  for(int i=1;i<=n;++i) {
    if(!vis[i]) {
      d[i]=1;
      dfs(i);
      val[i][0]=1020040222;
      f[i][0]=1;
    }
  }
  for(int j=1;j<=20;++j)
  for(int i=1;i<=n;++i)
  f[i][j]=f[f[i][j-1]][j-1],val[i][j]=min(val[i][j-1],val[f[i][j-1]][j-1]);
  scanf("%d",&p);
  while(p--) {
    scanf("%d%d",&x,&y);
    printf("%d\n",lca(x,y));
  } 
  return 0;
}

6. 洛谷P2342 叠积木

题目背景

\(Cube Stacking, 2004 Open\)

题目描述

约翰和贝西在叠积木。共有\(30000\)块积木，编号为\(1\)到\(30000\)。一开始，这些积木放在地上，自然地分成\(N\)堆。贝西接受约翰的指示，把一些积木叠在另一些积木的上面。一旦两块积木相叠， 彼此就再也不会分开了，所以最后叠在一起的积木会越来越高。约翰让贝西依次执行\(P\)条操作，操作分为两种：

 第一种是移动操作，格式为“移动\(X\)到\(Y\)的上面”。\(X\)和\(Y\)代表两块积木的编号，意思是将X所的那堆积木，整体叠放到\(Y\)所在的那堆积木之上；

 第二种是统计操作，格式为“统计\(Z\)下方的积木数量”。\(Z\)代表一块积木的编号，意思是贝西需要报告在编号为\(Z\)的积木之下还有多少块积木

请编写一个程序，帮助贝西回答每条统计问题。

输入输出格式

输入格式：

 第一行：单个整数：\(P，1 ≤ P ≤ 10^5\)

 第二行到第\(P + 1\)行：每行描述一条命令，如果这行开头的字母是 \(M\)，代表一条移动命令，后面的两个整数代表上文中的X和\(Y\)；如果开头字母是 \(C\)，代表一条统计命令。后面的整数代表上文中的\(Z\)，保证所有的移动命令都有意义，\(X\)和\(Y\)不会已经出现在同一堆积木里

输出格式：

 对每一个统计命令，输出正确回答，用换行符分开每个查询的结果

输入输出样例

输入样例#1：

6
M 1 6
C 1
M 2 4
M 2 6
C 3
C 4

输出样例#1：

1
0
2

说明

第一次查询时， \(1\) 下面只有一个 \(6\)；第二次查询时， \(3\) 下面没有任何积木；第三次查询时，\(4\) 下面有两块积木：\(1\) 和 \(6\)

思路：并查集的题目就是不一样，代码短小精悍，思路却很难想……对于这道题目来说，我们用一个\(s\)数组表示某个积木上方有多少个积木，再用一个数组\(a\)表示以某个点为顶的积木的个数，在并查集路径压缩的过程中让\(s[x]+=s[fa[x]]\)，就是说\(x\)的父亲是在\(x\)上面的，那么就把它父亲上面的积木也加到\(x\)上面来，然后对于每个移动命令，是把以\(x\)为顶的那一块放到\(y\)上面，那么我们就更新\(x\)是\(y\)的父亲，然后以\(x\)为顶的积木个数变成了原本以\(x\)为顶的积木个数加上原本以\(y\)为顶的积木个数，\(y\)上方的积木个数就加上了原本以\(x\)为顶的积木个数，然后对于每个统计命令，因为要求对于\(x\)输出\(x\)下面的积木的个数，那么就是以\(x\)为顶的积木个数减去\(x\)上面的积木个数再减\(1\)(因为\(x\)不在\(x\)的下方)。

代码：

#include<cstdio>
#include<iostream>
#include<cstring>
#define maxn 30007
using namespace std;
int p,fa[maxn],s[maxn],a[maxn];
string s1;
inline int qread() {
  char c=getchar();int num=0,f=1;
  for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
  for(;isdigit(c);c=getchar()) num=num*10+c-'0';
  return num*f;
}
int find(int x) {
  if(fa[x]==x) return x;
  int res=find(fa[x]);
  s[x]+=s[fa[x]];
  return fa[x]=res;
}
int main() {
  p=qread();
  for(int i=1;i<=30000;++i) a[i]=1,fa[i]=i;
  for(int i=1,x,y;i<=p;++i) {
    cin>>s1;
    if(s1=="M") {
      x=qread(),y=qread();
      int zrj=find(x),cyh=find(y);
      if(zrj!=cyh) {
        fa[cyh]=zrj;
        s[cyh]+=a[zrj];
        a[zrj]+=a[cyh];
        a[cyh]=0;
      }
    }
    else {
      x=qread();
      int zrj=find(x);
      printf("%d\n",a[zrj]-s[x]-1);
    }
  }
  return 0;
}

7. 洛谷 P1197 [JSOI2008]星球大战

题目描述

很久以前，在一个遥远的星系，一个黑暗的帝国靠着它的超级武器统治着整个星系。

某一天，凭着一个偶然的机遇，一支反抗军摧毁了帝国的超级武器，并攻下了星系中几乎所有的星球。这些星球通过特殊的以太隧道互相直接或间接地连接。

但好景不长，很快帝国又重新造出了他的超级武器。凭借这超级武器的力量，帝国开始有计划地摧毁反抗军占领的星球。由于星球的不断被摧毁，两个星球之间的通讯通道也开始不可靠起来。

现在，反抗军首领交给你一个任务：给出原来两个星球之间的以太隧道连通情况以及帝国打击的星球顺序，以尽量快的速度求出每一次打击之后反抗军占据的星球的连通块的个数。（如果两个星球可以通过现存的以太通道直接或间接地连通，则这两个星球在同一个连通块中）。

输入输出格式

输入格式：

输入文件第一行包含两个整数，\(N (1 \leq N \leq 2M)\) 和 \(M(1 \leq M \leq 200,000)\)，分别表示星球的数目和以太隧道的数目。星球用 \(0\) ~ \(N-1\) 的整数编号。

接下来的 \(M\) 行，每行包括两个整数 \(X\), \(Y\)，其中\(（ 0 < = X <> Y\) 表示星球 \(X\) 和星球 \(Y\) 之间有 “以太” 隧道，可以直接通讯。

接下来的一行为一个整数 \(k\) ，表示将遭受攻击的星球的数目。

接下来的 \(k\) 行，每行有一个整数，按照顺序列出了帝国军的攻击目标。这 \(k\) 个数互不相同，且都在 \(0\) 到 \(n-1\) 的范围内。

输出格式：

第一行是开始时星球的连通块个数。接下来的 \(k\) 行，每行一个整数，表示经过该次打击后现存星球的连通块个数。

输入输出样例

输入样例#1：

8 13
0 1
1 6
6 5
5 0
0 6
1 2
2 3
3 4
4 5
7 1
7 2
7 6
3 6
5
1
6
3
5
7

输出样例#1：

1
1
1
2
3
3

说明

\([JSOI2008]\)

思路：这道题目的思路非常巧妙，我们用一个\(vis\)数组来记录一下被破坏的星球，然后用一个\(h\)数组来保存被破坏星球的顺序，然后按给出边的顺序合并并查集，求出k次破坏星球后还剩下的联通块个数，然后倒序枚举一个\(i\)，依次还原\(k\)个星球，然后继续求联通块个数，用一个\(a\)数组分别记录\(k\)次还原后的联通块个数，然后输出即可。

代码：

#include<cstdio>
#include<algorithm>
#include<cctype>
#include<cstring>
#define maxn 400007
using namespace std;
int n,m,k,a[maxn],fa[maxn],num,h[maxn],head[maxn];
bool vis[maxn];
inline int qread() {
  char c=getchar();int num=0,f=1;
  for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
  for(;isdigit(c);c=getchar()) num=num*10+c-'0';
  return num*f;
}
struct node {
  int u,v,nxt;
}e[maxn];
inline void ct(int u, int v) {
  e[++num].u=u;
  e[num].v=v;
  e[num].nxt=head[u];
  head[u]=num;
}
int find(int x) {return fa[x]==x?x:fa[x]=find(fa[x]);}
inline void uni(int x, int y) {x=find(x),y=find(y);fa[y]=x;}
int main() {
  n=qread(),m=qread();
  for(int i=0;i<n;++i) fa[i]=i;
  for(int i=1,u,v;i<=m;++i) {
    u=qread(),v=qread();
    ct(u,v);ct(v,u);
  }
  scanf("%d",&k);
  int ltk=n-k;
  for(int i=1,x;i<=k;++i) {
    x=qread();
    vis[x]=1,h[i]=x;
  }
  for(int i=1;i<=(m<<1);++i) {
    int u=e[i].u,v=e[i].v;
    if(!vis[u]&&!vis[v]&&find(u)!=find(v)) uni(u,v),ltk--;
  }
  a[k+1]=ltk;
  for(int t=k;t>=1;--t) {
    int u=h[t];
    ltk++;
    vis[u]=0;
    for(int i=head[u];i;i=e[i].nxt) {
      int v=e[i].v;
      if(!vis[v]&&find(u)!=find(v)) uni(u,v),ltk--;
    }
    a[t]=ltk;
  }
  for(int i=1;i<=k+1;++i) printf("%d\n",a[i]);
  return 0;
}