线性方程 Ax=b 是稳定状态的问题,特征值在动态问题中有着巨大的重要性。 du/dt=Au 的解随着时间增长、衰减或者震荡,是不能通过消元来求解的。接下来,我们进入线性代数一个新的部分,基于 Ax=λx,我们要讨论的所有矩阵都是方阵。
1. 特征值和特征向量
几乎所有的向量在乘以矩阵 A 后都会改变方向,某些特殊的向量 x 和 Ax 位于同一个方向,它们称之为特征向量。
Ax=λx
数字 λ 称为特征值。它告诉我们在乘以 A 后,向量是怎么被拉伸、缩小、反转或者不变的。 λ=0 意味着特征向量存在于矩阵的零空间中。任意向量都是单位矩阵的特征向量,因为 Ix=x,其特征值为 1。
要计算特征值的话,我们只需要知道 det(A−λI)=0 即可。
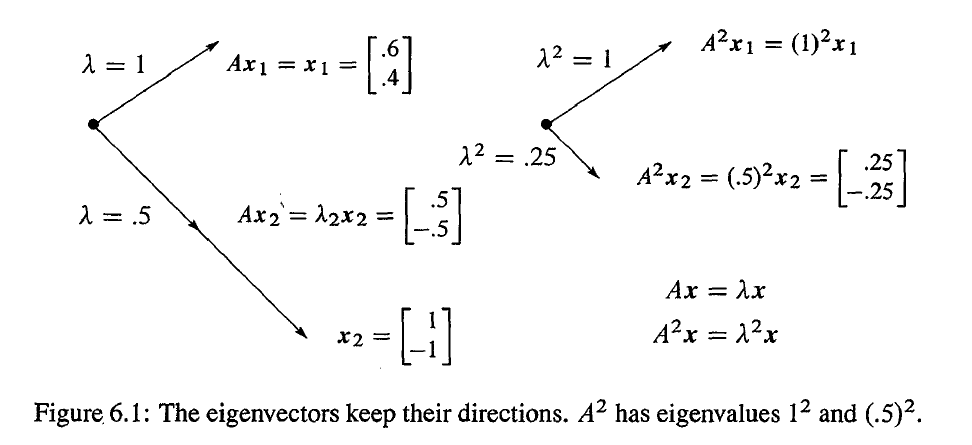
如果 x1 乘以 A 的话,我们仍然得到 x1,任意 A 的乘方仍然得到 Anx1=x1 。如果 x2 乘以 A 的话,我们得到 21x2,再乘以 A 我们得到 (21)2x2。
当 A 被平方的时候,其特征向量不变,特征值也变为平方。
这种模式将会继续保持,因为特征向量一直待在他们自己的方向,不会改变。
其它向量都会改变方向,但它们可以表示为特征向量的线性组合。
当我们将这个向量乘以 A 后,每个特征向量都乘以了它们对应的特征值。
利用这个特性,我们可以进行 99 次乘法。
特征向量 x1 处于稳定状态,因为 λ1=1,所以它不会改变。特征向量 x2 处于衰减状态,因为 λ2=0.5,乘方次数很大时,它就相当于消失了。
上述这个特殊的矩阵是一个马尔科夫矩阵,它的每个元素都为正并且每一列相加之后和为 1,这保证了它的最大特征值为 1。
对于投影矩阵,它的特征值为 0 和 1。 λ=1 对应于稳定状态,投影矩阵将列空间的所有向量都投影到列空间中去,也即还是它自身, Px1=x1。 λ=0 对应于零空间,投影矩阵将零空间的所有向量都投影到零向量, Px2=0。
对于镜像矩阵,它的特征值为 1 和 -1。 λ=1 说明乘以矩阵 R 后特征向量 x1 不变, λ=−1 说明乘以矩阵 R 后特征向量 x2 变为相反方向。
同时,由于 R=2P−I,因此投影矩阵和镜像矩阵有着相同的特征向量。如果 Px=λx,那么
(2P−I)x=2Px−Ix=(2λ−1)x
2. 特征值的计算
Ax=λx→(A−λI)x=0
如果上述式子有非零解,那么 A−λI 是奇异的,也就是行列式为零。因此,我们先通过下式求出特征值。
det(A−λI)=0
然后,针对每个特征值,再通过求解 (A−λI)x=0 来找到特征向量。
一些 2×2 矩阵可能只有一个特征向量,这时候,它的两个特征值相同。同理, n×n 的矩阵如果没有 n 个线性不相关的特征向量,那么就不能将任意一个向量都表示为特征向量的线性组合。
消元过程通常会改变矩阵的特征值,三角型矩阵 U 的对角线元素即为特征值,但它们不是矩阵 A 的特征值。
但是,我们可以从矩阵中很快地就发现特征值的乘积以及和。
n 个特征值的乘积就是矩阵的行列式值。 n 个特征值的和就是矩阵 n 个对角线元素的和。
主对角线上元素的和称为矩阵的迹(trace)。
另外,特征值也可能会不是实数。
获取更多精彩,请关注「seniusen」!




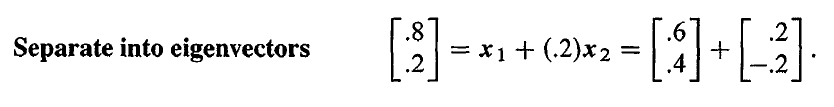
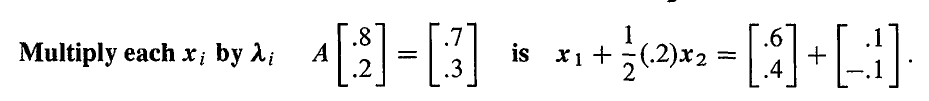


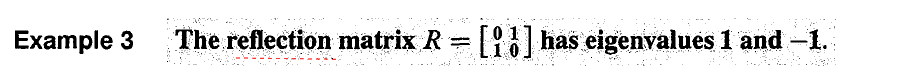




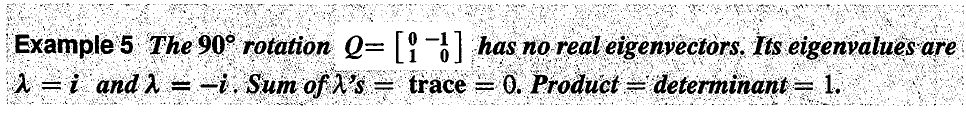
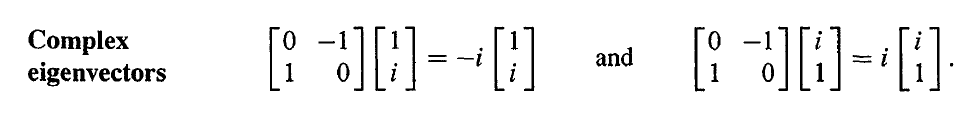


 京公网安备 11010502036488号
京公网安备 11010502036488号