2022-04-20：小团去参加军训，军训快要结束了， 长官想要把大家一排n个人分成m

2022-04-20：小团去参加军训，军训快要结束了， 长官想要把大家一排n个人分成m组，然后让每组分别去参加阅兵仪式， 只能选择相邻的人一组，不能随意改变队伍中人的位置， 阅兵仪式上会进行打分，其中有一个奇怪的扣分点是每组的最大差值， 即每组最大值减去最小值， 长官想要让这分成的m组总扣分量最小，即这m组分别的极差之和最小。 长官正在思索如何安排中，就让小团来帮帮他吧。

答案2022-04-20：

动态规划。 时间复杂度：O(M * N * N)。

代码用rust编写。代码如下：

use rand::Rng;

fn main() {
    let mut arr: Vec<isize> = vec![];
    let n = rand::thread_rng().gen_range(10, 30);
    println!("n = {}", n);
    for i in 0..n {
        arr.push(rand::thread_rng().gen_range(1, 1000));
    }
    println!("arr = {:?}", arr);
    let m = rand::thread_rng().gen_range(1, n);
    println!("m = {}", m);
    let ret = min_score2(&mut arr, m);
    println!("ret = {}", ret);
}

fn min_score2(arr: &mut Vec<isize>, m: isize) -> isize {
    if m == 0 {
        return 0;
    }
    let n: isize = arr.len() as isize;
    let mut score: Vec<Vec<isize>> = vec![];
    for i in 0..n {
        score.push(vec![]);
        for j in 0..n {
            score[i as usize].push(0);
        }
    }
    for i in 0..n {
        let mut max = arr[i as usize];
        let mut min = arr[i as usize];
        score[i as usize][i as usize] = max - min;
        for j in i + 1..n {
            max = get_max(max, arr[j as usi*** = get_min(min, arr[j as usize]);
            score[i as usize][j as usize] = max - min;
        }
    }
    let mut dp: Vec<Vec<isize>> = vec![];
    for i in 0..m + 1 {
        dp.push(vec![]);
        for j in 0..n {
            dp[i as usize].push(0);
        }
    }
    for i in 0..n {
        dp[1][i as usize] = score[0][i as usize];
    }
    for split in 2..=m {
        for i in split..n {
            dp[split as usize][i as usize] = dp[(split - 1) as usize][i as usize];
            for j in 1..=i {
                dp[split as usize][i as usize] = get_min(
                    dp[split as usize][i as usize],
                    dp[(split - 1) as usize][(j - 1) as usize] + score[j as usize][i as usize],
                );
            }
        }
    }
    //println!("dp = {:?}", dp);
    return dp[m as usize][(n - 1) as usize];
}

fn get_max(a: isize, b: isize) -> isize {
    if a > b {
        a
    } else {
        b
    }
}

fn get_min(a: isize, b: isize) -> isize {
    if a < b {
        a
    } else {
        b
    }
}

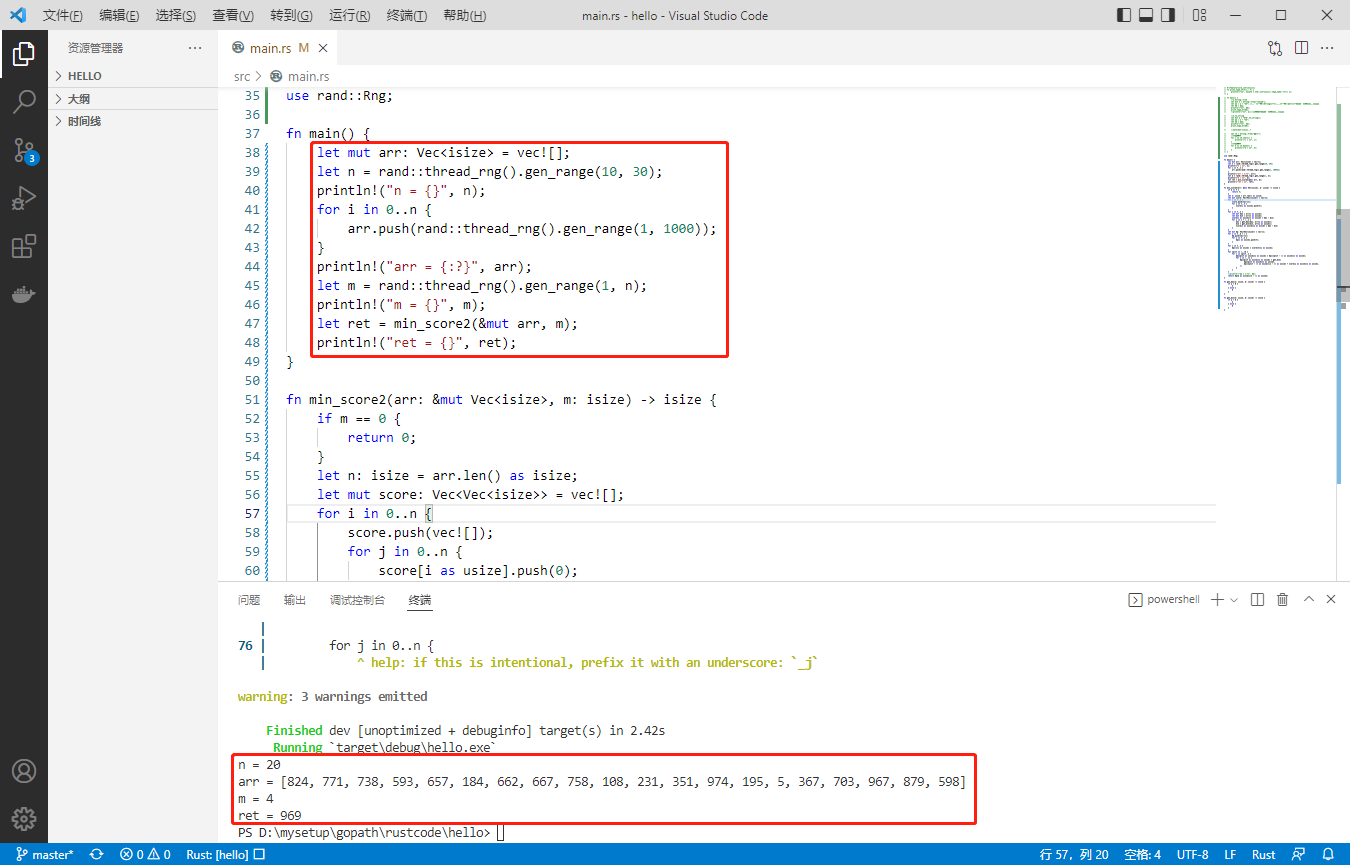
执行结果如下：

左神java代码