本节的核心是将常系数微分方程转化为线性代数问题。
dtdu=λu的解为u(t)=Ceλt
代入 t=0,可得 u(0)=C,因此有 u(t)=u(0)eλt。这是只有一个变量的情况,在线性代数里,我们扩展到 n 个方程的情况。
dtdu=Au初始条件为向量u(0)t=0
注意,这里 A 是常矩阵,不随时间而改变。而且这些方程是线性的,如果 u(t) 和 v(t) 都是方程组的解,那么它们的线性组合 Cu(t)+Dv(t) 也是解,我们需要 n 个这样的常数来匹配方程组的初始条件。
1. dtdu=Au 的解
其中一个解是 eλtx, λ 是矩阵 A 的特征值,而 x 是特征向量。将这个解代入原方程,利用 Ax=λx 可得
dtdu=λeλtx=Aeλtx=Au
这个解的所有部分都有 eλt,当 λ>0 时,解会增长;当 λ<0 时,解会衰减。而当 λ 为虚数时,则它的实部决定解是增长还是衰减。
求解 dtdu=Au=[0110]u,u0=[42]。
矩阵 A 的特征值为 1 和 -1,特征向量为 (1, 1) 和 (1, -1),因此两个纯指数解为:
u1(t)=eλ1tx1=et[11]
u2(t)=eλ2tx2=e−t[1−1]
这些 u 依然是矩阵的特征向量,它们满足 Au1=u1 和 Au2=−u2,只不过是系数随着 t 改变罢了。方程组的全解为这些特解的线性组合。

利用初始条件我们可以确定出系数 C 和 D。
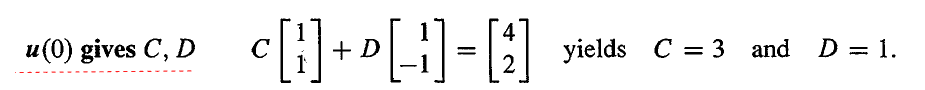
因此,我们可以通过以下三个步骤来求解 dtdu=Au。
- 将 u0 写成特征向量的线性组合, u0=c1x1+⋯+cnxn;
- 将每个特征向量 xi 乘以 eλit;
- 全解就是 eλtx 的线性组合, u(t)=c1eλ1tx1+⋯+cneλntxn。
注意,如果两个特征值相同而只有一个对应的特征向量,那么我们就需要另外一个解 teλtx。

2. 二阶方程组
针对二阶方程 my′′+by′+ky=0,我们将之转化为矩阵形式,假设 m=1。

因此,我们需要先求解出矩阵的特征值和特征向量。

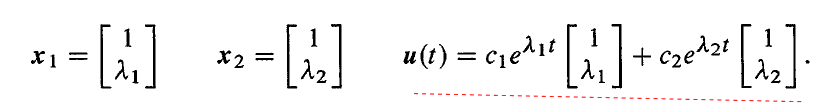
3. 2×2 矩阵的稳定性
针对方程组的解,我们想知道随着 t→∞,解是否趋向于 u=0,也就是问题是否是稳定的。这取决于矩阵的特征值。
全解是由 eλtx 构建出来的。如果特征值 λ 是实数,只有当 λ<0 时,解才会趋向 0。如果特征值 λ 是复数,那么有 λ=r+is,那么其实部必须小于零。
对 2×2 矩阵 [acbd] 来说,如果其两个特征值满足上面的两个条件,则一定有:
λ1+λ2<0→矩阵的迹T=a+d<0
λ1λ2>0→矩阵的行列式D=ad−bc>0
4. 矩阵的指数次方
最后,我们想将方程组的解写成一个新的形式 u(t)=eAtu0。
ex=1+x+21x2+61x3+⋯
我们将 x 换成矩阵,可得:
eAt=I+At+21(At)2+61(At)3+⋯
它的导数为 AeAt:
A+A2t+21A3t2+61A4t3+⋯=AeAt
它的特征值是 eλt:
(I+At+21(At)2+61(At)3+⋯)x=(1+λt+21(λt)2+61(λt)3+⋯)x
假设 A 有 n 个线性不相关的特征向量,将 A=SΛS−1 代入 eAt 可得:
eAt=I+At+21(At)2+61(At)3+⋯
=I+SΛS−1t+21(SΛS−1t)(SΛS−1t)+⋯
将 S 和 S−1 提取出来有
=S(I+Λt+21(Λt)2+⋯)S−1=SeΛtS−1
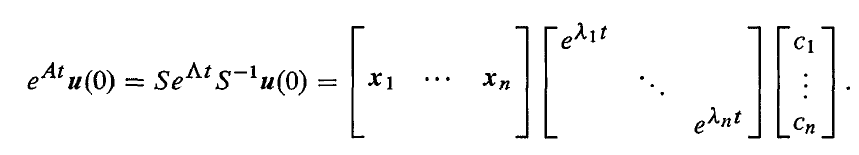
这和之前解的形式是一模一样的!
- 例 3

eAt 满足下面三个规则:
-
eAt 总有逆矩阵 e−At;
-
eAt 的特征值总是 eλt;
-
如果 A 是反对称矩阵,即 AT=−A,那么 e−At 是一个正交矩阵,转置等于逆。
-
例 4
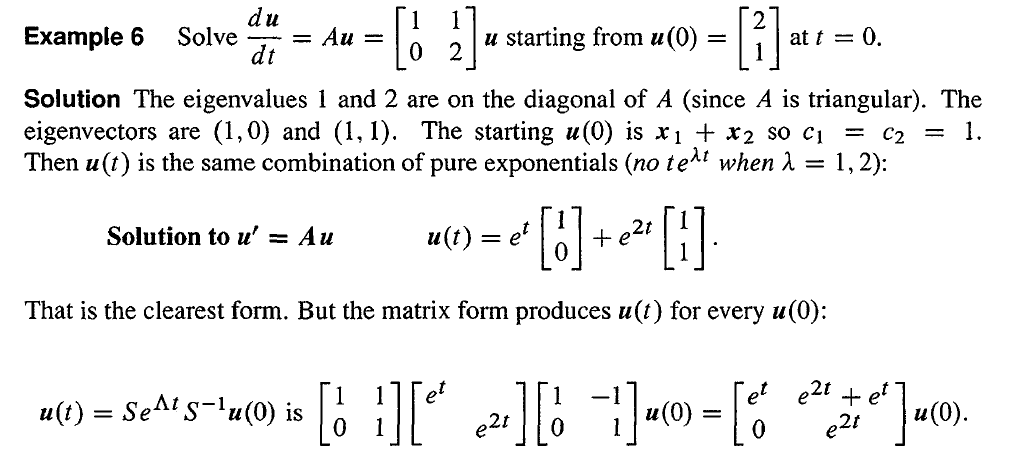
获取更多精彩,请关注「seniusen」!





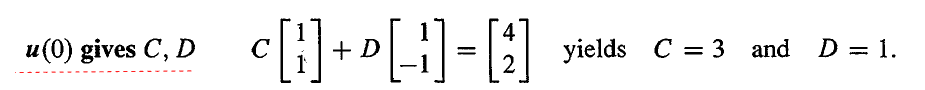



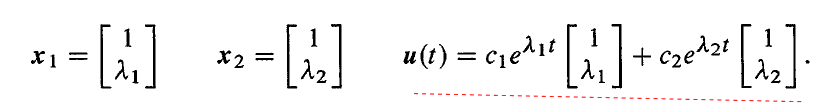
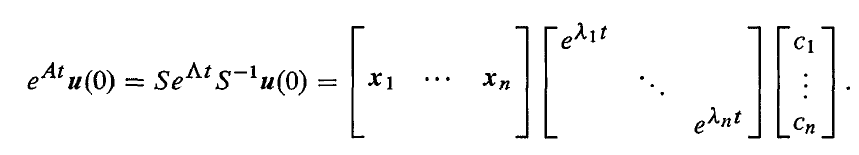

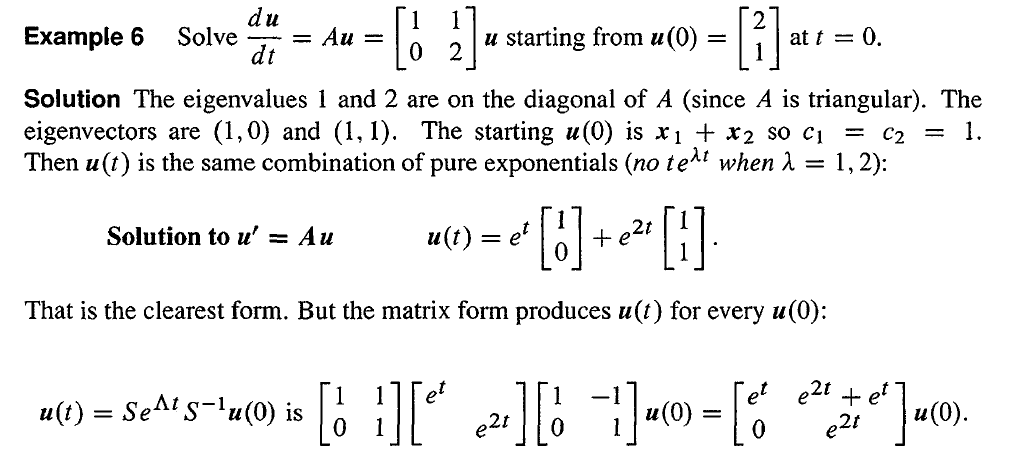


 京公网安备 11010502036488号
京公网安备 11010502036488号