2019牛客多校7月18日第一场

A

题意

RMQ(A, l, r)定义为A[l…r]中最小的元素的下标。
重新定义了两个数组相等的含义。
定义为两个数组相等为任意相同方式的切片[l:r]的RMQ值相等。
给定两个数组，选一个最大的p，满足数组a[1…p]和b[1…p]相等。

题解

使用单调栈。

单调栈（以递增栈为例）

具体算法

1. 栈中人为置入无穷小元素（比正常元素都小）
2. 元素a[1…n]一个个尝试入栈，但无法符合递增栈要求时栈顶出栈直到可以入栈为止
3. 入栈

性质

当a数组每个元素各不相同的时候。
如此，任意时刻对栈进行快照。假设栈为如此

…a[i],a[j],…
栈底 栈顶

1. 栈递增有 $a\left[j\right]\>a\left[i\right]$a[j]>a[i]、
2. a[i],a[j]之间任意一个元素a[k]都大于a[j].这点其实也不难想到，显然a[k]曾经如果栈，现在不在了，那么a[k]一定是被它后面的元素踢走了。x被y踢走，说明 $x\>y$x>y.而踢走它的元素也会被他后面的元素踢走，于是会形成一条踢人被踢的链条。 $a\left[k\right]-\>a\left[k_1\right]-\>a\left[k_2\right]-\>...-\>a\left[j\right]$a[k]−>a[k1​]−>a[k2​]−>...−>a[j]，最终踢人的就是a[j]。而不等式是有传递性的，所以最终会有 $a\left[k\right]\>a\left[j\right]$a[k]>a[j]

此题分析

两个数组定义的相等，容易发现，说白了就是a[i]在a数组的排名和b[i]在b数组的排名要一样。就是相对大小的变化要一致。
我们按照上面的单调栈的操作做法对a数组进行入栈，并记录每个元素入栈时在栈中的下标，得一个数组A。b数组同理，得数组B。
那么A[1…p]与B[1…p]普通意义下的数组相等等价于a[1…p]与b[1…p]在题目定义的数组相等。
可以用数学归纳法想，p=1显然成立。
假设对于p已经成立，对于p+1可以用数学证明。
不过我加了一张图以易于理解一些。
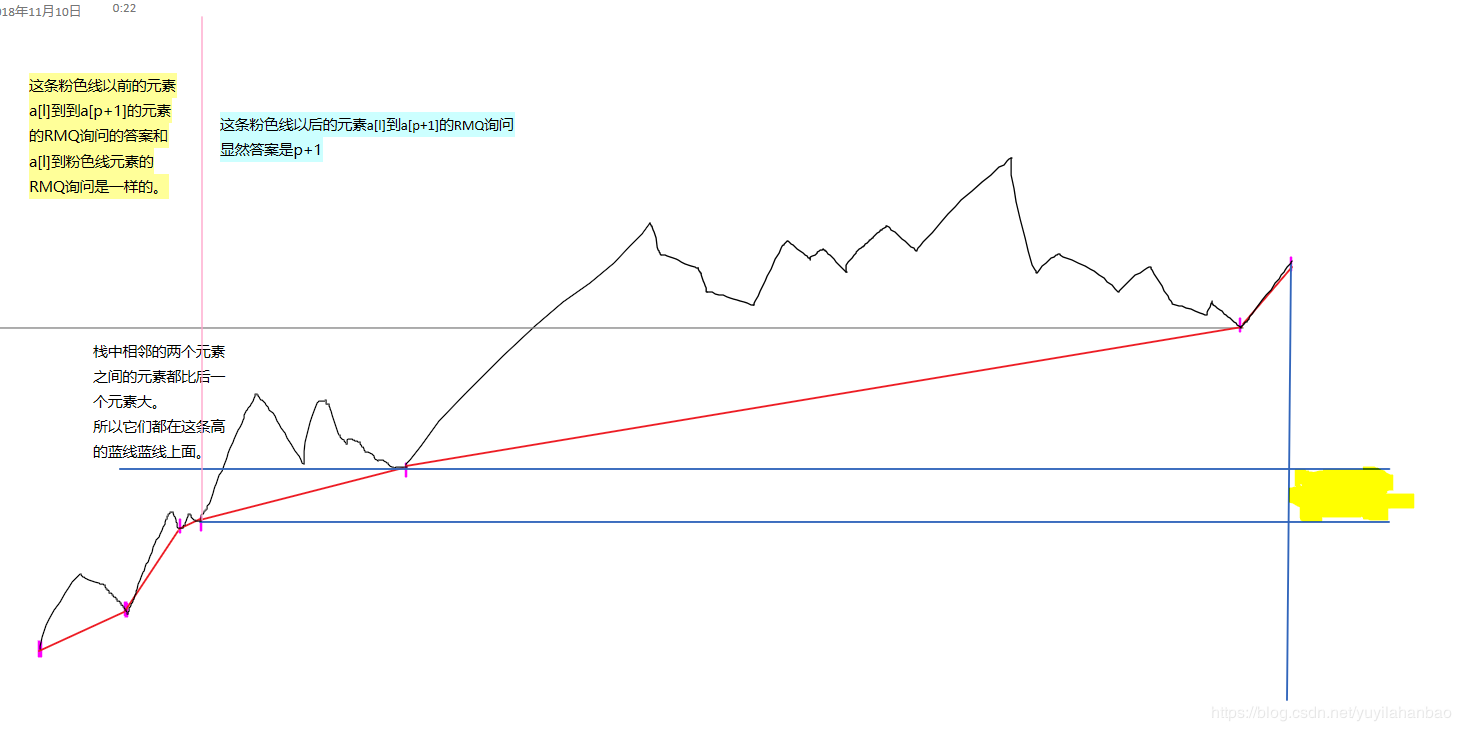
如图，蓝色竖线之前的是前p个元素的大小元素。因为a与b在题目定义下的相等只需要考虑排名（相对大小）。而对于前p个元素已经保证相对大小情况一致了，所以它们的大小情况可以用同一张图。
红色点从左到右是栈从底到顶的元素。
黄***域是a[p+1]的位置。
由于前p个已经保证想等了，所以只需要考虑 $r=p+1$r=p+1的RMQ询问，这个分了两种情况如图。
如果 $A[p+1]=B[p+1]$A[p+1]=B[p+1]，则a[p+1]和b[p+1]落入同一个区域，那么，两种情况的RMQ询问答案肯定是相同的。

即 $A[\mathrm{1..}p+1]=B[\mathrm{1..}p+1]\Rightarrow a[\mathrm{1..}p+1]=b[\mathrm{1..}p+1]$A[1..p+1]=B[1..p+1]⇒a[1..p+1]=b[1..p+1]

如果 $A[p+1]\ne B[p+1]$A[p+1]̸​=B[p+1]，显然 $a[\mathrm{1..}p+1]\ne b[\mathrm{1..}p+1]$a[1..p+1]̸​=b[1..p+1].
即 $A[\mathrm{1..}p+1]=B[\mathrm{1..}p+1]\Rightarrow a[\mathrm{1..}p+1]=b[\mathrm{1..}p+1]$A[1..p+1]=B[1..p+1]⇒a[1..p+1]=b[1..p+1]
因此，是等价的。