这部分我们有两个目标。一是了解正交性是怎么让 x^ 、 p 、 P 的计算变得简单的,这种情况下, ATA 将会是一个对角矩阵。二是学会怎么从原始向量中构建出正交向量。
1. 标准正交基
向量 q1,⋯,qn 是标准正交的,如果它们满足如下条件:
qiTqj={0,1,if i̸=j(正交向量)if i=j(单位向量)
如果一个矩阵的列是标准正交的,我们称之为 Q。很容易,我们可以得到 QTQ=I。

当 Q 是方阵的时候,我们可以得到 QT=Q−1,也即转置等于逆。

旋转矩阵 Q 就是将任意向量逆时针旋转 θ,其逆矩阵 Q−1 就是将任意向量顺时针旋转 θ。


置换矩阵的作用就是交换矩阵的行,在消元的时候有很大的作用。
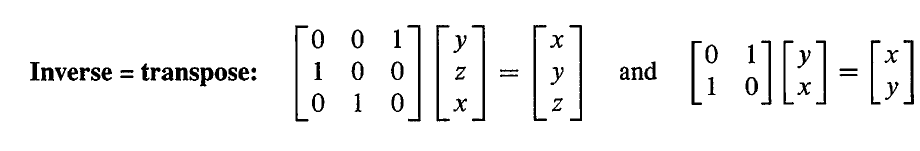
如果 u 是任意单位向量,那么 Q=I−2uuT 是一个正交矩阵。

Q2=QTQ=I
绕对称轴镜像两次还是它本身。
取 u1=(1,0), u2=(1/2 ,−1/2 ),然后,我们可以得到两个正交矩阵。
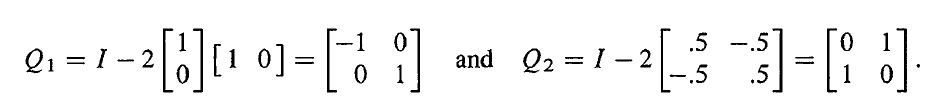
Q1 将任意向量 (x,y) 变为 (−x,y), y 轴是镜像轴。 Q2 将任意向量 (x,y) 变为 (y,x), 45° 轴是镜像轴。

可以看到,旋转、置换和镜像都不会改变一个向量的长度。实际上,乘以任意正交矩阵都不会改变向量的长度。
∣∣Qx∣∣=∣∣x∣∣
∣∣Qx∣∣2=(Qx)T(Qx)=xTQTQx=xTIx=∣∣x∣∣2
而且,正交矩阵也会保留两个向量的点积。
(Qx)T(Qy)=xTQTQy=xTy
2. 正交矩阵的投影
当矩阵 A 变成了正交矩阵 Q,那么投影就会变得非常简单,我们不需要求任何逆矩阵。
ATAx^=ATb→x^=QTb
p=Ax^→p=Qx^=QQTb
P=A(ATA)−1AT→P=QQT
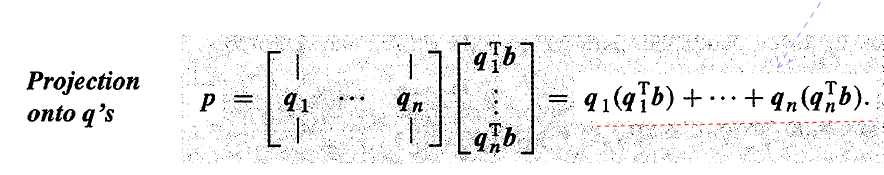
当 Q 为方阵的时候,子空间为整个空间,有 QT=Q−1。 x^=QTb 就等同于 x=Q−1b,也就是有唯一解, b 的投影即为它本身。

这就是傅里叶变化和所有应用数学中各种变化的基础,它们将向量或者函数分解成正交的小片,将这些小片加起来之后就回到了原函数。

3. Gram-Schmidt 正交化和 A 的 QR 分解
从上面我们可以看到正交对我们是非常有利的,现在我们就要找到一个方法来创造出标准正交的向量。假设我们有三个不相关的向量 a,b,c,如果我们能构造出正交的三个向量 A,B,C,那么再除以它们的长度就得到了标准正交向量。
首先,我们选取 A=a,那么 B 必须垂直于 A 。我们用 b 减去其在 A 的投影,就得到了垂直于 A 的部分,这也就是我们要找的 B。
B=b−ATAATbA
接着,我们再用 c 减去其在 A 和 B 的投影,就得到我们要找的 C。
C=c−ATAATcA−BTBBTcB
如果我们有更多的向量,那我们就用新的向量减去它在已经设定好的所有向量上的投影即可,最后,我们再除以它们各自的长度就得到了标准正交向量。

可以看到, q1=a/∣∣a∣∣,没有涉及到其它向量, a、 q1、 A 都位于一条线上。第二步中 b 也只是 A 和 B 的线性组合,不涉及到后面的向量, a,b、 q1,q2、 A,B 都位于一个平面内。在每一个步骤中, a1,a2,⋯,ak 只是 q1,q2,⋯,qk 的线性组合,后面的 q 没有涉及到。
联系 A 和 Q 的矩阵 R 是上三角形矩阵,有 A=QR。

任意 m×n 的矩阵 A,如果其列是不相关的,那么就可以分解成 QR, Q 的列是标准正交的,而 R 是上三角矩阵并且对角线元素为正,为向量 ⋯B,C⋯ 的长度。
然后,最小二乘就变成了
ATAx^=ATb→RTQTQRx^=RTQTb→RTRx^=RTQTb→Rx^=QTb→x^=R−1QTb
获取更多精彩,请关注「seniusen」!









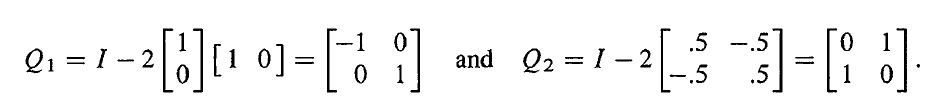

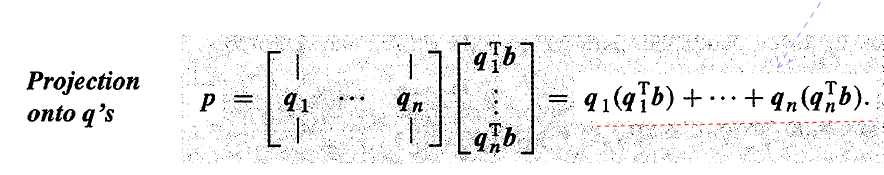






 京公网安备 11010502036488号
京公网安备 11010502036488号