描述
题目描述
首先给定我们一个真分数 -- 就是分子要比我们的分母小, 然后我们这里给定的数据不一定上下的, 然后让我们转换为埃及分数, 什么是埃及分数呢, 我们可以知道如果一个分数的分子是的话, 我们的这个分数就可以被称之为是埃及分数
题解
解法一: 找规律取巧
实现思路
这个一个关键点就是我们把我们的字符串的以分号分隔然后计算出来上下的值是多少, 我们可以分母不变, 输出分子个数的分母分之一
代码实现
#include <bits/stdc++.h>
using namespace std;
signed main() {
string s;
while (cin >> s) {
int up = 0, down = 0;
// up是我们分号上面的数字, down是我们分号下面的数字
int pos = 0;
// 这个是我们的位置
for (; pos < s.size(); pos++) {
if (s[pos] == '/') {
pos += 1;
break;
// 如果我们到了分号的这个位置, 我们跳出这个循环
}
up = up * 10 + (s[pos] - '0');
// 我们计算我们的分号上面的数字大小是多少
}
for (; pos < s.size(); pos++) {
down = down * 10 + (s[pos] - '0');
// 这个是计算我们的分号下面数字是多少
}
for (int i = 1; i <= up; i++) {
cout << "1/" << down << "+\n"[i == up];
}
// 我们直接取巧的输出
}
return 0;
}
时空复杂度分析
时间复杂度:
理由如下: 事实上我们就是遍历了一次我们的这个字符串的长度
空间复杂度:
理由如下: 我们只使用了常数级别的空间
解法二: 正常的数学推导
实现思路
我们有这样的一个真分数, 那么我们可以得到这样的一个式子
, 所以我们
那么我们可以这样推导一下:
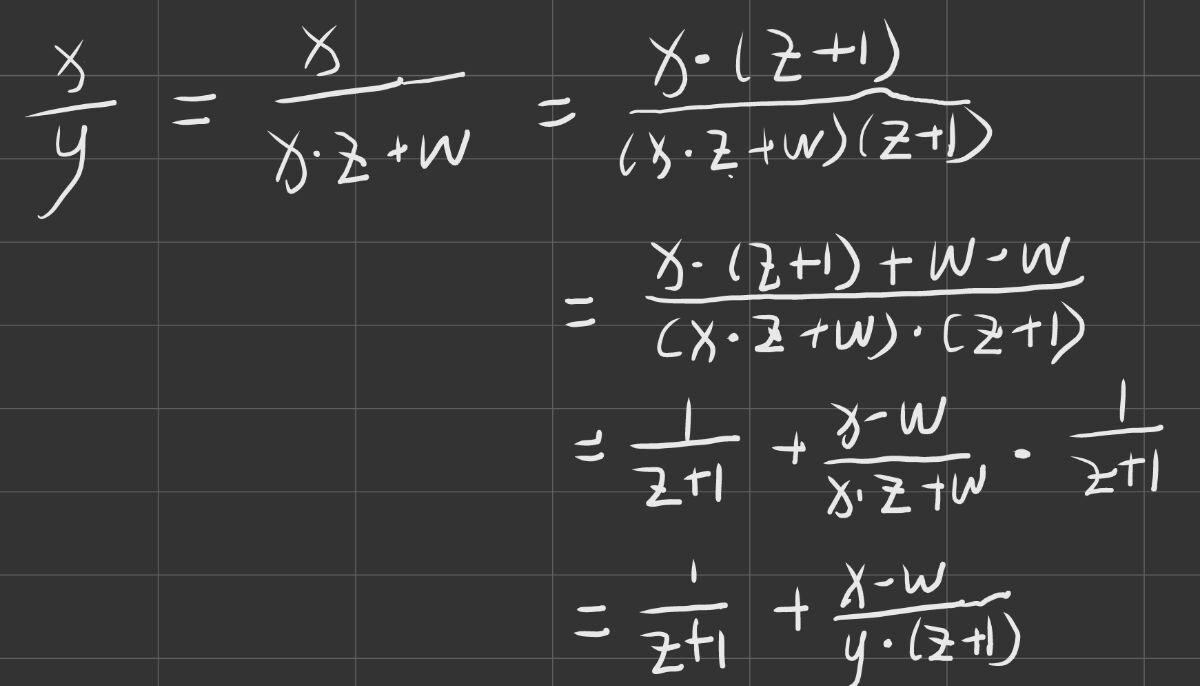
然后我们再令,
直到我们或者分母可以整除分子停止
代码实现
#include <bits/stdc++.h>
using namespace std;
void dfs(long long x, long long y) {
if (x == 1) {
cout << "1/" << y << "\n";
return;
}
if (y % x == 0) {
cout << "1/" << y / x << "\n";
return;
}
// 上面的两个条件是我们的递归终止的边界条件
long long shang = y / x, yu = y % x;
// 求取我们的商和余数
cout << "1/" << shang + 1 << "+";
// 输出
x -= yu, y *= (shang + 1);
// 更新我们的x和y
dfs(x, y);
}
signed main() {
string s;
while (cin >> s) {
long long up = 0, down = 0;
// up是我们分号上面的数字, down是我们分号下面的数字
int pos = 0;
// 这个是我们的位置
for (; pos < s.size(); pos++) {
if (s[pos] == '/') {
pos += 1;
break;
// 如果我们到了分号的这个位置, 我们跳出这个循环
}
up = up * 10 + (s[pos] - '0');
// 我们计算我们的分号上面的数字大小是多少
}
for (; pos < s.size(); pos++) {
down = down * 10 + (s[pos] - '0');
// 这个是计算我们的分号下面数字是多少
}
dfs(up, down);
}
return 0;
}
时空复杂度分析
时间复杂度:
理由如下: 我们最坏情况下, 我们会递归分子的次数, 所以我们最坏情况下是
空间复杂度:
理由如下: 我们系统递归栈的一个深度






 京公网安备 11010502036488号
京公网安备 11010502036488号