拆点和拆边
一、总述
在图论中,一张图由点和边构成。而点和边都可以作为信息的载体,比如说点权和边权。尽管点和边看似如此接近,但是它们的性质确实截然不同的。点表示的是一种实质上的状态,而边表示的是一种虚拟的状态间的转移。
因此,有一些图论算法只能处理点上的信息,而另一些图论算法只能处理边上的信息。怎样使得这些针对性的算法通用化呢?某些情况下,我们可以通过拆点和拆边的方式来解决。
二、常见的有针对性的算法
针对点权
- 树链剖分(套线段树或树状数组)
- Link-Cut Tree
- 倍增
- 强连通分量缩点
针对边权
- 最短路
- 最小生成树
- 网络流
- 匈牙利算法
- 拓扑排序
容易看出,数据结构型的算法一般针对点权,因为维护的是实体上的数据;而图论算法一般容易维护边权,因为在点与点之间通过边转移时,容易将边权一起转移走。
由于无向边可以当做两条有向边,因此下文均以有向边介绍。
三、拆点
过程
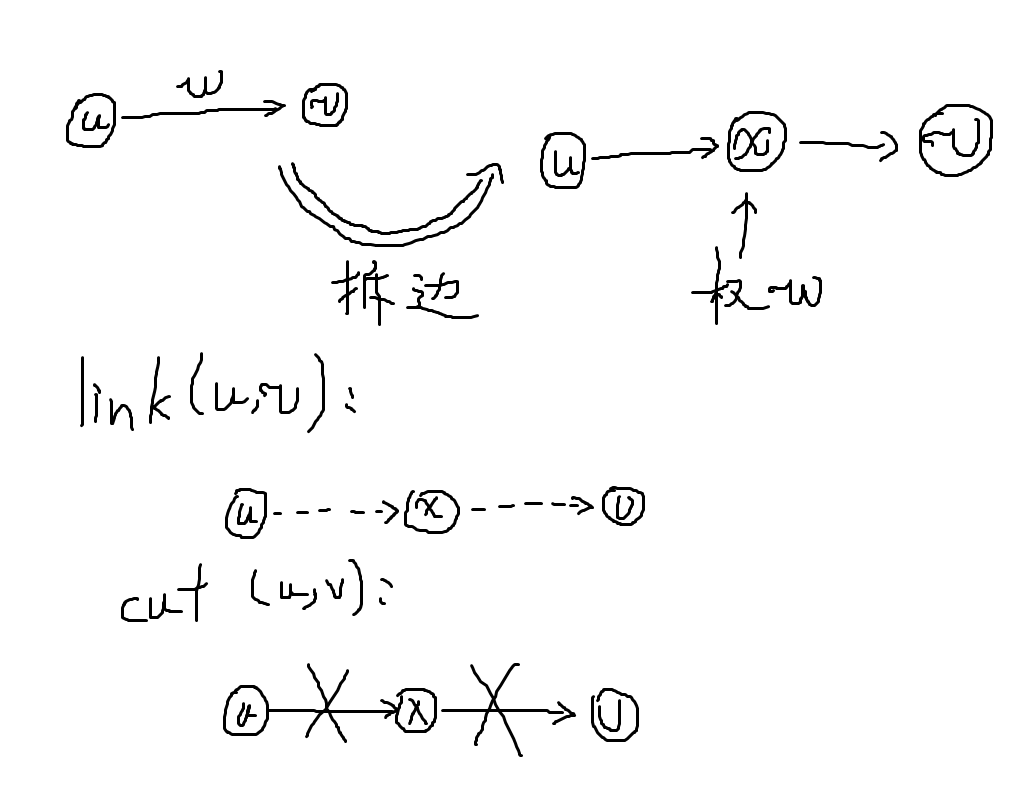
对于某个点权为 \(w\) 的点 \(v\),我们可以把 \(v\) 点拆成 \(v_1\) 和 \(v_2\) 两个点,其中 \(v_1\) 称为入点,\(v_2\) 称为出点。从 \(v_1 \to v_2\) 连一条权值为 \(w\) 的有向边。此外对于图上原本连接某两点 \(x\) 和 \(y\),权值为 \(z\) 的有向边,改为从 \(x_2 \to y_1\) 连权值为 \(z\) 的边。这就是拆点的主要过程。
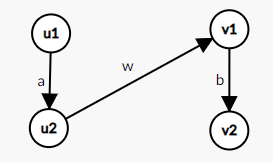
上图说明了拆点的过程。
实例
带点权和边权的最短路
其实这个不用拆点也能做,就用这个来作为拆点的入门好了。
有一张 \(n\) 个点,\(m\) 条边的有向图,点有点权,边有边权。定义一条路径的长度为这条路径经过的所有点的点权和加上经过的所有边的边权和。求 \(1\) 号点到 \(n\) 号点的最短路。
将点拆成入点和出点,从入点向出点连权值为该点点权的边。直接跑一遍起点为 \(1\) 号点的入点,终点为 \(n\) 号点的出点的单源最短路即可。
void solve() {
cin >> N >> M;
for (int i = 1; i <= N; ++i) {
int x; cin >> x; // 输入 i 点点权
add_edge(i, i + N, x);
}
for (int i = 1; i <= M; ++i) {
int u, v, w; // 一条从 u 到 v 权值为 w 的单向边
cin >> u >> v >> w;
add_edge(u + N, v, w);
}
Dijkstra(1); // 做一次源点为 1 的单源最短路径
printf("%d\n", dis[N + N]); // N 号点的出点的距离即为答案
}网络流
网络流上的流量都在边上,因此网络流属于针对边权的典型图论算法。当点上有权值时,都以拆点的形式解决。
直接举一道例题 方格取数加强版
给出一个 \(n \times n\) 的矩阵,每一格有一个非负整数 \(A_{i, j}\) \((A_{i, j} \le 1000)\)。现在从 \((1,1)\) 出发,可以往右或者往下走,最后到达 \((n,n)\)。每达到一格,把该格子的数取出来,该格子的数就变成 \(0\),这样一共走 \(K\) 次,现在要求 \(K\) 次所达到的方格的数的和最大。
很明显,这里的权值在点上。考虑拆点,将每个点拆成入点和出点。
由于每个格子的数只能取一次,因此我们从入点向出点连一条流量为 \(1\),权值为 \(A_{i, j}\) 的边。由于可以无数次经过,再从入点向出点连流量为 \(\infty\),权值为 \(0\) 的边。
同时为了转移,我们从一个格子的出点向其右方、下方的格子的入点连流量为 \(\infty\),权值为 \(0\) 的边。
最后求解原图上 \((1, 1)\) 的入点到 \((n, n)\) 的出点的流量为 \(K\) 的最小费用流即可。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
#include <queue>
using namespace std;
struct edge {
int to,cap,cost,rev;
};
typedef pair<int,int> P;
const int maxn=5000, INF=0x7F7F7F7F;
int n;
vector <edge> G[maxn+1];
edge make_edge(int to, int cap, int cost, int rev) {
edge x;
x.to=to, x.cap=cap, x.cost=cost, x.rev=rev;
return x;
}
void add_edge(int from, int to, int cap, int cost) {
G[from].push_back(make_edge(to,cap,cost,G[to].size()));
G[to].push_back(make_edge(from,0,-cost,G[from].size()-1));
}
int make_crn(int x, int y) {
return (x-1)*n+y;
}
void init(int &f) {
scanf("%d%d",&n,&f);
for (int i=1; i<=n; i++)
for (int j=1; j<=n; j++) {
int x;
scanf("%d",&x);
add_edge(make_crn(i,j),make_crn(i,j)+n*n,1,-x);
add_edge(make_crn(i,j),make_crn(i,j)+n*n,INF,0);
}
for (int i=1; i<=n; i++)
for (int j=1; j<n; j++)
add_edge(make_crn(i,j)+n*n,make_crn(i,j+1),INF,0);
for (int i=1; i<n; i++)
for (int j=1; j<=n; j++)
add_edge(make_crn(i,j)+n*n,make_crn(i+1,j),INF,0);
}
namespace EK_SPFA {
int dis[maxn+1];
int prev[maxn+1];
int pree[maxn+1];
void bfs(int s) {
bool mark[maxn+1];
queue <int> q;
memset(dis,0x7F,sizeof(dis));
memset(mark,0,sizeof(mark));
memset(prev,-1,sizeof(prev));
memset(pree,-1,sizeof(pree));
dis[s]=0;
mark[s]=true;
q.push(s);
while (!q.empty()) {
int x=q.front();
q.pop();
mark[x]=false;
for (int i=0; i<G[x].size(); i++) {
edge &e=G[x][i];
if (e.cap>0&&dis[x]+e.cost<dis[e.to]) {
dis[e.to]=dis[x]+e.cost;
prev[e.to]=x;
pree[e.to]=i;
if (!mark[e.to]) {
mark[e.to]=true;
q.push(e.to);
}
}
}
}
}
int min_cost_flow(int s, int t, int f) {
int cost=0;
while (f>0) {
bfs(s);
if (dis[t]==INF) return -1;
int d=f;
for (int i=t; prev[i]!=-1; i=prev[i])
d=min(d,G[prev[i]][pree[i]].cap);
f-=d;
cost+=d*dis[t];
for (int i=t; prev[i]!=-1; i=prev[i]) {
edge &e=G[prev[i]][pree[i]];
e.cap-=d;
G[e.to][e.rev].cap+=d;
}
}
return cost;
}
}
int main() {
int f;
init(f);
printf("%d\n",-EK_SPFA::min_cost_flow(1,make_crn(n,n)+n*n,f));
return 0;
}好久以前写的,码风都不一样,将就着看吧……
四、拆边
当维护的是有根树的边权时,有一种更为方便的做法——权值下推。
我们可以让每个点维护其与其父亲的这条边的信息。即对于某个点 \(x\),设其父亲节点为 \(f\),从 \(f\) 到 \(x\) 的边权值为 \(w\),那么我们可以直接让 \(x\) 点的点权加上 \(w\)。并且当更改边权 \(w\) 时,可以直接在点 \(x\) 的点权上修改。
特殊的是,当我们查询树上 \(u \to v\) 路径信息时,我们需要减掉 \(lca(u, v)\) 的额外维护的边权,因为 \(lca(u, v)\) 维护的是在它上面的那条边的信息,不是我们需要的路径信息。
过程
对于一条连接 \(u\), \(v\) ,权值为 \(w\) 的有向边 \(e\),我们可以通过新建一个点 \(x\),并将 \(x\) 的点权设为 \(w\),从 \(u \to x\) 和 \(v \to x\) 各连一条有向边。这就是拆边的主要过程。
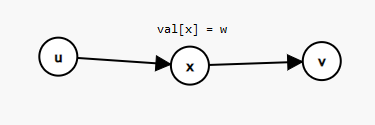
上图说明了拆边的过程。
通过拆边,我们就让维护点权的数据结构可以维护边权。
实例
倍增算法(Kruskal 重构树)
最小生成树是一种针对边权的算法,但是在一些生成树的题中,我们希望能够快速维护边权的信息。那么此时就可以在生成树时直接拆边,已达到我们的目的。这种最小生成树算法被称为 Kruskal 重构树。
Kruskal 重构树执行的过程与最小生成树的 Kruskal 算法类似:
- 将原图的每一个节点看作一棵子树。
- 合并两棵子树时,通过并查集找到它们子树对应的根节点,记作 \(u\), \(v\)。
- 新开一个节点 \(p\),从 \(p\) 分别向 \(u\), \(v\) 两点连边。于是 \(u\) 和 \(v\) 两棵子树就并到了一棵子树,根节点就是 \(p\),并将 \(p\) 点权值赋为 \(u \leftrightarrow v\) 这条边的权值。
在代码上可以如此实现:
const int MaxN = 100000 + 5, MaxV = 200000 + 5;
int N, M;
int cntv = N; // 图中点数
int par[MaxV]; // 并查集(注意大小开为原图两倍)
int val[MaxV]; // 生成树中各点点权
struct edge { int u, v, w; } E[MaxM];
vector<int> Tree[MaxV];
void Kruskal() {
for (int i = 1; i <= N + N - 1; ++i) par[i] = i;
sort(E + 1, E + 1 + M, cmp); // 按权值从小到大排序
for (int i = 1; i <= N; ++i) val[i] = 0;
for (int i = 1; i <= M; ++i) {
int u = E[i].u, v = E[i].v;
int p = Find(u), q = Find(v);
if (p == q) continue;
cntv++;
par[p] = par[q] = cntv;
val[cntv] = E[i].w;
Tree[cntv].push_back(p);
Tree[cntv].push_back(q);
}
}我们可以发现这样建出来的最小生成树(最大生成树同理)有如下性质:
- 原最小生成树上 \(u\) 到 \(v\) 路径上的边权和就是现在 \(u\) 到 \(v\) 路径上的点权和。
- 这是一个大根堆,也是一个二叉堆。
- 原最小生成树上 \(u\) 到 \(v\) 路径上的最大值,就是 \(u\), \(v\) 的最近公共祖先(LCA)的权值。故求最小瓶颈路时,可以使用 Kruskal 重构树的方法。
那么我们就看一道简单的例题:
给定一个 \(n\) 个点,\(m\) 条边的无向图,边上有权值。并有 \(q\) 次询问,每次询问输入两个点 \(u\), \(v\),找出一条路径,使得从 \(u\) 到 \(v\) 路径上的最小值最大,并输出这个最大的最小值;若从 \(u\) 不能到达 \(v\),输出 \(-1\).
使用 Kruskal 重构树算法建出最大生成树后,直接查询 \(u\), \(v\) 两点的 LCA 权值即可。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int MAXN = 10000, MAXM = 50000, MAXQ = 30000;
const int MAXV = 20000, MAXE = 30000, MAXLOG = 20;
int N, M, Q;
int U[MAXM+1], V[MAXM+1], W[MAXM+1];
int lnk[MAXM+1];
int X[MAXQ+1], Y[MAXQ+1], ans[MAXQ+1];
int Head[MAXV+1], To[MAXE+1], Next[MAXE+1];
int fa[MAXV+1][MAXLOG+1], val[MAXV+1], depth[MAXV+1]; // 树的信息
int par[MAXV+1], par2[MAXV+1];
int Head2[MAXV+1], To2[MAXQ*2+1], Next2[MAXQ*2+1], Num[MAXQ*2+1];
bool vis[MAXV+1];
int vs, es, qs;
void init() {
memset(fa, -1, sizeof fa );
memset(depth, -1, sizeof depth );
memset(val, 0x7F, sizeof val );
scanf("%d %d", &N, &M);
for (int i = 1; i <= N * 2; ++i) par[i] = i, par2[i] = i;
for (int i = 1; i <= M; ++i) {
lnk[i] = i;
scanf("%d %d %d", &U[i], &V[i], &W[i]);
}
scanf("%d", &Q);
for (int i = 1; i <= Q; ++i) scanf("%d %d", &X[i], &Y[i]);
}
inline void add_edge(int from, int to) {
es++;
To[es] = to;
Next[es] = Head[from];
Head[from] = es;
}
inline void add_query(int from, int to, int num) {
qs++;
To2[qs] = to;
Num[qs] = num;
Next2[qs] = Head2[from];
Head2[from] = qs;
}
inline bool cmp(int x, int y) { return W[x] > W[y]; }
int Find(int x) { return par[x] == x ? x : par[x] = Find(par[x]); }
int Find2(int x) { return par2[x] == x ? x : par2[x] = Find2(par2[x]); }
// Kruskal 重构树
void Kruskal() {
sort(lnk + 1, lnk + 1 + M, cmp);
vs = N;
for (int I = 1; I <= M; ++I) {
int i = lnk[I], u = U[i], v = V[i], w = W[i];
int p = Find(u), q = Find(v);
if (p != q) {
vs++;
add_edge(vs, p), add_edge(vs, q);
val[vs] = w;
par[p] = par[q] = vs;
}
}
// 处理森林的情况
for (int i = 1; i <= N; ++i) add_edge(0, Find(i));
val[0] = -1;
}
void dfs(int u) {
for (int i = Head[u]; i; i = Next[i]) {
int v = To[i];
if (depth[v] != -1) continue;
depth[v] = depth[u] + 1;
fa[v][0] = u;
for (int j = 1; ( 1 << j ) <= depth[v]; ++j)
fa[v][j] = fa[fa[v][ j - 1 ]][j - 1];
dfs(v);
}
}
void Tarjan(int u) {
for (int i = Head[u]; i; i = Next[i]) {
int v = To[i];
if (vis[v] == true) continue;
Tarjan(v);
par2[v] = u;
vis[v] = true;
}
for (int i = Head2[u]; i; i = Next2[i]) {
int v = To2[i], n = Num[i];
if (vis[v]) ans[n] = Find2(v);
}
}
void solve() {
Kruskal();
depth[0] = 0;
dfs(0);
for (int i = 1; i <= Q; ++i)
add_query(X[i], Y[i], i),
add_query(Y[i], X[i], i);
Tarjan(0);
for ( int i = 1; i <= Q; ++i )
printf("%d\n", val[ans[i]]);
}
int main() {
init();
solve();
return 0;
}LCT 维护最小生成树
还是同一个问题,最小生成树一种边权图,而 LCT 是一种维护点权的数据结构。
老套路,直接拆点。我们可以直接把所有边对应的点建好。然后每次断边时断掉两条边,连边时连上两条边。
再看一道简单的模板题:
有一张 \(n\) 个点,\(m\) 条边的图,边有边权。你需要动态维护两种操作:
- 某一条边消失。
- 询问 \(u\) 到 \(v\) 的最小瓶颈路。
将询问翻转,即从后往前做。然后就变成了动态加边的最小生成树问题,询问时相当于问 \(u\), \(v\) 在最小生成树的路径上最大权值。直接拆点用 LCT 维护即可。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int MaxN = 1000 + 5, MaxM = 100000 + 5, MaxQ = 100000 + 5;
const int MaxV = 101000 + 5;
int N, M, Q;
struct edge { int u, v, w, id; bool ok; } E[MaxM];
int Opt[MaxQ], X[MaxQ], Y[MaxQ];
int Mp[MaxN][MaxN], par[MaxN];
int st[MaxQ], tp;
struct LCT {
#define lson ch[0]
#define rson ch[1]
int fa[MaxV], ch[2][MaxV];
int val[MaxV], maxid[MaxV];
bool rev[MaxV];
inline int getson(int x, int f) { return rson[f] == x; }
inline void reverse(int x) { swap(lson[x], rson[x]); }
inline bool is_root(int x) { return lson[fa[x]] != x && rson[fa[x]] != x; }
inline void update(int x) {
int ls = lson[x], rs = rson[x];
if (val[maxid[ls]] > val[maxid[rs]]) maxid[x] = maxid[ls];
else maxid[x] = maxid[rs];
if (val[x] > val[maxid[x]]) maxid[x] = x;
}
inline void push_down(int x) {
if (rev[x] == true) {
reverse(lson[x]); reverse(rson[x]);
rev[lson[x]] = !rev[lson[x]]; rev[rson[x]] = !rev[rson[x]];
rev[x] = false;
}
}
inline void rotate(int x) {
int f = fa[x], g = fa[f];
int l = getson(x, f);
if (is_root(f) == false) ch[getson(f, g)][g] = x;
if (ch[l ^ 1][x] != 0) fa[ch[l ^ 1][x]] = f;
fa[x] = g; fa[f] = x;
ch[l][f] = ch[l ^ 1][x]; ch[l ^ 1][x] = f;
update(f);
}
void erase_tag(int x) {
if (is_root(x) == false) erase_tag(fa[x]);
push_down(x);
}
inline void splay(int x) {
erase_tag(x);
while (is_root(x) == false) {
int f = fa[x], g = fa[f];
if (is_root(f) == false) {
if (getson(f, g) == getson(x, f)) rotate(f);
else rotate(x);
}
rotate(x);
}
update(x);
}
inline void access(int f) {
int x = 0;
while (f != 0) {
splay(f); rson[f] = x;
update(f);
x = f, f = fa[f];
}
}
inline void make_root(int x) {
access(x); splay(x);
rev[x] = !rev[x]; reverse(x);
}
inline void split(int x, int y) {
make_root(x);
access(y); splay(y);
}
inline void link(int x, int y) {
make_root(x);
fa[x] = y;
}
inline void cut(int x, int y) {
split(x, y);
fa[x] = lson[y] = 0;
update(y);
}
} T;
void init() {
scanf("%d %d %d", &N, &M, &Q);
for (int i = 1; i <= M; ++i) scanf("%d %d %d", &E[i].u, &E[i].v, &E[i].w);
for (int i = 1; i <= Q; ++i) scanf("%d %d %d", &Opt[i], &X[i], &Y[i]);
for (int i = 1; i <= N; ++i) par[i] = i;
}
inline bool cmp(edge x, edge y) { return x.w < y.w; }
int Find(int x) { return x == par[x] ? x : par[x] = Find(par[x]); }
void solve() {
sort(E + 1, E + 1 + M, cmp);
for (int i = 1; i <= M; ++i) {
E[i].ok = true;
E[i].id = i + N;
Mp[E[i].u][E[i].v] = Mp[E[i].v][E[i].u] = i;
T.val[E[i].id] = E[i].w;
}
for (int i = 1; i <= Q; ++i) {
if (Opt[i] == 1) continue;
int e = Mp[X[i]][Y[i]];
E[e].ok = false;
}
for (int i = 1; i <= M; ++i) {
int u = E[i].u, v = E[i].v;
int p = Find(u), q = Find(v);
if (E[i].ok == true && p != q) {
T.link(E[i].id, u); T.link(E[i].id, v);
par[p] = q;
}
}
for (int i = Q; i >= 1; --i) {
int opt = Opt[i], x = X[i], y = Y[i];
if (opt == 1) {
if (x == y) {
st[++tp] = 0;
continue;
}
T.split(x, y);
st[++tp] = T.val[T.maxid[y]];
} else {
int m = Mp[x][y];
T.split(x, y);
int e = T.maxid[y] - N;
if (E[e].w <= E[m].w) continue;
T.cut(E[e].id, E[e].u); T.cut(E[e].id, E[e].v);
T.link(E[m].id, x); T.link(E[m].id, y);
}
}
while (tp > 0) printf("%d\n", st[tp--]);
}
int main() {
init();
solve();
return 0;
}五、总结
拆点和拆边是非常经典的图论技巧之一,而且写起来也非常方便,很容易上手。但缺点在于空间占用需要翻倍,使用时千千万万记得开两倍的数组空间(我才不会告诉你这种东西我写十次 RE 九次)。
\[ \texttt{by Tweetuzki} \ \mathcal{2019.2.23} \]




 京公网安备 11010502036488号
京公网安备 11010502036488号