A Math Problem
时间限制 1s 内存限制 128Mb
求:
ps:[x]表示x向下取整
输入
第一行一个整数T表示测试组数。(0<=T<=10)
第二行一个n和k,n表示序列a的长度。(1<=n,k<=1e6)
第三行n个整数表示ai (0<=ai<=1e6)
输出
每组数据输出题目描述的求和值。
输入样例
2
2 1
3 5
3 2
1 2 3
输出样例
8
2
2
思路:签到题,我们直接暴力求解就行了。
代码如下:
#include<stdio.h>
#include<math.h>
#include<string.h>
int main()
{
int t,n,i;
long long sum,a,k;
scanf("%d",&t);
while(t--)
{
sum=0;
scanf("%d %d",&n,&k);
for(i=0;i<n;i++)
{
scanf("%lld",&a);
sum+=a/k;
}
printf("%lld\n",sum);
}
return 0;
}
C Multivariate function
时间限制 1s 内存限制 512Mb
输入
第一行一个整数T,表示T组测试数据(1 T 10).
每组数据第一行一个整数n (4<=n<=1000).
第二行n个浮点数: x1; x2:::xn; (1<= xi <= 1000000).
输出
输出最大值y,保留三位小数.
输入样例
2
4
1.0 2.0 3.0 4.0
5
1.6 2.6 7.1 2.3 2.6
输出样例
0.167
1.530
样例解释
无
2
思路:由于过于复杂,放弃了。
标准代码:
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 1e3 + 10;
double a[MAXN], b[MAXN];
int main() {
int T, n;
scanf("%d", &T);
while(T--) {
scanf("%d", &n);
for(int i = 1; i <= n; ++i) scanf("%lf", &a[i]);
int p = 0;
for(int i = 3; i <= n - 1; ++i) {
double ans = 0.0;
for(int j = i + 1; j <= n; ++j) {
ans = max(ans, a[i] / a[j]);
}
b[i] = ans;
}
for(int i = n - 2; i >= 3; --i) {
b[i] = max(b[i], b[i + 1]);
}
double y = -1e20;
for(int i = 1; i <= n - 3; ++i) {
for(int j = i + 1; j <= n - 2; ++j) {
y = max(y, (a[j] * b[j + 1] - a[i]) / (a[i] + a[j]));
}
}
printf("%.3lf\n", y);
}
return 0;
}
D Longest Increasing Subsequence
时间限制 1s 内存限制 512Mb
给出一组长度为n的序列,a1; a2; a3; a4; ; ; an, 求出这个序列长度为k的严格递增子序列的个数
输入
第一行输入T组数据T(0<=T <= 10)
第二行输入序列大小n(1 <= n <= 100),长度k(1 <= k <= n)
第三行输入n个数字ai(0 <= ai <= 1e9)
输出
数据规模很大, 答案请对1e9 + 7取模
输入样例
2
3 2
1 2 2
3 2
1 2 3
输出样例
2
3
思路:这个题用动态规划(dp)可以求解
标准代码:
#include <bits/stdc++.h>
using namespace std;
const int MAXN = (int)5e2+10;
const int mod = (int)1e9+7;
int dp[110][110];
int arr[110];
int main() {
int n, k, T;
cin >> T;
while(T--) {
cin >> n >> k;
memset(dp, 0, sizeof dp);
for(int i = 1; i <= n; ++i) {
cin >> arr[i];
dp[i][1] = 1;
}
for(int i = 1; i <= n; ++i) {
for(int j = 2; j <= i; ++j) {
for(int z = 1; z < i; ++z) {
if(arr[z] < arr[i])
dp[i][j] = (dp[i][j]+dp[z][j-1]) % mod;
}
}
}
int ans = 0;
for(int i = 1; i <= n; ++i) {
ans = (ans + dp[i][k]) % mod;
}
cout << ans << endl;
}
return 0;
}
E 玩游戏
时间限制 1s 内存限制 512Mb
zxy和wfy用几堆石子在做游戏。偶数堆石子排成一行,每堆都有正整数颗石子a[i] 。游戏以谁手中的石子最多来决出胜负。石子的总数是奇数,所以没有平局。
zxy和wfy轮流进行,wfy先开始。每回合,玩家从一行的开始或结束处取走整堆石头。这种情况一直持续到没有更多的石子堆为止,此时手中石子最多的玩家获胜。
假设zxy和wfy都发挥出最佳水平,当zxy赢得比赛时输出“zxy”,当wfy赢得比赛时输出“wfy”。
输入
有T组输入,每个输入后有一个n,在n后有n个数字,a1; a2::::an。
n的范围是1 <= n <= 1e5
1 <= a <= 1e5
输出
输出胜利者的名字"zxy"或者"wfy"
输入样例
1
4
5 3 4 5
输出样例
wfy
提示
wfy先开始,只能拿前5 颗或后5 颗石子。
假设他取了前5 颗,这一行就变成了[3,4,5] 。
如果zxy拿走前3 颗,那么剩下的是[4,5],wfy拿走后5 颗赢得10 分。
如果zxy拿走后5 颗,那么剩下的是[3,4],wfy拿走后4 颗赢得9 分。
这表明,取前5 颗石子对wfy来说是一个胜利的举动,所以我们输出wfy 。
思路:这个题目如果做过这种题目的话,应该大概可以推测出来赢的永远是wfy,结果也确实是wfy一直赢,但是我们怎么证明呢?用dp。我们对每一次状态进行结果的推测,如果某种状态能够保证不管zxy如何选,总是wfy赢,那么我们就可以确定wfy一定赢,否则就是zxy赢。
代码如下:
//简易做法
#include<stdio.h>
#include<math.h>
#include<string.h>
#include<algorithm>
using namespace std;
int main()
{
int t,n,a;
scanf("%d",&t);
while(t--)
{
scanf("%d",&n);
for(int i=0;i<n;i++)
scanf("%d",&a);
printf("wfy\n");
}
return 0;
}
F 辞树的肥宅快乐水
时间限制 1s 内存限制 512Mb
题目描述
又到了基情四射的夏天,大家出去约妹子,而肥宅辞树只想宅在机房喝肥宅快乐水。辞树一下子买了n瓶肥宅快乐水。已知他一天里至少喝掉一瓶肥宅水且他是一口干掉一整瓶。(肥宅Orz)
他想要知道自己一共有多少种喝肥宅水的方案。两种方案被认为是不同的,当且仅当辞树买的这些肥宅水能喝的天数不同,或者存在一天两种方案喝的肥宅水瓶数不同。
输入
第一行输入一个正整数T,代表有T组数据(0 < T < 11) 每组数据有一个正整数n,代表辞树买了n瓶肥宅快乐水。(0 < n < 108)
输出
对于每组数据,输出一行,将方案数用二进制表示输出。
输入样例
1
3
输出样例
100
提示
3瓶肥宅快乐水的分配方式如下
1 1 1(三天喝完,一天一瓶)
2 1(两天喝完,第一天两瓶,第二天一瓶)
1 2(两天喝完,第一天一瓶,第二天两瓶)
思路:这个题目如果试几组数据的话就会发现它的结果总是2的次方,结果总是2^(n-1),因此我们只要输入输出就行了,由于这个题目数据非常大,用C/C++是没有办法储存这么大的数字的,所以我们直接考这个捷径就可以了。
代码如下:
#include<stdio.h>
#include<math.h>
#include<string.h>
#include<algorithm>
using namespace std;
int main()
{
int t;
long long x;
scanf("%d",&t);
while(t--)
{
scanf("%lld",&x);
printf("1");
for(int i=1;i<x;i++)
printf("0");
printf("\n");
}
return 0;
}G From The New WorldⅠ
时间限制 1s 内存限制 512Mb
千年之后,「新世界」的孩子们被彻底地控制和管束著,不合适的记忆被消去,被认为有问题的孩子如同不良产品般被处理......
Saki和她的小伙伴们在完人学校迎来了第一个学期考试,考试规则如下:要求你使用自己的咒力对规定的图画进行有限次的念写,你需要找到其中的咒术节点并尽可能的削弱它的咒力值,最后输出最长的咒术节点的长度.
请你用程序的方式来完成考试,可把图画抽象为一段具体的序列,咒术节点可看为特定的数值,特定的数值连续出现越多咒术节点的咒力值越大.每次操作只能将要修改的值修改为自己的咒力值.(即:给定长度为n的序列,用给出的自身咒力值p替换序列中k个数,使规定的数值x连续出现的最长长度最短,输出最终最长的x的连续的长度.保证p! = x)
输入
多组输入,请处理到文件结束
第一行依次输入n; p; x; k. n表示序列的长度,p表示自身咒力值,x表示咒术节点的值,k表示规定修改次数.
(1 <= n <= 100000; 1 <= p <= 20; 0 <= x <= 100000; 0 <= k <= n)
第二行输入n个ai (0 <= ai <= 100000000)表示序列n个元素的值
输出
每行输出咒术节点连续出现最大长度.
输入样例
7 3 5 3
8 2 5 5 5 5 5
输出样例
1
提示
样例解释:修改后的序列为8 2 5 3 3 3 5 最大长度为1
思路:(个人理解,仅供参考!!!)
题目很长,但题意很清晰,我们需要把所有的指定序列缩减的尽可能小。
样例的最长指定序列为5 5 5 5 5 ,长度为5,我们可以修改三次。
第一次,我们修改最中间的,那么他就变成了两个5 5,此时长度就变成了2。
第二次和第三次我们分别把两个5 5变成一个5,此时我们得到了最短的指定序列,因此答案为1.
对这个题目来讲,我们只需要统计所有指定序列的所有长度,然后把最长的分成较短的两节,依次进行k次,得到的最终结果即为答案。
标准代码:
#include <cstdio>
#include <cstring>
#include <cmath>
#include <queue>
#include <algorithm>
using namespace std;
typedef long long LL;
const int INF = 0x3f3f3f3f;
const int MAXN = 1E5+11;
int a[MAXN];
int b[MAXN];
int n,p,x,k,tl;
bool check(int tk){
int cnt = 0;//处理到tk长需要的替换次数
for (int i = 0; i < tl; ++i){
if (b[i] > tk){
cnt += (b[i] - tk)/(tk + 1);
}
}
if (cnt <= k) return true;
return false;
}
int main(){
while (~scanf("%d %d %d %d",&n,&p,&x,&k)){
memset(a,0,sizeof(a));
int cx = 0;
for (int i = 0; i < n; ++i){
scanf("%d",&a[i]);
if (a[i] == x) cx++;
}
if (cx <= k) puts("0");
else{
int tml = 0;int j;
tl = 0;
for (int i = 0; i < n; ){
if (a[i] == x){
j = i; tml = 0;
while (j < n && a[j++] == a[i]){
tml++;
}
b[tl++] = tml; tml = 0; i = j;
}else ++i;
}
int l = 0,r = n;
while (l <= r){
int mid = (l + r)>>1;
if (check(mid)) r = mid - 1;
else l = mid + 1;
}
printf("%d\n",r+1);
}
}
return 0;
}
H 真。签到题
时间限制 1s 内存限制 512Mb
A国的n个作战通信基站大部分被C国的特种部队破坏,基站编号1到n,只剩下编号为a和b的通信基站完好,为了快速恢复通信,A国派出zzx和fk两位工程师去修复,A国的通信基站有一个特殊隐蔽的备用系统,只有让两个完好的通信基站向编号为x的基站发送信号,x是这两个完好基站编号的和或者差的绝对值,该被破坏的基站的备用系统才会被激活,工程师才能恢复被破坏的基站,假设zzx工程师先到达可修复的基站进行修复,接着fk去修复下一个,两人轮流修复,问谁会修复最后一个可修复的基站
输入
输入n,a,b三个整数,代表基站的总数n和剩下的完好的两个基站的编号a,b;
1 < n <= 1e5
1 <= a; b <= n
处理到文件结束
输出
若zzx修复最后一个,输出zzx,否则输出fk
输入样例
5 1 4
10 3 7
输出样例
zzx
fk
思路:这个题思路有点难想,我们首先需要知道能修复的信号基站有多少个。
样例5 1 4中,我们可以修复所有的基站,样例 10 3 7中,我们也可以修复所有的基站。
但是对于10 4 6 这个数据,我们只能修复2 4 6 8 10 这些基站。
从数据上可以按出,能修复的基站个数为n/gcd(a,b),由于总是zzx先修复第一个基站,所以我们只需要判断n/gcd(a,b)的奇偶性就可以得出结果。
代码如下:
#include<stdio.h>
#include<math.h>
#include<string.h>
#include<algorithm>
using namespace std;
int gcd(int a,int b)
{
return b?gcd(b,a%b):a;
}
int main()
{
int n,a,b;
while(~scanf("%d %d %d",&n,&a,&b))
{
int x=gcd(a,b);
if((n/gcd(a,b))%2)
printf("zzx\n");
else
printf("fk\n");
}
return 0;
}I 阶乘之和
时间限制 1s 内存限制 512Mb
对于整数p,给出以下定义
p = x1! + x2! + x3! + ::: + xq!(xi < xjfor all i < j)且xi 6= 0
(注释:p等于多个数的阶乘和,并且x1; x2; x3; :::; xq为不相等的任意正整数,即组成p的阶乘不重复使用)
给定两个整数x,y,判断二者是否能满足以上定义。若二者都满足定义,设x由k1个数的阶乘和组成,y由k2个数的阶乘和组成,若k1 = k2,按下述输出格式输出二者的定义形式(输出时,阶乘按递增形式输出,例如:7=1!+3!)。
输入
第一行输入一个整数T,代表T组测试数据。(1 T 10000)
接下来T行,每行包含两个整数x,y。(1 x; y 1018)
输出
对于每组x,y输出包含两部分:
①如果二者都满足以上定义,输出“SEYES”;如果只有其一满足以上定义,输出“YNEOS”;
如果二者都不满足以上定义,则输出“ONO”。
②当x,y都满足以上定义且k1 = k2时,输出二者的定义形式。否者输出“dWvWb”。
输入样例
4
7 7
1 2
4 2
4 4
输出样例
Case 1:SEYES
7=1!+3!
7=1!+3!
Case 2:SEYES
1=1!
2=2!
Case 3:YNEOS
dWvWb
Case 4:ONO
dWvWb
思路:这个题目如果暴力求解的话是肯定求不出来的,如果我们直接对输入的数据进行拆分,所需要的时间会非常多,而且测试数据也是非常的庞大。因此我们需要找到更好的办法。
分析得知,x,y的值都在1e18的范围内,而18!=6402373705728000(16位),19!=121645100408832000(18位),因此我们只需要对2^18=262144种情况内的所有选择情况进行一次计算,储存结果,等到输入时直接判断结果即可。
代码如下:(代码有些繁琐)
#include<stdio.h>
#include<math.h>
#include<string.h>
#include<algorithm>
#include<map>
using namespace std;
map<long long,int>p,q,num;//三个数组,分别用来 1.标记是否经过匹配存在这个数值 2.储存这个数值的组成信息 3.储存组成数值的数字的个数
long long pow(long long i)
{
long long sum=1;
for(int j=1;j<=i;j++)
sum*=j;
return sum;
}
int main()
{
long long t,i,x,y,j;
long long a[30]={0};
for(i=1;i<=18;i++)//预处理前十八个数字的阶乘
a[i]=pow(i);
for(i=1;i<= 1<<18 ;i++){//进行2^18次查询
long long sum=0,x=0;
for(j=0;j<=18;j++){//对每个i进行位运算,表示是否选择这个数字的阶乘 1为选择,0为不选择
if((i>>j)&1){
sum+=a[j];
x++;
}
if(sum>1e18){//约束条件,x,y小于1e18
p[sum]=1;//标记这个数值存在
q[sum]=i;//储存这个数字的阶乘组成
num[sum]=x;//记录构成这个数值的数字个数
break;
}
if((i>>j)<=0){//如果等于零了,就没有必要进行接下来的位运算
p[sum]=1;
q[sum]=i;
num[sum]=x;
break;
}
}
}
scanf("%lld",&t);
for(int k=1;k<=t;k++){
scanf("%lld %lld",&x,&y);
if(p[x]==1 && p[y]==1){//判断两个数值是否存在
printf("Case %d:SEYES\n",k);
if(num[x]==num[y]){//判断两个的阶乘个数是否一样
printf("%lld=",x);
int ok=0;
for(int j=1;j<=18;j++){
if(q[x]>>j & 1)
{
if(ok==0)
{
printf("%lld!",j);
ok=1;
}
else
printf("+%lld!",j);
}
}
printf("\n%lld=",y);
ok=0;
for(int j=1;j<=18;j++){
if(q[y]>>j & 1)
{
if(ok==0)
{
printf("%lld!",j);
ok=1;
}
else
printf("+%lld!",j);
}
}
printf("\n");
}
else
printf("dWvWb\n");
}
else if(p[x]==1||p[y]==1)
printf("Case %d:YNEOS\ndWvWb\n",k);
else
printf("Case %d:ONO\ndWvWb\n",k);
}
return 0;
}J 过河问题
时间限制 1s 内存限制 65535KB
在漆黑的夜里,N位旅行者来到了一座狭窄而且没有护栏的桥边。如果不借助手电筒的话,大家是无论如何也不敢过桥去的。不幸的是,N个人一共只带了一只手电筒,而桥窄得只够让两个人同时过。如果各自单独过桥的话,N人所需要的时间已知;而如果两人同时过桥,所需要的时间就是走得比较慢的那个人单独行动时所需的时间。问题是,如何设计一个方案,让这N人尽快过桥。
输入
多组数据。
每组测试数据的第一行是一个整数N(从1到1000,包括1和1000)表示共有N个人要过河
每组测试数据的第二行是N个整数Si,表示此人过河所需要花时间。(Si 小于等于100,大于等于1)
输出
输出所有人都过河需要用的最少时间。
输入样例
4
1 2 5 10
输出样例
17
思路:这个题目是一个非常难的题目,样例很多人短时间内根本看不出来是怎么得到的。
对于样例,过程是这样的:
因此,最终结果为2+2+10+1+2=17。
指根据这个我们是做不出来这个题的,但是我们可以从这里面找到一些规律:
对于四个数a,b,x,y(a<=b<=x<=y),我们选择常规做法的话,结果为b+a+x+a+y = 2a+b+x+y;选择上面做法的话结果为b+b+y+a+b=a+3b+y;
两种方案的差值为2a+b+x+y-a-3b-y=a+x-2b;
如果a+x-2b>0即a+x>2b,那么我们就可以选择样例这样的过程,如果不符合,那么我们就用常规做法。
如果最后剩下一个没有过河,那么只有一种方案过河,即b+a+x,因此我们在最后需要判断一下人数的奇偶。
至此,这个题目就解决完了。
代码如下:
#include<stdio.h>
#include<math.h>
#include<string.h>
#include<algorithm>
using namespace std;
bool cmp(int a,int b){
return a>b;
}
int main()
{
int n,t,sum,sum1,min,a[10000],sumx;
while(~scanf("%d",&n))
{
memset(a,0,sizeof(a));
for(int i=0;i<n;i++) scanf("%d",&a[i]);
if(n==1) printf("%d\n",a[0]);
else{
sort(a,a+n,cmp);//降序排列
sum=0;
for(int i=0;i<n-3;i+=2){
if(a[n-2]*2<=(a[n-1]+a[i+1]))//判断是否符合2b<=a+x
sum+=a[n-2]*2+a[i]+a[n-1];
else
sum+=a[i]+a[i+1]+2*a[n-1];
}
if(n&1)//如果是奇数,那么三个数均进行一次加法
sum+=a[n-1]+a[n-2]+a[n-3];
else//如果没有剩余人数,最后两人就一起过河。
sum+=a[n-2];
printf("%d\n",sum);
}
}
return 0;
}



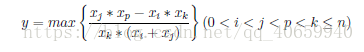
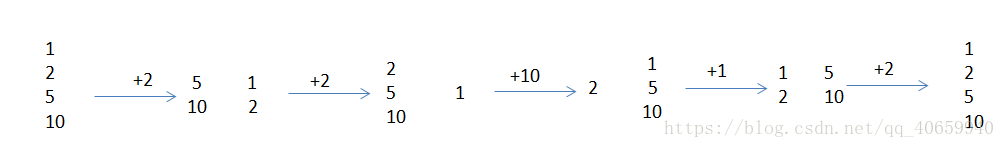

 京公网安备 11010502036488号
京公网安备 11010502036488号