方阵的行列式是一个数字,这个数字包含了矩阵的大量信息。首先,它立即告诉了我们这个矩阵是否可逆。矩阵的行列式为零的话,矩阵就没有逆矩阵。当 A 可逆的时候,其逆矩阵 A−1 的行列式为 1/det(A)。
行列式可以用来求逆矩阵、计算主元和求解方程组,但是我们很少这样做,因为消元会更快。

对于上述矩阵,如果行列式 ad−bc 为零的话,我们不能除以零,也就是没有逆矩阵。其主元为 a 和 d−(c/a)b,主元的乘积就是行列式的值。
行列式有三个基本的性质,由这三个性质我们可以计算任意方针的行列式, A 的行列式记作 det(A) 或者 ∣A∣。
- 性质 1: det I=1,单位矩阵的行列式为 1 ,与之对应的是单位立方体的体积是 1。
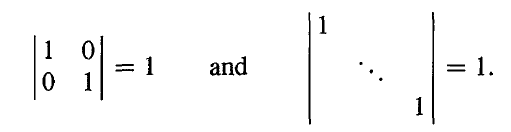
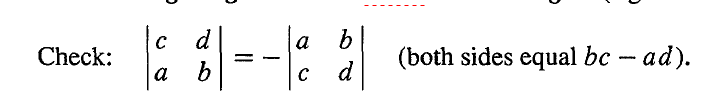
由这个性质,我们可以很容易得到所有置换矩阵的行列式,置换矩阵都是由单位矩阵演化而来,当有奇数次行交换时, det P=−1;当有偶数次行交换时, det P=1。
- 性质 3: 行列式是单独每一行的线性函数(其它行不变)。

若某一行乘以 t,行列式就也乘以 t。如果某一行加上另一行,行列式就也相加。
这不意味着 2I=2det I, 2I 是对其中的每一行都乘以 2,因此要乘以 2n。
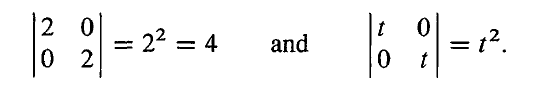
这就像面积或者体积一样,长方形的长和宽都变为原来的 2 倍的话,面积就会变为 4 倍。
- 性质 4: 当矩阵中有两行一样的话, det(A)=0。
利用性质 2,我们对这两行进行行交换,矩阵仍然保持不变,但其行列式需要变号,那么行列式只能为零。
- 性质 5: 用矩阵的一行减去另一行的倍数,行列式不变。
∣∣∣∣ac−λabd−λb∣∣∣∣=∣∣∣∣acbd∣∣∣∣−λ∣∣∣∣aabb∣∣∣∣=∣∣∣∣acbd∣∣∣∣
在消元的过程中,行列式不会改变,如果有行交换的话,符号不同,因此有 det A=±det U。
- 性质 6: 当矩阵的某一行全为零的时候,行列式为零。
利用性质 5,将全零行加上另外一行。
∣∣∣∣a0b0∣∣∣∣=∣∣∣∣aabb∣∣∣∣=0
- 性质 7: 如果矩阵是三角形的,那么行列式等于对角线上元素的乘积。
利用性质 5,我们可以将对角线上面或者下面的元素通过消元法全部变成 0,这不会改变行列式的值。然后,矩阵就只有对角线上有非零值,我们再利用性质 3 将每行的系数提取出来,矩阵就变成了单位矩阵。
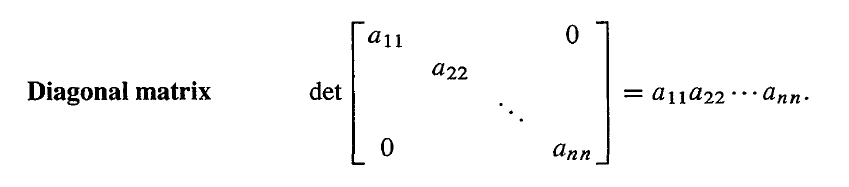
- 性质 8: 如果矩阵是可逆的那么 det(A)̸=0,反之 det(A)=0。
消元过程会让 A 变为 U,如果 A 是不可逆的,那么 U 中一定有全零行,其行列式为零。如果 A 是可逆的,那么 U 中的对角线为主元,其行列式为对角线的乘积,也即主元的乘积。
如果 PA=LU,那么有 ∣P∣ ∣A∣=∣L∣ ∣U∣, L 为对角线上为 1 的下三角矩阵,因此有 det L=1,而 det P=±1,所以 ∣A∣=±∣U∣。
- 性质 9: ∣AB∣=∣A∣∣B∣。
det(AA−1)=det I=1→det A−1=det A1
一个简单的证明过程如下所示:

- 性质 10: 转置矩阵的行列式不变, det AT=det A。
∣P∣ ∣A∣=∣L∣ ∣U∣↔∣PT∣ ∣AT∣=∣LT∣ ∣UT∣
对比以上两项,置换矩阵的逆等于转置,所以有 ∣P∣∣PT∣=1,因此它们同时为 1 或者 -1。对三角矩阵的转置不影响其对角线元素,因此行列式不变,所以有 ∣L∣=∣LT∣,∣U∣=∣UT∣,所以有 ∣A∣=∣AT∣。
因此,任意应用于矩阵的行的性质都可以同时应用到矩阵的列上去。
获取更多精彩,请关注「seniusen」!





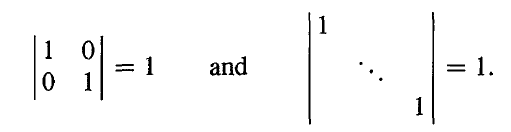
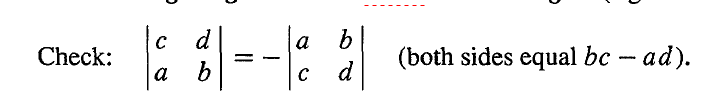

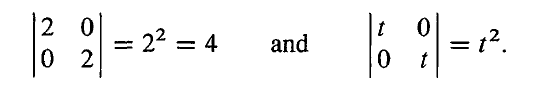
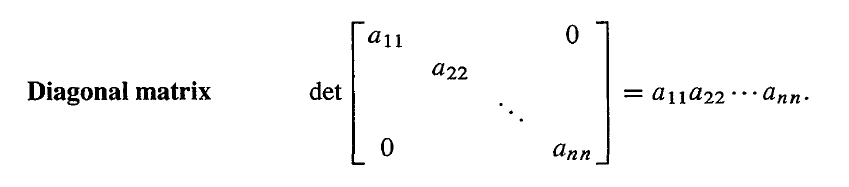



 京公网安备 11010502036488号
京公网安备 11010502036488号