1. 矩阵乘法
如果矩阵 B 的列为 b1,b2,b3,那么 EB 的列就是 Eb1,Eb2,Eb3。
EB=E[b1b2b3]=[Eb1Eb2Eb3]
E (B的第 j 列)=EB 的第 j 列
在消元的过程中,如果遇到了某一行主元的位置为 0,而其下面一行对应的位置不为 0,我们就可以通过行交换来继续进行消元。
如下的矩阵 P23 可以实现将向量或者矩阵的第 2 、 3 行进行交换。
P23=⎣⎡100001010⎦⎤
⎣⎡100001010⎦⎤⎣⎡135⎦⎤=⎣⎡153⎦⎤
⎣⎡100001010⎦⎤⎣⎡200406135⎦⎤=⎣⎡200460153⎦⎤
置换矩阵 Pij 就是将单位矩阵的第 i 行和第 j 行进行互换,当交换矩阵乘以另一个矩阵时,它的作用就是交换那个矩阵的第 i 行和第 j 行。
在消元的过程中,方程两边的系数 A 和 b 都要进行同样的变换,这样,我们可以把 b 作为矩阵 A 的额外的一列,然后,就可以用消元矩阵 E 乘以这个增广的矩阵一次性完成左右两边的变换。
E[A b]=[EA Eb]
⎣⎡1−20010001⎦⎤⎣⎡24−249−3−2−372810⎦⎤=⎣⎡20−241−3−2172410⎦⎤
如果矩阵 A 有 n 列, B 有 n 行,那么我们可以进行矩阵乘法 AB。
假设矩阵 A 有 m 行 n 列,矩阵 B 有 n 行 p 列,那么 AB 是 m 行 p 列的。
(m×n)(n×p)(m×p)[m 行n 列][n 行p 列][m 行p 列]
矩阵乘法的第一种理解方式就是一个一个求取矩阵 AB 位于 (i,j) 处的元素
(AB)ij=A 的第 i 行与 B 的第 j 列的内积=∑aikbkj
第二种理解,矩阵 AB 的列是 A 的列的线性组合
AB=A[b1b2⋯bp]=[Ab1Ab2⋯Abp]
第三种理解,矩阵 AB 的行是 B 的行的线性组合
AB=⎣⎢⎢⎢⎡a1a2⋮am⎦⎥⎥⎥⎤B=⎣⎢⎢⎢⎡a1Ba2B⋮amB⎦⎥⎥⎥⎤
第四种理解,矩阵 AB 是所有 A 的列与 B 的行的乘积的和
AB=[a1a2⋯an]⎣⎢⎢⎢⎡b1b2⋮bn⎦⎥⎥⎥⎤=i=1∑naibi
其中,一列乘以一行称为外积(outer product),(n×1)(1×n)=(n, n),结果为一个 n×n 的矩阵。
⎣⎡234789⎦⎤[1060]=⎣⎡234⎦⎤[16]+⎣⎡789⎦⎤[00]=⎣⎡234121824⎦⎤
结合律: A(BC)=(AB)C
交换律: (A+B)C=AC+BC
交换律: A(B+C)=AB+AC
Ap=p 个 AA⋯A
ApAq=A(p+q)
(Ap)q=Apq
A0=I
矩阵还可以被划分为小块,其中每个小块都是一个更小的矩阵。

如果对矩阵 A 的列的划分和对矩阵 B 的行的划分正好匹配,那么每个块之间就可以进行矩阵乘法。
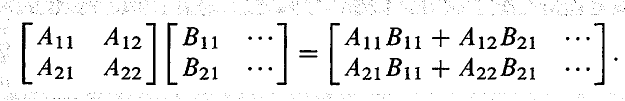
一种特殊的划分就是矩阵 A 的每个小块都是 A 的一列,矩阵 B 的每个小块都是 B 的一行,这种情况就是我们上面说的矩阵相乘的第四种理解。

同样地,在消元的时候,我们也可以按块对系数矩阵进行消元。

2. 矩阵的逆
假设 A 是一个方阵,如果存在一个矩阵 A−1,使得
A−1A=I并且AA−1=I
那么,矩阵 A 就是可逆的, A−1 称为 A 的逆矩阵。
逆矩阵的逆就是进行和原矩阵相反的操作。消元矩阵 E21 的作用是第二个方程减去第一个方程的 2 倍。
E21=⎣⎡1−20010001⎦⎤
其逆矩阵 E21−1 的作用则是第二个方程加上第一个方程的 2 倍。
E21−1=⎣⎡120010001⎦⎤
-
当且仅当在消元过程中产生 n 个主元的时候(允许行交换),矩阵 A 的逆才存在。
-
矩阵 A 不可能有两个不同的逆矩阵,左逆等于右逆。假设 BA=I, AC=I,那么一定有 B=C。
B(AC)=(BA)C→BI=IC→B=C
-
如果矩阵 A 是可逆的,那么 Ax=b 有唯一解 x=A−1b。
-
如果存在一个非零向量 x 使得 Ax=0,那么 A 不可逆,因为没有矩阵可以将零向量变成一个非零向量。
若 A−1 存在,则 x=A−10=0
- 一个 2×2 的矩阵是可逆的,当且仅当 ad−bc 非零。
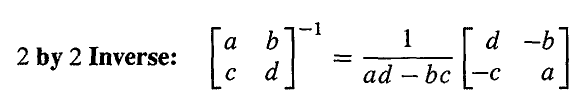
- 一个对角化矩阵如果其对角线上元素非零,那么其有逆矩阵。

如果矩阵 A 和矩阵 B 都是可逆的,那么它们的乘积 AB 也是可逆的。
(AB)−1=B−1A−1
(AB)−1AB=B−1A−1AB=B−1IB=I
同样地,针对三个或更多矩阵的乘积,有
(ABC)−1=C−1B−1A−1
3. 高斯-若尔当消元法(Gauss-Jordan Elimination)求矩阵的逆
我们可以通过消元法来求解矩阵 A 的逆矩阵。思路是这样的,假设 A 是一个 3×3 的矩阵,那么我们可以建立三个方程来分别求出 A−1 的三列。
AA−1=A[x1x2x3]=[e1e2e3]=⎣⎡100010001⎦⎤
Ax1=e1Ax2=e2Ax3=e3
而高斯-若尔当消元法则是一次性求解出这些方程,之前我们求解一个方程的时候,将 b 作为 A 的一列组成增广矩阵,而现在我们则是把 e1、e2、e3 三列一起放入 A 中形成一个增广矩阵,然后进行消元。
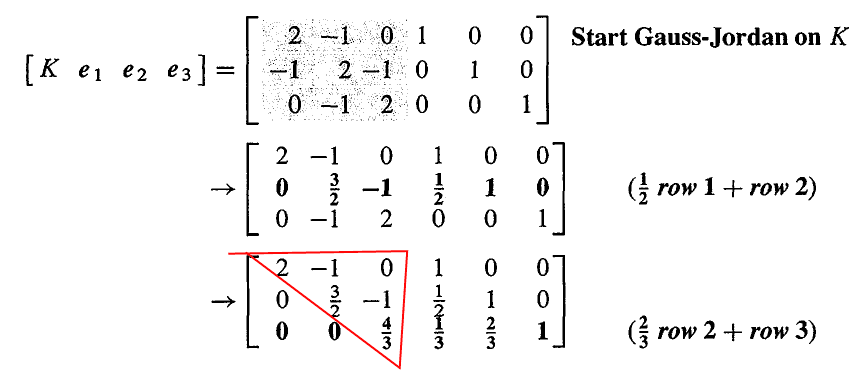
到这里,我们已经得到了一个下三角矩阵 U,高斯就会停在这里然后用回带法求出方程的解,但若尔当将会继续进行消元,直到得到简化阶梯形式(reduced echelon form)。

最后,我们将每行都除以主元得到新的主元都为 1,此时,增广矩阵的前一半矩阵就是 I,而后一半矩阵就是 A−1。

我们用分块矩阵就可以很容易地理解高斯-若尔当消元法,消元的过程就相当于乘以了一个 A−1 将 A 变成了 I,将 I 变成了 A−1。
A−1[AI]=[IA−1]
获取更多精彩,请关注「seniusen」!







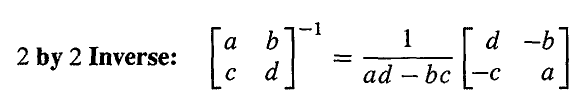






 京公网安备 11010502036488号
京公网安备 11010502036488号