今日小结:今天做了几道分层最短路的题目和几道最小生成树的题目,然后给他们讲了两道题,晚上剩下的时候看了些\(tarjan\),割点那块有点懵。
一. 今日完成的题目:
洛谷P3831,洛谷P4568,洛谷P4822,洛谷P2939,洛谷P1265,洛谷P1318,洛谷P1547,洛谷P4018
二.
1. 当天完成题目数:8道。
2. 未完成6个题目的原因:
3. 复习的知识点:分层最短路,tarjan,最小生成树。
三:
1. 洛谷P3831 回家的路
题目背景
SHOI2012 D2T1
题目描述
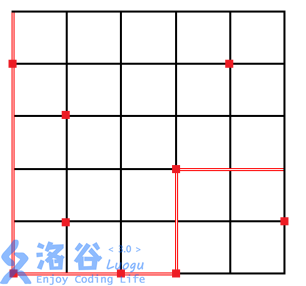
\(2046\) 年 \(OI\) 城的城市轨道交通建设终于全部竣工,由于前期规划周密,建成后的轨道交通网络由\(2n\)条地铁线路构成,组成了一个\(n\)纵\(n\)横的交通网。如下图所示,这\(2n\)条线路每条线路都包含\(n\)个车站,而每个车站都在一组纵横线路的交汇处。
出于建设成本的考虑,并非每个车站都能够进行站内换乘,能够进行站内换乘的地铁站共有\(m\)个,在下图中,标上方块标记的车站为换乘车站。已知地铁运行 \(1\) 站需要 \(2\) 分钟,而站内换乘需要步行 \(1\) 分钟。\(Serenade\) 想要知道,在不中途出站的前提下,他从学校回家最快需要多少时间(等车时间忽略不计)。
输入输出格式
输入格式:
第一行有两个整数\(n,m\)。
接下去\(m\)行每行两个整数\(x,y\),表示第\(x\)条横向线路与第\(y\)条纵向线路的交
汇站是站内换乘站。
接下去一行是四个整数\(x_1,y_1,x_2,y_2\)。表示 \(Serenade\) 从学校回家时,在第 \(x_1\)条横向线路与第\(y_1\)?条纵向线路的交汇站上车,在第\(x_2\)?条横向线路与第\(y_2\)?条纵向线路的交汇站下车。
输出格式:
输出文件只有一行,即 \(Serenade\) 在合理选择线路的情况下,回家所需要的时间。如果 \(Serenade\) 无法在不出站换乘的情况下回家,请输出\(-1\)。
输入输出样例
输入样例#1:
2 1
1 2
1 1 2 2输出样例#1:
5输入样例#2:
6 9
2 1
2 5
3 2
4 4
5 2
5 6
6 1
6 3
6 4
1 1 4 6输出样例#2:
27输入样例#3:
6 10
2 1
2 5
3 2
4 4
5 2
5 6
6 1
6 3
6 4
6 6
1 1 4 6输出样例#3:
26说明
对于 \(30\%\)的数据,\(n\le 50,m\le 1000\);
对于 \(60\%\)的数据,\(n\le 500,m\le 2000\);
对于 \(100\%\)的数据,\(n\le 20000,m\le 100000\);
代码:
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cctype>
#include<queue>
#define maxn 2000001
using namespace std;
int n,m,head[maxn],num,dis[maxn];
inline int qread() {
char c=getchar();int num=0,f=1;
for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
for(;isdigit(c);c=getchar()) num=num*10+c-'0';return num*f;
}
struct edge {
int v,w,nxt;
}e[maxn];
struct node {
int x,y;
bool operator < (const node &a) const {return y>a.y;}
};
struct Edge {
int x,y,id;
}zrj[maxn];
inline void ct(int u, int v, int w) {
e[++num].v=v;
e[num].w=w;
e[num].nxt=head[u];
head[u]=num;
}
inline void ist(int u, int v, int w) {ct(u,v,w);ct(v,u,w);}
inline bool cmp1(Edge a, Edge b) {
if(a.x==b.x) return a.y<b.y;return a.x<b.x;
}
inline bool cmp2(Edge a, Edge b) {
if(a.y==b.y) return a.x<b.x;return a.y<b.y;
}
priority_queue<node>q;
inline void dijkstra() {
memset(dis,0x3f,sizeof(dis));
dis[m+1]=0;q.push((node){m+1,0});
while(!q.empty()) {
int u=q.top().x,d=q.top().y;
q.pop();
if(d!=dis[u]) continue;
for(int i=head[u];i;i=e[i].nxt) {
int v=e[i].v;
if(dis[v]>dis[u]+e[i].w) {
dis[v]=dis[u]+e[i].w;
q.push((node){v,dis[v]});
}
}
}
}
int main() {
n=qread(),m=qread();
for(int i=1;i<=m+2;++i) zrj[i].x=qread(),zrj[i].y=qread(),zrj[i].id=i;
sort(zrj+1,zrj+m+3,cmp1);
for(int i=1;i<m+2;++i)
if(zrj[i].x==zrj[i+1].x)
ist(zrj[i].id,zrj[i+1].id,2*(zrj[i+1].y-zrj[i].y));
sort(zrj+1,zrj+m+3,cmp2);
for(int i=1;i<m+2;++i)
if(zrj[i].y==zrj[i+1].y)
ist(zrj[i].id+m+2,zrj[i+1].id+m+2,2*(zrj[i+1].x-zrj[i].x));
for(int i=1;i<=m;++i) ist(i,i+m+2,1);
ist(m+1,m*2+3,0);ist(m+2,m*2+4,0);
dijkstra();
printf("%d\n",dis[m+2]);
return 0;
}2. 洛谷P4568 飞行路线
题目描述
\(Alice\)和\(Bob\)现在要乘飞机旅行,他们选择了一家相对便宜的航空公司。该航空公司一共在\(n\)个城市设有业务,设这些城市分别标记为\(0\)到\(n−1\),一共有\(m\)种航线,每种航线连接两个城市,并且航线有一定的价格。
\(Alice\)和\(Bob\)现在要从一个城市沿着航线到达另一个城市,途中可以进行转机。航空公司对他们这次旅行也推出优惠,他们可以免费在最多\(k\)种航线上搭乘飞机。那么\(Alice\)和\(Bob\)这次出行最少花费多少?
输入输出格式
输入格式:
数据的第一行有三个整数,\(n,m,k\),分别表示城市数,航线数和免费乘坐次数。
第二行有两个整数,\(s,t\),分别表示他们出行的起点城市编号和终点城市编号。
接下来有\(m\)行,每行三个整数,\(a,b,c\),表示存在一种航线,能从城市\(a\)到达城市\(b\),或从城市\(b\)到达城市\(a\),价格为\(c\)。
输出格式:
只有一行,包含一个整数,为最少花费。
输入输出样例
输入样例#1:
5 6 1
0 4
0 1 5
1 2 5
2 3 5
3 4 5
2 3 3
0 2 100输出样例#1:
8说明
对于\(30\%\)的数据,\(2 \le n \le 50,1 \le m \le 300,k=0\);
对于\(50\%\)的数据,\(2 \le n \le 600,1 \le m \le 6000,0 \le k \le 1\);
对于\(100\%\)的数据,\(2 \le n \le 10000,1 \le m \le 50000,0 \le k \le 10\)
\(2018.12.10\) 增加一组 \(hack\) 数据
思路:一个明显的分层最短路问题,就是建立\(n\)层图,然后建原图的映射边,每个点与它连向的点的映射点距离为\(0\),之后跑\(dijkstra\),因为\(k\)次免费机会可以不用完,所以从\(1\)到\(k\)取最大值就好了。
代码:
#include<cstdio>
#include<cstring>
#include<queue>
#include<algorithm>
#include<cctype>
#define maxn 5000001
using namespace std;
int n,m,k,head[maxn],num,dis[maxn],s,t;
inline int qread() {
char c=getchar();int num=0,f=1;
for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
for(;isdigit(c);c=getchar()) num=num*10+c-'0';return num*f;
}
struct Edge {
int v,w,nxt;
}e[maxn];
struct node {
int x,y;
bool operator < (const node &a) const {return y>a.y;}
};
inline void ct(int u, int v, int w) {
e[++num].v=v;
e[num].w=w;
e[num].nxt=head[u];
head[u]=num;
}
priority_queue<node>q;
inline void dijkstra() {
memset(dis,0x3f,sizeof(dis));
dis[s+n*k]=0;q.push((node){s+n*k,0});
while(!q.empty()) {
int u=q.top().x,d=q.top().y;
q.pop();
if(d!=dis[u]) continue;
for(int i=head[u];i;i=e[i].nxt) {
int v=e[i].v;
if(dis[v]>dis[u]+e[i].w) {
dis[v]=dis[u]+e[i].w;
q.push((node){v,dis[v]});
}
}
}
}
int main() {
n=qread(),m=qread(),k=qread(),s=qread(),t=qread();
for(int i=1,u,v,w;i<=m;++i) {
u=qread(),v=qread(),w=qread();
for(int j=0;j<=k;++j) {
ct(u+j*n,v+j*n,w);
ct(v+j*n,u+j*n,w);
if(j) {
ct(u+j*n,v+(j-1)*n,0);
ct(v+j*n,u+(j-1)*n,0);
}
}
}
dijkstra();
int zrj=0x7fffffff;
for(int i=0;i<=k;++i) zrj=min(zrj,dis[t+i*n]);
printf("%d\n",zrj);
return 0;
}3. 洛谷P4822 冻结
题目描述
“我要成为魔法少女!”
“那么,以灵魂为代价,你希望得到什么?”
“我要将有关魔法和奇迹的一切,封印于卡片之中„„”
在这个愿望被实现以后的世界里,人们享受着魔法卡片(\(SpellCard\),又名符卡)带来的便捷。
现在,不需要立下契约也可以使用魔法了!你还不来试一试?
比如,我们在魔法百科全书(\(Encyclopedia of Spells\))里用“\(freeze\)”作为关键字来查询,会有很多有趣的结果。
例如,我们熟知的\(Cirno\),她的冰冻魔法当然会有对应的 \(SpellCard\) 了。 当然,更加令人惊讶的是,居然有冻结时间的魔法,\(Cirno\) 的冻青蛙比起这些来真是小巫见大巫了。
这说明之前的世界中有很多魔法少女曾许下控制时间的愿望,比如 \(Akemi Homura\)、\(Sakuya Izayoi\)、„„
当然,在本题中我们并不是要来研究历史的,而是研究魔法的应用。
我们考虑最简单的旅行问题吧: 现在这个大陆上有 \(N\) 个城市,\(M\) 条双向的道路。城市编号为 \(1~N\),我们在 \(1\) 号城市,需要到 \(N\) 号城市,怎样才能最快地到达呢?
这不就是最短路问题吗?我们都知道可以用 \(Dijkstra、Bellman-Ford、Floyd-Warshall\)等算法来解决。
现在,我们一共有 K 张可以使时间变慢 \(50\%\)的 \(SpellCard\),也就是说,在通过某条路径时,我们可以选择使用一张卡片,这样,我们通过这一条道路的时间 就可以减少到原先的一半。需要注意的是:
- 在一条道路上最多只能使用一张 \(SpellCard\)。
- 使用一张\(SpellCard\) 只在一条道路上起作用。
你不必使用完所有的 \(SpellCard\)。
给定以上的信息,你的任务是:求出在可以使用这不超过 \(K\) 张时间减速的 \(SpellCard\) 之情形下,从城市\(1\) 到城市\(N\)最少需要多长时间。
输入输出格式
输入格式:
第一行包含三个整数:\(N、M、K\)。
接下来 \(M\) 行,每行包含三个整数:\(A_i、B_i、Time_i\),表示存在一条 \(A_i\)与 \(B_i\)之间的双向道路,在不使用 \(SpellCard\) 之前提下,通过它需要 \(Time_i\)的时间。
输出格式:
输出一个整数,表示从\(1\) 号城市到 \(N\)号城市的最小用时。
输入输出样例
输入样例#1:
4 4 1
1 2 4
4 2 6
1 3 8
3 4 8 输出样例#1:
7说明
样例解释:
在不使用 \(SpellCard\) 时,最短路为 \(1à2à4\),总时间为 \(10\)。现在我们可以使用 \(1\) 次 \(SpellCard\),那么我们将通过 \(2à4\) 这条道路的时间减半,此时总时间为\(7\)。
对于\(100\%\)的数据:\(1 ≤ K ≤ N ≤ 50,M ≤ 1000\)。
\(1≤ A_i,B_i ≤ N,2 ≤ Time_i ≤ 2000\)。
为保证答案为整数,保证所有的 \(Time_i\)均为偶数。
所有数据中的无向图保证无自环、重边,且是连通的。
思路:还是跟其他的分层最短路题目一样,只不过之前的\(k\)次免费的机会变成了\(k\)次免费缩小到一半的机会,那么分层的时候我们把边权由\(0\)改为\(w/2\)就可以了。
代码:
#include<cstdio>
#include<cstring>
#include<queue>
#include<algorithm>
#include<cctype>
#define maxn 5000001
using namespace std;
int n,m,k,head[maxn],num,dis[maxn],s,t;
inline int qread() {
char c=getchar();int num=0,f=1;
for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
for(;isdigit(c);c=getchar()) num=num*10+c-'0';return num*f;
}
struct Edge {
int v,w,nxt;
}e[maxn];
struct node {
int x,y;
bool operator < (const node &a) const {return y>a.y;}
};
inline void ct(int u, int v, int w) {
e[++num].v=v;
e[num].w=w;
e[num].nxt=head[u];
head[u]=num;
}
priority_queue<node>q;
inline void dijkstra() {
memset(dis,0x3f,sizeof(dis));
dis[1+n*k]=0;q.push((node){1+n*k,0});
while(!q.empty()) {
int u=q.top().x,d=q.top().y;
q.pop();
if(d!=dis[u]) continue;
for(int i=head[u];i;i=e[i].nxt) {
int v=e[i].v;
if(dis[v]>dis[u]+e[i].w) {
dis[v]=dis[u]+e[i].w;
q.push((node){v,dis[v]});
}
}
}
}
int main() {
n=qread(),m=qread(),k=qread();
for(int i=1,u,v,w;i<=m;++i) {
u=qread(),v=qread(),w=qread();
for(int j=0;j<=k;++j) {
ct(u+j*n,v+j*n,w);
ct(v+j*n,u+j*n,w);
if(j) {
ct(u+j*n,v+(j-1)*n,w/2);
ct(v+j*n,u+(j-1)*n,w/2);
}
}
}
dijkstra();
int zrj=0x7fffffff;
for(int i=0;i<=k;++i) zrj=min(zrj,dis[n+i*n]);
printf("%d\n",zrj);
return 0;
}4. 洛谷P2939 [USACO09FEB]改造路Revamping Trails
题意翻译
约翰一共有\(N\))个牧场.由\(M\)条布满尘埃的小径连接.小径可 以双向通行.每天早上约翰从牧场\(1\)出发到牧场\(N\)去给奶牛检查身体.
通过每条小径都需要消耗一定的时间.约翰打算升级其中\(K\)条小径,使之成为高 速公路.在高速公路上的通行几乎是瞬间完成的,所以高速公路的通行时间为\(0\).
请帮助约翰决定对哪些小径进行升级,使他每天从\(1\)号牧场到第\(N\)号牧场所花的时间最短
题目描述
Farmer John dutifully checks on the cows every day. He traverses some of the \(M (1 <= M <= 50,000)\) trails conveniently numbered \(1..M\) from pasture \(1\) all the way out to pasture \(N\) (a journey which is always possible for trail maps given in the test data). The \(N\) (\(1 <= N <= 10,000\)) pastures conveniently numbered \(1..N\) on Farmer John's farm are currently connected by bidirectional dirt trails. Each trail i connects pastures \(P1_i\) and \(P2_i\) (\(1 <= P1_i <= N; 1 <= P2_i <= N\)) and requires \(T_i\) (\(1 <= T_i <= 1,000,000\)) units of time to traverse.
He wants to revamp some of the trails on his farm to save time on his long journey. Specifically, he will choose \(K\) (\(1 <= K <= 20\)) trails to turn into highways, which will effectively reduce the trail's traversal time to \(0\). Help FJ decide which trails to revamp to minimize the resulting time of getting from pasture \(1\) to \(N\).
TIME LIMIT: \(2\) seconds
输入输出格式
输入格式:
Line \(1\): Three space-separated integers: \(N, M\), and \(K\)
Lines \(2..M+1\): Line \(i+1\) describes trail i with three space-separated integers: \(P1_i, P2_i\), and \(T_i\)
输出格式:
- Line \(1\): The length of the shortest path after revamping no more than \(K\) edges
输入输出样例
输入样例#1:
4 4 1
1 2 10
2 4 10
1 3 1
3 4 100 输出样例#1:
1 说明
\(K\) is \(1\); revamp trail \(3->4\) to take time \(0\) instead of \(100\). The new shortest path is \(1->3->4\), total traversal time now \(1\).
思路:依旧是分层最短路,这次的分层最短是的\(k\)是有\(k\)次可以不花费任何代价去走一条路,那么我们把图分为\(n\)层,每条边连向映射点与原来边的起来的距离为\(0\),然后跑\(dijkstra\),就做完了。
代码:
#include<cstdio>
#include<cstring>
#include<queue>
#include<algorithm>
#include<cctype>
#define maxn 5000001
using namespace std;
int n,m,k,head[maxn],num,dis[maxn],s,t;
inline int qread() {
char c=getchar();int num=0,f=1;
for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
for(;isdigit(c);c=getchar()) num=num*10+c-'0';return num*f;
}
struct Edge {
int v,w,nxt;
}e[maxn];
struct node {
int x,y;
bool operator < (const node &a) const {return y>a.y;}
};
inline void ct(int u, int v, int w) {
e[++num].v=v;
e[num].w=w;
e[num].nxt=head[u];
head[u]=num;
}
priority_queue<node>q;
inline void dijkstra() {
memset(dis,0x3f,sizeof(dis));
dis[1+n*k]=0;q.push((node){1+n*k,0});
while(!q.empty()) {
int u=q.top().x,d=q.top().y;
q.pop();
if(d!=dis[u]) continue;
for(int i=head[u];i;i=e[i].nxt) {
int v=e[i].v;
if(dis[v]>dis[u]+e[i].w) {
dis[v]=dis[u]+e[i].w;
q.push((node){v,dis[v]});
}
}
}
}
int main() {
n=qread(),m=qread(),k=qread();
for(int i=1,u,v,w;i<=m;++i) {
u=qread(),v=qread(),w=qread();
for(int j=0;j<=k;++j) {
ct(u+j*n,v+j*n,w);
ct(v+j*n,u+j*n,w);
if(j) {
ct(u+j*n,v+(j-1)*n,0);
ct(v+j*n,u+(j-1)*n,0);
}
}
}
dijkstra();
int zrj=0x7fffffff;
for(int i=0;i<=k;++i) zrj=min(zrj,dis[n+i*n]);
printf("%d\n",zrj);
return 0;
}5. 洛谷P1265 公路修建
题目描述
某国有\(n\)个城市,它们互相之间没有公路相通,因此交通十分不便。为解决这一“行路难”的问题,政府决定修建公路。修建公路的任务由各城市共同完成。
修建工程分若干轮完成。在每一轮中,每个城市选择一个与它最近的城市,申请修建通往该城市的公路。政府负责审批这些申请以决定是否同意修建。
政府审批的规则如下:
\((1)\)如果两个或以上城市申请修建同一条公路,则让它们共同修建;
\((2)\)如果三个或以上的城市申请修建的公路成环。如下图,\(A\)申请修建公路\(AB\),\(B\)申请修建公路\(BC\),\(C\)申请修建公路\(CA\)。则政府将否决其中最短的一条公路的修建申请;

\((3)\)其他情况的申请一律同意。
一轮修建结束后,可能会有若干城市可以通过公路直接或间接相连。这些可以互相:连通的城市即组成“城市联盟”。在下一轮修建中,每个“城市联盟”将被看作一个城市,发挥一个城市的作用。
当所有城市被组合成一个“城市联盟”时,修建工程也就完成了。
你的任务是根据城市的分布和前面讲到的规则,计算出将要修建的公路总长度。
输入输出格式
输入格式:
第一行一个整数\(n\),表示城市的数量。(\(n≤5000\))
以下\(n\)行,每行两个整数\(x\)和\(y\),表示一个城市的坐标。(\(-1000000≤x,y≤1000000\))
输出格式:
一个实数,四舍五入保留两位小数,表示公路总长。(保证有惟一解)
输入输出样例
输入样例#1:
4
0 0
1 2
-1 2
0 4输出样例#1:
6.47说明
修建的公路如图所示: 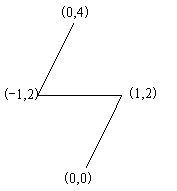
思路:第一眼,我们思路是对每两个点求出它们之间的距离,然后建边,跑\(Kruskal\),但是看了数据范围后放弃了,因为\(m\)太大,不能用\(Kruskal\),于是就用\(prim\),但是数组好像又开不下,那就干脆从\(1\)开始扩展,先\(O(n)\)处理出\(1\)号点到其它所有点的距离,然后再跑\(prim\),因为保证一定有解,跑完之间输出答案就行了。
代码:
#include<cstdio>
#include<cstring>
#include<cmath>
#define maxn 5007
#define dl double
using namespace std;
int n,m,x[maxn],y[maxn];
dl dis[maxn],ans,minn,num;
bool vis[maxn];
inline dl jl(int i,int j) {
return sqrt((double)(x[i]-x[j])*(x[i]-x[j])+(double)(y[i]-y[j])*(y[i]-y[j]));
}
int main() {
scanf("%d",&n);
for(int i=1;i<=n;++i) scanf("%d%d",&x[i],&y[i]);
for(int i=2;i<=n;++i) dis[i]=jl(1,i);
dis[1]=0,vis[1]=1;
for(int i=1;i<n;++i) {
minn=1e9;
int k=0;
for(int j=1;j<=n;++j) if(!vis[j]&&minn>dis[j]) minn=dis[j],k=j;
vis[k]=1,ans+=minn;
for(int j=1;j<=n;++j) {
num=jl(k,j);
if(!vis[j]&&dis[j]>num) dis[j]=num;
}
}
printf("%0.2lf",ans);
return 0;
}6. 洛谷P1318 积水面积
题目描述
一组正整数,分别表示由正方体叠起的柱子的高度。若某高度值为\(x\),表示由\(x\)个正立方的方块迭起(如下图,\(0<=x<=5000\))。找出所有可能积水的地方(图中蓝色部分),统计它们可能积水的面积总和(计算的是图中的横截面积。一个立方体的位置,为一个单位面积)。
如图:柱子高度变化为 0 1 0 2 1 2 0 0 2 0
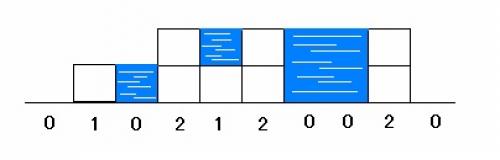
图中蓝色部分为积水面积,共有\(6\)个单位面积积水。
输入输出格式
输入格式:
两行,第一行n,表示有n个数(\(3<=n<=10000\))。第2行连续n个数表示依次由正方体迭起的高度,保证首尾为\(0\)。
输出格式:
一个数,可能积水的面积。
输入输出样例
输入样例#1:
10
0 1 0 2 1 2 0 0 2 0输出样例#1:
6思路:挺水的一道题,但是第一遍写还是错了,我以为是今年noip T1,然而想错了,没认真读题,这个题其实就是看看一个位置的左右高度有不有差值,有的话就加上这个差值。
代码:
#include<iostream>
#include<cstdio>
#define maxn 10001
using namespace std;
int n,l[maxn],r[maxn],a[maxn],ans;
int main() {
scanf("%d",&n);
for(int i=1;i<=n;++i) {
scanf("%d",&a[i]);
l[i]=max(l[i-1],a[i]);
}
for(int i=n;i>=1;--i) r[i]=max(r[i+1],a[i]);
for(int i=1;i<=n;++i)
if(min(l[i],r[i])-a[i]>0) ans+=min(l[i],r[i])-a[i];
printf("%d\n",ans);
return 0;
}7. 洛谷P1547 Out of Hay
题目背景
奶牛爱干草
题目描述
\(Bessie\) 计划调查\(N (2 <= N <= 2,000)\)个农场的干草情况,它从\(1\)号农场出发。农场之间总共有M \((1 <= M <= 10,000)\)条双向道路,所有道路的总长度不超过\(1,000,000,000\)。有些农场之间存在着多条道路,所有的农场之间都是连通的。
\(Bessie\)希望计算出该图中最小生成树中的最长边的长度。
输入输出格式
输入格式:
两个整数\(N\)和\(M\)。
接下来\(M\)行,每行三个用空格隔开的整数\(A_i, B_i\)和\(L_i\),表示\(A_i\)和 \(B_i\)之间有一条道路长度为\(L_i\)。
输出格式:
一个整数,表示最小生成树中的最长边的长度。
输入输出样例
输入样例#1:
3 3
1 2 23
2 3 1000
1 3 43输出样例#1:
43思路:用来练最小生成树的,可以说是一道比较水的题目,可以直接跑\(Kruskal\),并且每次向MST中加一条边时就更新最大值,最后输出最大值。然后……就做完了。
代码:
#include<algorithm>
#include<cstdio>
#define maxn 10001
using namespace std;
int n,maxx,k,m,fa[2001];
struct node {
int u,v,w;
}e[maxn];
inline bool cmp(node a, node b) {return a.w<b.w;}
inline int find(int x) {return fa[x]==x?x:fa[x]=find(fa[x]);}
inline void uni(int x,int y) {x=find(x),y=find(y);fa[y]=x;}
int main() {
scanf("%d%d",&n,&m);
for(int i=1;i<=m;++i) scanf("%d%d%d",&e[i].u,&e[i].v,&e[i].w);
sort(e+1,e+1+m,cmp);
for(int i=1;i<=n;++i) fa[i]=i;
for(int i=1;i<=m;++i) {
if(find(e[i].u)!=find(e[i].v)) {
maxx=max(maxx,e[i].w);
uni(e[i].u,e[i].v);
k++;
}
if(k==n-1) break;
}
printf("%d\n",maxx);
return 0;
}8. 洛谷P4018 Roy&October之取石子
题目背景
\(Roy\)和\(October\)两人在玩一个取石子的游戏。
题目描述
游戏规则是这样的:共有\(n\)个石子,两人每次都只能取\(p^k\)个(\(p\)为质数,\(k\)为自然数,且\(p^k\)小于等于当前剩余石子数),谁取走最后一个石子,谁就赢了。
现在\(October\)先取,问她有没有必胜策略。
若她有必胜策略,输出一行"\(October wins!\)";否则输出一行"\(Roy wins!\)"。
输入输出格式
输入格式:
第一行一个正整数T,表示测试点组数。
第\(2\)行~第\((T+1)\)行,一行一个正整数\(n\),表示石子个数。
输出格式:
\(T\)行,每行分别为"\(October wins!\)"或"\(Roy wins!\)"。
输入输出样例
输入样例#1:
3
4
9
14输出样例#1:
October wins!
October wins!
October wins!说明
对于\(30\%\)的数据,\(1<=n<=30\);
对于\(60\%\)的数据,\(1<=n<=1,000,000\);
对于\(100\%\)的数据,\(1<=n<=50,000,000,1<=T<=100,000\)。
(改编题)
思路:被洛谷标签给骗了,不知道为什么这道题的标签是\(prim\),本来是想练最小生成树,看数据范围,根本不可做,而且……也没法建边啊,洛谷标签真的是……不过点进来了,就做做吧,发现这其实就是个打表题,如果输入的\(n\)模\(6\)值为\(0\),就是先手必败态,否则为先手必胜态。
代码:
#include<cstdio>
using namespace std;
int t,n;
int main() {
scanf("%d",&t);
while(t--) {
scanf("%d",&n);
if(n%6) printf("October wins!\n");
else printf("Roy wins!\n");
}
return 0;
}



 京公网安备 11010502036488号
京公网安备 11010502036488号