目录
1.小红的环形字符串
题目描述
小红拿到了一个环形字符串s。所谓环形字符串,指首尾相接的字符串。
小红想顺时针截取其中一段连续子串正好等于t,一共有多少种截法?
输入描述:
第一行输入字符串 s。 第二行输入字符串 t。 1≤len(t)≤len(s)≤1000
输出描述:
环形字符串 s 截取一段连续子串等于字符串 t 的方案数。
示例1
输入
ababab aba
输出
3
说明
由于首尾相连,所以有3种截法,如下图:
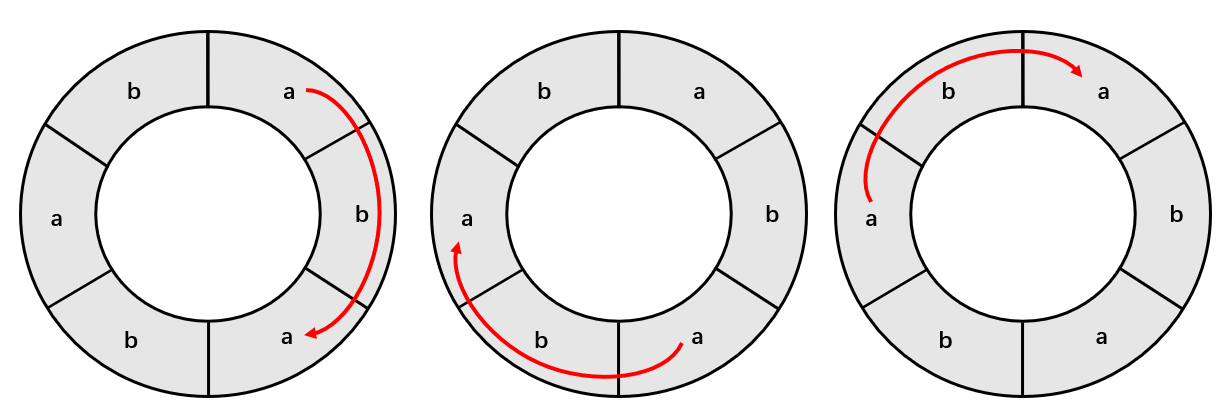
思路
定义一个字符串为原字符串遍历两次,例如输入abc,定义一个字符串为abcabc,利用string的substr方法
代码
#include <iostream>
#include <cstdio>
using namespace std;
int main()
{
string ss, t, s;
int ans = 0;
cin >> ss >> t;
s = ss + ss;
int len = ss.length();
int lent = t.length();
for (int i = 0; i < len; i++) {
if (s.substr(i, lent) == t) {
ans++;
}
}
cout << ans << endl;
return 0;
}2.相邻不同数字的标记
题目描述
小红拿到了一个数组,每个数字被染成了红色或蓝色。
小红有很多次操作,每次操作可以选择两个相邻的不同颜色的数字标记,并获得它们数字之和的得分。已经被标记的数字无法再次标记。
小红想知道,自己最多能获得多少分。
输入描述:
第一行输入一个正整数 n ,代表数组的长度。 第二行输入 n 个正整数 ai,代表小红拿到的数组。
第三行输入一个仅包含 'R' 和 'B' 的字符串,第 iii 个字符为 'R' 代表数组第 i 个数被染成红***'代表被染成蓝色。
1≤n≤10^5
1≤ai≤10^9
输出描述:
输出一个整数,表示小红最多能获得的分值。
示例1
输入
5 1 3 2 6 5 BRRBB
输出
12
说明
第一次选择标记第一个数和第二个数,标记的数是1和3。 第二次选择标记第三个数和第四个数,标记的数是2和6。 总得分为1+3+2+6=12
思路
这是一道经典的dp问题,当前的选择会影响下一步的选择(比如字符串RBR,B与两个R均相邻,但选择第一个R后无法选择第二个R,) 考虑用动态规划
dp[i]表示1~i个数字所得到的最大分数,每次判断时先继承dp[i-1],在i和i-1颜色不同时
①不选 i, dp [ i ] = dp [ i - 1 ]
②选i , dp [ i ] = dp [ i - 2 ] + a [ i ] + a [ i - 1]
取两者中大的
dp[i] = max(dp[i - 1], dp[i - 2] + a[i] + a[i - 1]);
代码
#include <iostream>
#include <cstdio>
using namespace std;
typedef long long ll;
ll n, a[200010], ans;
bool st[200010];
char s[200010];
ll dp[200010];
int main()
{
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> a[i];
}
cin >> s + 1;
for (int i = 2; i <= n; i++) {
dp[i] = dp[i - 1];
if (s[i] != s[i - 1]) {
dp[i] = max(dp[i - 1], dp[i - 2] + a[i] + a[i - 1]);
}
}
cout << dp[n] << endl;
return 0;
}3.小红的俄罗斯方块
题目描述
小红正在玩一个奇怪的俄罗斯方块游戏。已知这个俄罗斯方块只有以下一种图形:
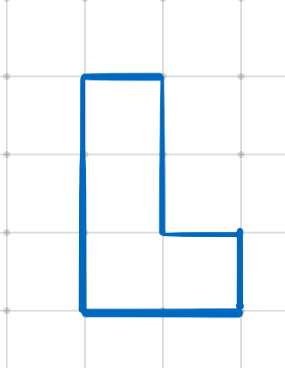
这个图形可以顺时针不旋转,旋转90度、180度、270度,分别变成以下四种情况:
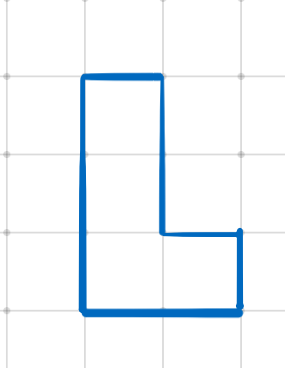

当图形无法下落的时候,会停住不动。
请注意,这个俄罗斯方块没有消除的情况。也就是说会越累积越高。
假设游戏共有 8 列,高度是无限的。请你输出最终每一列的高度。
输入描述:
第一行输入方块的数量 n。 接下来的 n 行,每行输入两个正整数 a 和 b,分别代表方块旋转的角度以及从哪一列下落的。方块是顺序下落的,也就是说前一个方块落到底之前,后一个方块不会开始下落。 1≤n≤100 a 一定是 0、90、180、270四个中的一个,b 代表方块的左端那一列,保证右端不会超过8。也就是说,若 a为0或180,1≤b≤7若a为 90或270,1≤b≤6
输出描述:
输出 8 个正整数,分别代表最终8列的高度。
示例1
输入
3 0 1 90 2 180 4
输出
3 3 3 4 4 0 0 0
说明
第一个方块下落后,地图变成了这样:
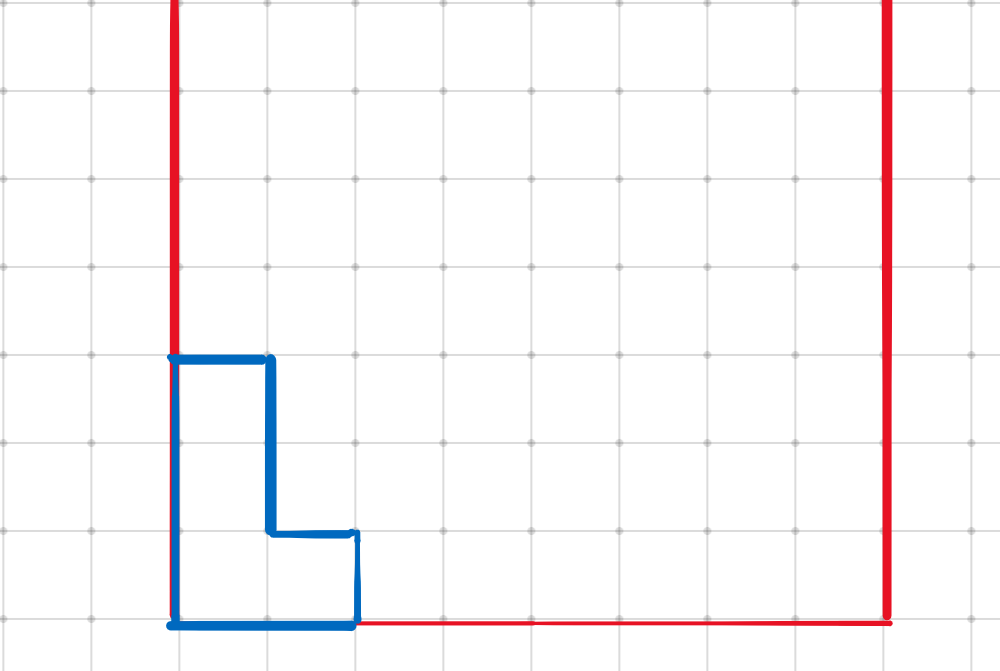
第二个方块下落后,地图变成了这样:
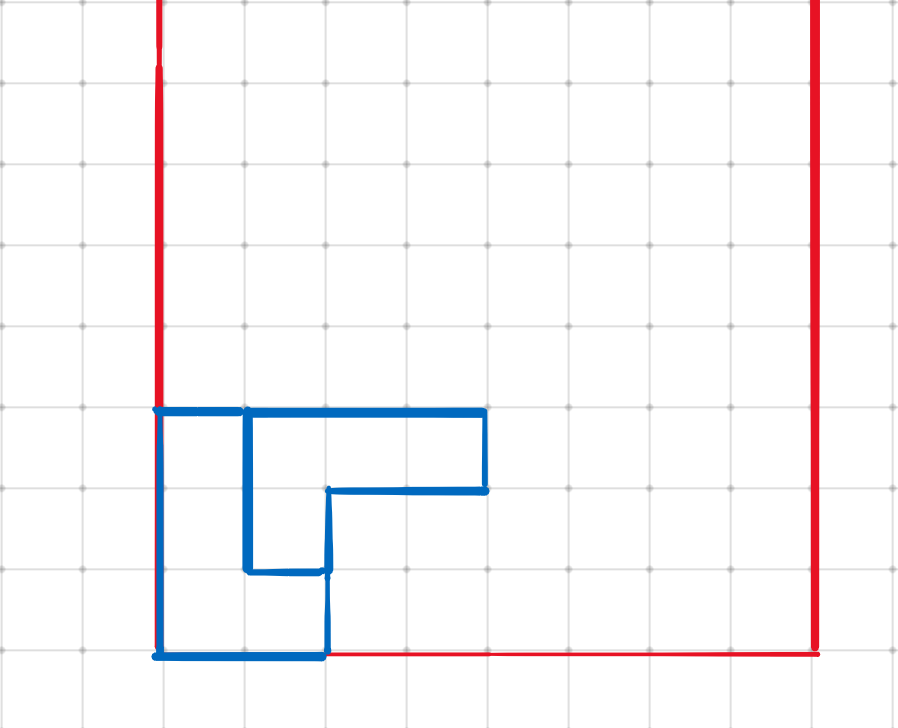
第三个方块下落后,地图变成了这样:
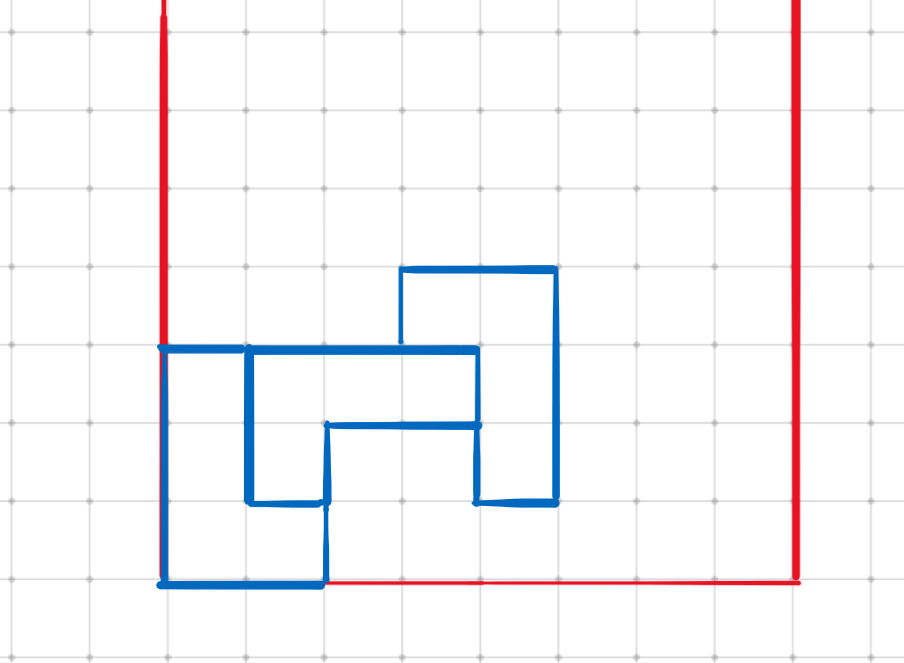
最终,8列的高度为:3 3 3 4 4 0 0 0
思路
简单的模拟问题
代码
#include <iostream>
#include <cstdio>
using namespace std;
typedef long long ll;
ll n;
ll a, b;
ll h[10];
int main()
{
cin >> n;
for (int i = 0; i < n; i++) {
cin >> a >> b;
if (a == 0) {
ll base = max(h[b], h[b + 1]);
h[b] = base + 3;
h[b + 1] = base + 1;
}
else if (a == 90) {
int base = max(max(h[b], h[b + 1] - 1), h[b + 2] - 1);
h[b] = base + 2;
h[b + 1] = base + 2;
h[b + 2] = base + 2;
}
else if (a == 180) {
int base = max(h[b] - 2, h[b + 1]);
h[b] = base + 3;
h[b + 1] = base + 3;
}
else if (a == 270) {
int base = max(max(h[b], h[b + 1]), h[b + 2]);
h[b] = base + 1;
h[b + 1] = base + 1;
h[b + 2] = base + 2;
}
}
for (int i = 1; i <= 8; i++) {
cout << h[i] << " ";
}
return 0;
}4.小红打怪
题目描述
已知地图上有 n 只怪物,每只怪物的血量是 ai,攻击力是 bi。小红准备去地图上探险杀怪,她的初始血量为 h。
小红有两个技能:
1. 普通攻击:对一只怪物造成1点伤害。
2. 强力攻击:对一只怪物造成2点伤害。
但是强力攻击是有冷却时间的。释放一个强力攻击后,需要2回合冷却(即释放2次普通攻击后)才能再次释放。
小红每次攻击后,若怪物没有死亡(即血量大于0),小红都会承受一次怪物攻击力的伤害。但是小红可以在战斗开始前喝血药,每个血药可以回复 k 点血量。也就算说, x 瓶血药可以将小红的初始血量提高到 h+x∗k
已知每只怪物都是不可复活的,当小红血量为0或负数时死亡。小红选择打一个怪时,在该怪物被打死之前不会更换目标。
当小红打死一只怪物去寻找另外一只怪物的过程中,我们可以认为强力攻击的冷却已经恢复完毕。
请问,小红初始带了 x 瓶血药时,最多可以击杀多少只怪物?
上述问题会重复 q次,每次询问都是独立的,小红初始的血瓶数量可能不同。
输入描述:
第一行输入三个正整数 n,h,k,代表地图上怪物的数量、小红的初始血量,以及小红每瓶血药可以回复的血量。 接下来的 n 行,每行输入两个正整数 ai 和 bi,代表地图上每只怪物的血量和攻击力。 接下来的一行输入一个正整数 q,代表询问次数。 接下来的一行,输入 q 个正整数 x,代表每次询问中小红携带的血药数量。 1≤n,q,h,k,ai,bi,x≤10^5
输出描述:
输出一行 q 个正整数,代表小红携带 x 瓶血药时能击杀的最多怪物数量。
示例1
输入
3 1 2 5 1 5 2 3 2 3 1 2 3
输出
1 1 2
说明
第一只怪物小红需要攻击4次才能杀死,所以会被怪物打3下,掉血为1*3=3。 第二只怪物小红需要攻击4次才能杀死,所以会被怪物打3下,掉血为2*3=6。 第三只怪物小红需要攻击2次才能杀死,所以会被怪物打1下,掉血为2*1=2。 当小红携带1瓶血药时,可以先将血量回复至3点,然后击杀第三只怪物,剩余血量为1。 当小红携带2瓶血药时,无法击杀两只怪物。 当小红携带3瓶血药时,可以击杀第一只、第三只怪物。
思路
考察前缀和和二分,此处二分利用了algorithm包下的lower_bound函数,可以得到数组中大于等于一个值的最小下标
用c数组记录每一只怪物需要攻击几次才能杀死,d数组记录每个怪物会让小红掉多少滴血,对d数组从小到大排序,再对d数组进行前缀和,最后利用二分函数计算最多杀敌数量
代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long ll;
ll n, h, k;//怪物的数量,小红的初始血量,小红每瓶血药可以回复的血量
ll a[100010], b[100010];//怪物的血量和攻击力
ll q, x;
int l[100010];
ll s[100010];
int p;
ll ans;
ll c[100010], d[100010];
ll gong(ll i) {
return lower_bound(s, s + 100010, i) - s + 1;
}
int main()
{
for (int i = 0; i < 100010; i++) {
if (p % 3 == 0) {
l[i] = 2;
}
else if (p % 3 == 1) {
l[i] = 1;
}
else if (p % 3 == 2) {
l[i] = 1;
}
p++;
}
s[0] = 2;
for (int i = 1; i < 100010; i++) {
s[i] += s[i - 1] + l[i];
}
cin >> n >> h >> k;
for (int i = 0; i < n; i++) {
cin >> a[i] >> b[i];
c[i] = gong(a[i]);
d[i] = (c[i] - 1) * b[i];
}
cin >> q;
sort(d, d + n);
for (int i = 1; i < n; i++) {
d[i] += d[i - 1];
}
for (int i = 0; i < q; i++) {
cin >> x;
int pp = lower_bound(d, d + n, h + k * x) - d;
cout << pp << " ";
}
return 0;
}



 京公网安备 11010502036488号
京公网安备 11010502036488号