描述
题目描述
首先给我们一个可爱的小青蛙, 一次可以上一级台阶, 一次可以上两级台阶
然后给了我们要到的台阶的数, 问我们最后可以有多少种跳法
样例解释
样例输入
2
这个很是显而易见, 可以跳两次个台阶, 也是可以一次跳两个台阶
所以我们的样例输出是
2
题解
解法一: 裸的动态规划
实现思路
我们可以发现这么一个事情, 就是在当前楼梯, 我们可以发现, 我们是可以从前一个楼梯或者前两个楼梯转移过来
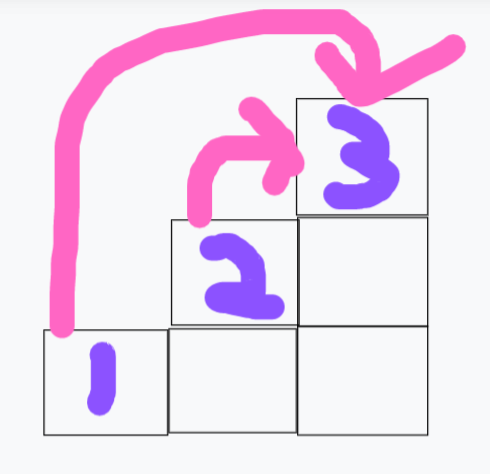
就如图所示, 我们第三层楼梯, 可以从我们的第二层楼梯上去, 同时也是可以从我们的第一层楼梯上去
所以我们可以很容易的得到我们的状态转移方程
当的时候,
当的时候
代码实现
class Solution {
public:
int jumpFloor(int number) {
vector<int> dp(number + 1, 0);
// 我们的dp数组
dp[1] = 1, dp[2] = 2;
// 初始化,就是我们一个台阶的时候是1步,两个台阶的时候是两步
for (int i = 3; i <= number; i++) dp[i] = dp[i - 1] + dp[i - 2];
// 我们根据我们的递推关系求取出来我们的答案
return dp[number];
// 返回我们最后的答案
}
};
时空复杂度分析
时间复杂度:
理由如下: 我们进行了一个长度为的递推
空间复杂度:
理由如下: 我们开辟了一个大小为的数组
解法二: 状态压缩的动态规划
实现思路
其实我们可以很容易的发现, 我们的每一个状态其实只与我们的前两个状态有关系, 所以我们可以采用滚动数组的一个思想去优化我们的这个空间,我们直接省去了整个数组,对每一位,假设这一位是只保留
代码实现
class Solution {
public:
int jumpFloor(int number) {
if (number == 1 || number == 2) return number;
// 特殊情况单独判断
int a = 1, b = 2, res = 0;
// 滚动数组
for (int i = 3; i <= number; i++) {
res = a + b;
a = b, b = res;
}
// 每次判断的时候同时交换值
return res;
}
};
时空复杂度分析
时间复杂度:
理由如下: 我们直接递推即可
空间复杂度:
理由如下: 我们只是开辟了常数级别的一个空间






 京公网安备 11010502036488号
京公网安备 11010502036488号