Description：

There is a slope on the 2D plane. The lowest point of the slope is at the origin. There is a small ball falling down above the slope. Your task is to find how many times the ball has been bounced on the slope.

It’s guarantee that the ball will not reach the slope or ground or Y-axis with a distance of less than 1 from the origin. And the ball is elastic collision without energy loss. Gravity acceleration g=9.8m/s2.
这里写图片描述

Input

There are multiple test cases. The first line of input contains an integer T (1 ≤ T ≤ 100), indicating the number of test cases.

The first line of each test case contains four integers a, b, x, y (1 ≤ a, b, -x, y ≤ 100), indicate that the slope will pass through the point(-a, b), the initial position of the ball is (x, y).

Output

Output the answer.

It’s guarantee that the answer will not exceed 50.

Sample Input

1
5 1 -5 3

Sample Output

2

这道题考的其实是物理知识，而且是高中物理知识，仿佛又想起了当年备战高考的岁月。。。
而且好长时间不碰力学这一块了，公式啥的已经忘光了，好不容易才想起来的，也许高中生更适合做这道题吧。。

这道题说一个小球从斜面上方自由落体，斜面右边是地面，问小球可以在斜面上弹几次，也就是一共碰斜面几次，小球是完全弹性碰撞，不损失能量·。

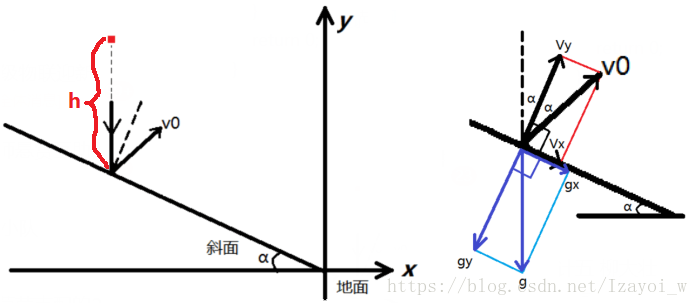
我们可以把速度和重力加速度按平行于斜面和垂直于斜面的方向分解：
这里写图片描述

这样每一次从斜面上弹起到再度落到斜面上，对于垂直于斜面的方向来说，初速度为Vy，加速度为gy，是一个竖直上抛再落回原处的模型，所以由此得知，每一次小球从斜面上弹起到落在斜面上，需要的时间t是一样的，我们列动量定理求t：
m gy t = m Vy - (- m Vy) ，解出 t = 2 Vy / gy。
由图得 Vy = cosα * V0，gy = cosα * g，所以t = 2 * （cosα * V0）/ （cosα * g），约掉cosα得:
t = 2 * V0 / g，α由题中a，b决定。
由动能定理：mgh = 1/2 * m * V0^2 - 0，解得V0 = sqrt(2gh)。所以t = 2*sqrt(2gh)/g，h由题中给的x，y，a，b决定。
与此同时，在平行于斜面的方向上，小球受一个恒力，做匀加速直线运动。
所以综上，我们可以将每一个时间段t作为一次循环，去迭代小球的Vx和位移，直到位移大于落点到原点的距离。

题解代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <cmath>
#include <algorithm>
using namespace std;
typedef long long ll;
const int INF = 0x3f3f3f;
const double g = 9.8;

int main()
{
    int T;
    cin >> T;
    while(T--)
    {
        double a, b, x, y;
        scanf("%lf%lf%lf%lf", &a, &b, &x, &y);
        double tana = fabs(b) / fabs(a); //α的三个三角函数值
        double cosa = fabs(a) / sqrt(a*a+b*b);
        double sina = fabs(b) / sqrt(a*a+b*b);
        double h = fabs(x)*tana;
        double dis = sqrt(x*x + h*h); //落点到原点的距离
        double v0 = sqrt(2.0 * g * (y-h));
        double t = 2.0 * v0 / g; //每次小球从弹起到落下所花费的时间
        double vx = v0*sina;
        double gx = g*sina;
        int cnt = 0;//弹起的次数
        double s = 0; //走过的位移
        while(dis >= s)
        {
            s += (vx*t + 0.5*gx*t*t);
            vx += gx*t;
            cnt++;
        }
        printf("%d\n", cnt);
    }
    return 0;
}