一直想更博客了，一直没更，今天闲的没事，就把之前学习的树链剖分整理了一下。
预备知识：线段树，DFS序
DFS序
DFS序，字面意思，就是DFS到的顺序
我们只需要在搜到节点的时候记录一下就可以了
比如这样可能是一个树的DFS序
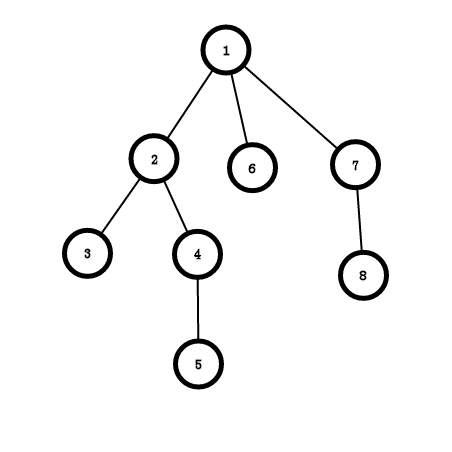
那知道了DFS序又有什么用呢
我们可以发现一颗子树在DFS序上是连续的一段
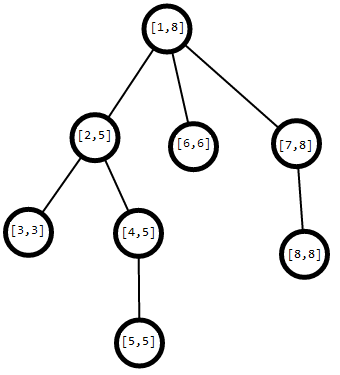
那么它就有了一个区间的性质，每个节点对应一段区间，那么我们在进行一些操作像什么：将以某节点为根的子树节点都加上x时，就可以转化为在线段树内的区间加了
树链剖分
首先我们要清楚一些概念：
重儿子（节点）：子树结点数目最多的结点
轻儿子（节点）：除了重儿子以外的结点
重边：父亲结点和重儿子连成的边
轻边：父亲节点和轻儿子连成的边
重链：由多条重边连接而成的路径
轻链：由多条轻边连接而成的路径
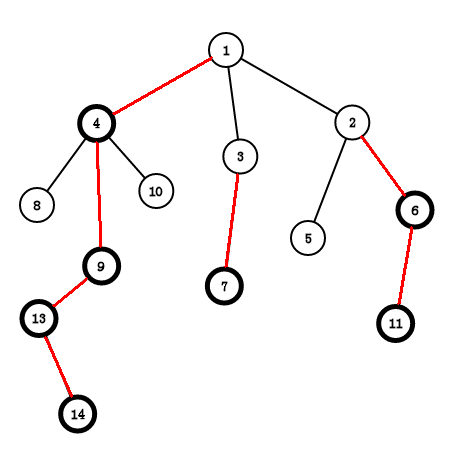
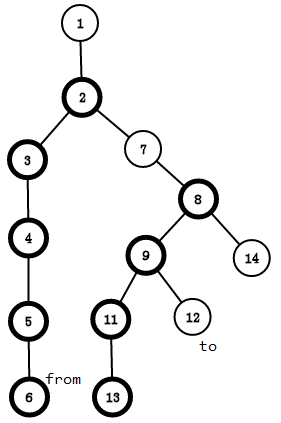
看图感受一下，
可以看到：对于1节点4的子树的节点比2,3的多，所以4是重儿子
对于4节点9的子树的节点比8,9的多，所以9是重儿子
以此类推
所以结果是：图中黑色的节点是重儿子，其余的节点是轻儿子
红边是重边，黑边是轻边
1 - 4 - 9 - 13 - 14；3 - 7；2 - 6 - 11是重链
我们发现：叶节点没有重儿子，非叶节点有且只有1个重儿子
并不是轻儿子之后全是轻儿子，比如3后面就有6和11两个重儿子
我们就可以这样理解：
当一个节点选了他的重儿子之后，我们并不能保证它的轻儿子就是叶节点，所以我们就以这个轻儿子为根，再去选这个轻儿子的轻重儿子
也就是一个DFS的过程，这样我们就会得到很多重链
有如下两个性质：
1.轻边(u,v)中, size(u)≤ size(u/2)
2.从根到某一点的路径上,不超过logn条轻链和不超过logn条重链。
那我们要怎么求出轻重儿子呢
这里我们定义几个数组：
son[u]：表示u的重儿子
size[u]：表示以u为根的树的节点个数，如上图的size[1] = 13
在这里，我们还可以顺带的求出
f[u]：节点的父节点
dep[u]：节点的深度
//u是当前节点
//fa是当前节点的父节点
void dfs1(int u, int fa) {
size[u] = 1;//表示刚搜到u的时候以u为根的子树里只有u一个节点
for (int i = head[u]; ~i; i = e[i].nx) { int v = e[i].v;//连向的节点 if (v != fa) {//因为连的是无相边，而且是树，不能往上搜，所以我们要判断u是不是从fa搜过来，也就是判断v是不是u的子节点，也可以写作!dep[v](没有被搜到过) dep[v] = dep[u] + 1;//v的深度是当前节点的深度+1 f[v] = u;//记录一下父亲 dfs1(v, u);//继续往下搜，一直搜到叶节点为止 size[u] += size[v];//往上回溯，更新以u为根的子树的size if (size[v] > size[son[u]]) son[u] = v;//重儿子是节点个数更多的子树，如果以u的子树中，以v为根的子树节点多，那就更新一下u的重儿子为v } } } 这样我们就求出了这棵树的所有重儿子，所有点的深度，和所有点的父亲。
既然我们已经求出来重儿子，轻儿子那么我们就要把他们连成链
因为我们要把轻重儿子连城链，所以我们就一定要让链上的点连续，方便我们的操作
那该怎么办呢，这就用到了我们之前提到的DFS序了
我们从根开始一遍DFS，如果有重儿子就先走重儿子（将一条重链放到一个区间内），搜到叶子节点后回溯回去再去搜轻儿子（轻链）
这一遍DFS里，我们又引入了几个数组：
top[u]：节点u所在链的顶端
id[u]：节点u的新编号（DFS序）
a[cnt]：在新编号（DFS序）下的当前点的点值
w[u]：题目中给出的节点u的点值
//u是当前节点
//t是所在链的顶端
void dfs2(int u, int t) {
id[u] = ++cnt;//给这个点一个新的编号
a[cnt] = w[u];//记录这个编号下点的值
top[u] = t;//记录u所在链的顶端为t
if (son[u]) dfs2(son[u], t);//u的重儿子和u在同一条链里
for (int i = head[u]; ~i; i = e[i].nx) { int v = e[i].v;//搜轻儿子 if (v != f[u] && v != son[u])//判断是否是轻儿子 dfs2(v, v);//以轻儿子为顶的链 } } 为什么是dfs2(v,v)呢，因为当v是重儿子的时候，它不可能为一条链的顶，因为根据重边的定义，一定有一条边连向重儿子，若重儿子为顶，还会有一条边连向它，所以重儿子不会为顶端。
树链剖分求LCA
为什么要先讲树剖求LCA呢
因为树剖的很多题是要求要在链上进行操作的，而链上操作其实就是LCA
树剖求LCA其实也是往上跳，但这里的往上跳不是倍增的往上跳
我们这里只要把两个点跳到同一条链里就好了
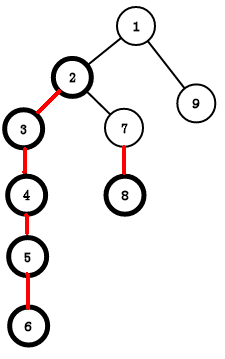
如图：我们要求LCA的话，有两种情况
1、在同一条链内，如3和5。这时直接输出深度较小的那个节点就好了
2、不再同一条链内，如6和8。因为他们不再一条链内，所以我们让其中一个点 x 直接跳到链的顶端也是没有问题的。这时我们就让那个深度深的 x 一直往上跳，这把 x 更新 x 的顶端的父亲节点，也就是到了另一条链上，记录一下它在这条新链上的顶端是谁，用来判断和另一个点 y 是否在同一条链内。当 x 跳到它所在的链的顶端时，深度可能就小于 y 的顶端了，也就是在另一条链的上面(这时 x 不会再往上跳，y 也不会再往上跳，但没有找到LCA)，这时我们就要交换他们（其实只是换了个名字，管原来的 y 叫 x ，管原来的 x 叫 y，原来的树并没有变，想了很久），保证 x , y 会更新到同一条链内
稍微模拟一下
如图：
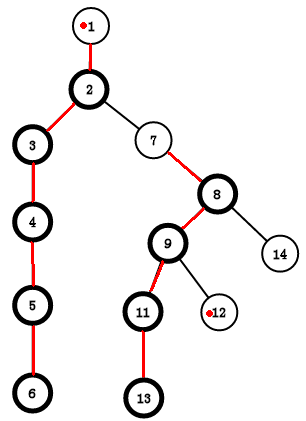
如果我们要求6和12的LCA
设x = 12,y = 1
这时我们先比较一下两者的top，fx = top[x] = 12，fy = top[y] = 1
发现他们的top不一样
那就往上跳呗，dep[fx] ＞ dep[fy]，所以 x = f[fx] = 9,fx = top[x] = 7
12往上跳跳到了9
变成了这样
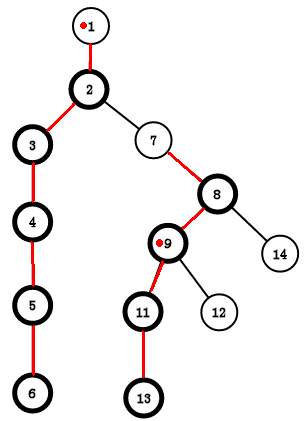
找到9所在链的顶为7
发现7 != 1说明9和1不再同一个链里
继续往上跳
x = top[fx] = 2，fx = top[2] = 1
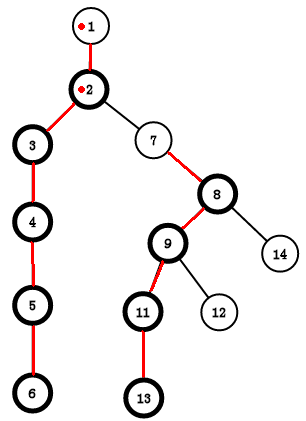
发现1 == 1
说明我们现在的 x 和 y 在同一条链里了
这时我们就返回深度小的那个就可以了
//fx表示x所在链的顶，fy表示y所在链的顶
int LCA(int x, int y) {
int fx = top[x], fy = top[y]; while (fx != fy) { if (dep[fx] < dep[fy]) swap(x, y), swap(fx, fy); x = f[fx], fx = top[x]; } return dep[x] < dep[y] ? x : y;//最后返回深度小的那个 } 如果还有边权的话，只要在dfs1里加1句话就可以了
void dfs1(int u, int fa) {
size[u] = 1; for (int i = head[u]; ~i; i = e[i].nx) { int v = e[i].v; if (v != fa) { dep[v] = dep[u] + 1; f[v] = u; dis[v] = dis[u] + e[i].w;//here dfs1(v, u); size[u] += size[v]; if (size[v] > size[son[u]]) son[u] = v; } } } dis[u]表示从根到u的距离，其实倍增，tarjan都是这么着
查询距离的时候还是
dis[x] + dis[y] - 2 * dis[LCA(x, y)]
路径上的修改/查询
讲完了LCA，剩下的路径上修改和查询就和LCA差不多了，只是加了几句话而已
这里要结合我们上面的DFS序和LCA
那对于路径上的操作，我们先想LCA，在求LCA的时候，我们每次都往上跳一条链，直到这两个点在一个路径上为止
就像我们刚开始的找6的top一样
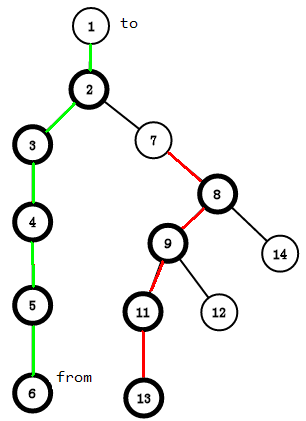
一次就经过了这么一条链（绿边）
我们再回想一下DFS序的性质，会得到在这一条链上，新的编号是连续的，我们要对这一条链进行修改和查询操作，这让我们想到了什么
线段树！！
线段树最支持的不就是区间修改和查询吗
那么我们就可以用线段树维护这一条路径了。
那如果我们要维护6到12这样一条路径呢？
还记得我们求LCA的时候是怎么往上跳的吗
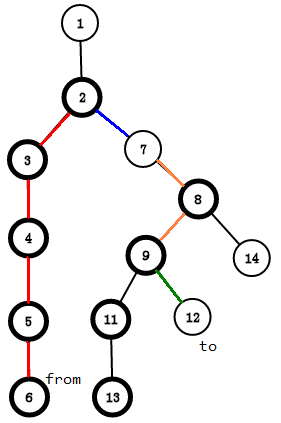
左半部分的12往上跳，每次都跳到所在链的顶端（只记录初末位置），我们可以得到12跳到的当前点 u 所处的链的顶的新编号（跳到9，顶为7），我们又知道当前点 u 的新编号，那我们就可以用线段树对从顶段到当前点 u 这条路径进行操作了，这样我们每次修改一条链（可能是一部分），就完成了路径的操作；
跳到2的时候，fx == fy，两点在同一条链内，x = 2，y = 6，然后我们操作 id[2] 到 id[6] ，这样我们就一条链一条链的完成了对这条路径的操作
全程我们操作的区间是[id[2],id[6]]，[id[7],id[9]]，[id[12],id[12]]
我们不对蓝边上的点和绿边上的点操作，因为他们不是重链，只是注明一下点经过的路径，若对它们操作的话会算重复
我刚写完这句话的时候想到了一个error
如果图长这样
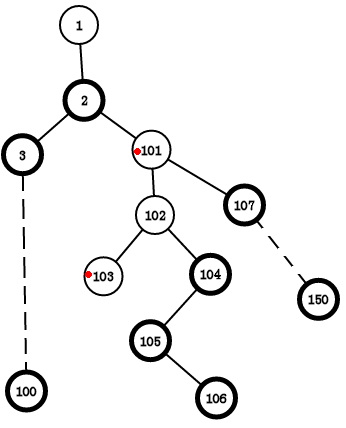（虚线是我省略了那一串的点）
如果我们要查询 103 到 101 呢，它们之间没有重链啊，那只好就一个一个的往上跳了，103->102->101.（退化成单点操作）
//修改
void update_chain(int x, int y, int z) {
int fx = top[x], fy = top[y]; while (fx != fy) { if (dep[fx] < dep[fy]) swap(x, y), swap(fx, fy); update(id[fx], id[x], z, 1, cnt, 1);//每往上跳一次，就修改以次经过路径上的值，因为DFS序中id[fx] < id[x]，所以是区间[id[fx],id[x]]; x = f[fx], fx = top[x]; } if (id[x] > id[y]) swap(x, y);//要保证区间是从小到大的 update(id[x], id[y], z, 1, cnt, 1); }
//查询
int query_chain(int x, int y) {
int ans = 0, fx = top[x], fy = top[y]; while (fx != fy) { if (dep[fx] < dep[fy]) swap(x, y), swap(fx, fy); ans += query(id[fx], id[x], 1, cnt, 1); x = f[fx], fx = top[x]; } if (id[x] > id[y]) swap(x, y); ans += query(id[x], id[y], 1, cnt, 1); return ans; } 到此为止，我们就完成了树链剖分的基本操作
若有什么错误或不足，还请不吝指出
求赞呐QAQ
京公网安备 11010502036488号