1. 最小二乘
Ax=b 经常会没有解,当方程个数大于未知数个数,也即 m>n 时,列空间并不是 Rm 空间的全部,因此 b 可能不在列空间中,这时候方程组就无解,但我们不应该就此而停止。
也就是误差 e=b−Ax 并不总是能得到 0,这时候,如果误差 e 的长度尽可能的小,那我们就得到了最小二乘解 x^。
当 Ax=b 无解的时候,我们乘以 AT 来求解 ATAx=ATb。
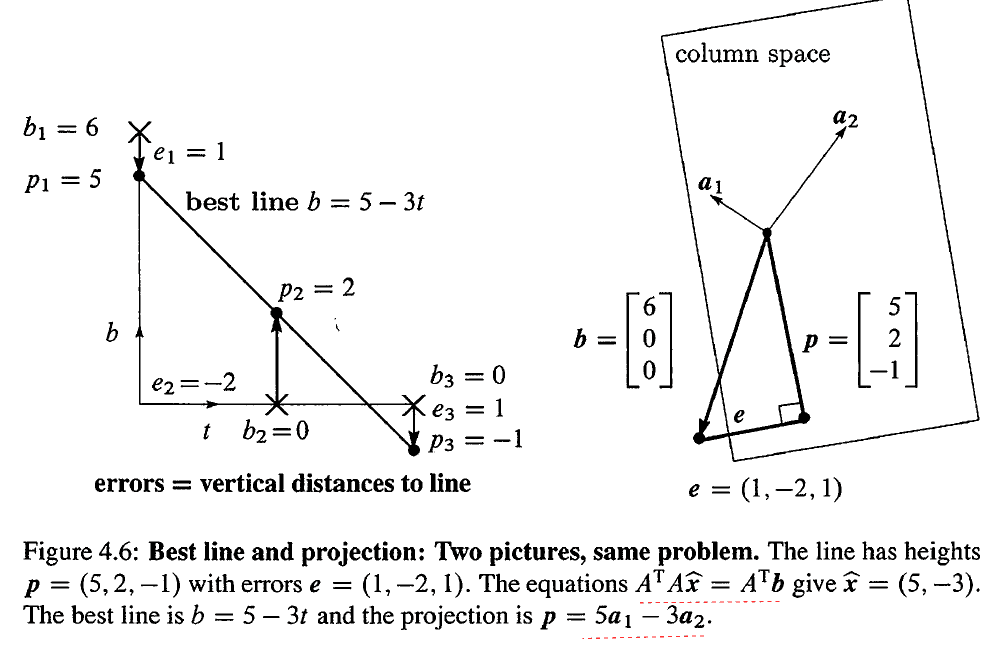
假如我们要找到一条直线,让它距离 (0, 6) ,(1, 0),(2, 0) 这三点最近。没有直线 b=C+Dt 同时穿过这三点,我们要找的两个常数 C 和 D。
C+C+C+DDD⋅0=6⋅1=0⋅2=0
A=⎣⎡111012⎦⎤x=[CD]b=⎣⎡600⎦⎤
由于 b=(6,0,0) 不是 A 的列的一个线性组合,因此方程组无解。
ATAx=ATb→[3335][CD][60]
C=5D=−3
因此,距离这三点最近的一条直线为 b=5−3t。
2. 最小化误差
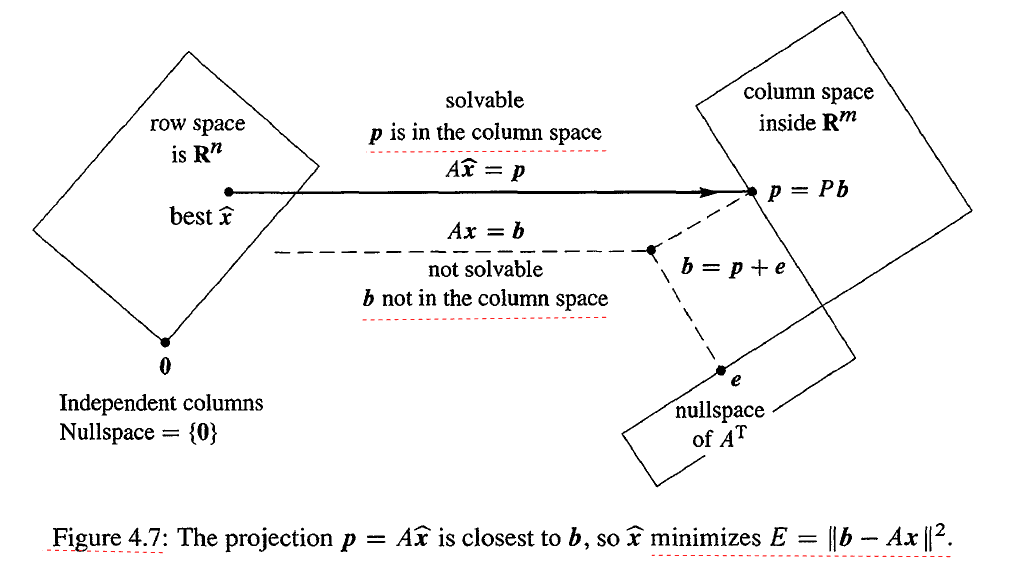
任何 Ax 都是 A 的列的一个线性组合,它们都位于以 A 的列为基的一个平面中。因此,我们要找的就是平面中的一个距离 b 最近的向量,而这个向量就是 b 在这个平面中的投影 p。
Ax=b=p+e 是不可解的,但 Ax^=p 是可解的。我们需要最小化下面这个误差
∣∣Ax−b∣∣2=∣∣Ax−p∣∣2+∣∣e∣∣2
当取 x=x^,$ ||Ax-p||^2 = 0$,因此最小误差为 ∣e∣∣2。
误差函数可以表示为
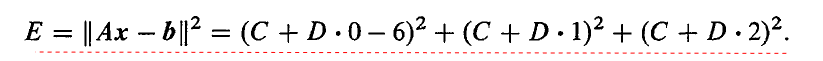
两个未知数有两个导数,当导数分别为零时,我们就得到了误差函数的最小值。
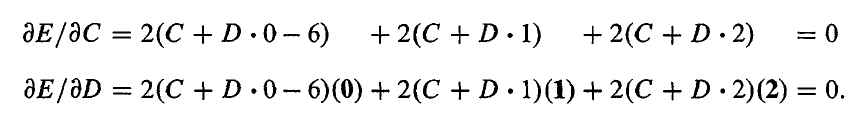
整理后我们得到
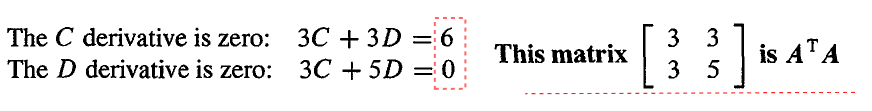
可以看到,这和 ATAx=ATb 得到的结果是一样的。也就是说当 ATAx=ATb 的时候 ∣∣Ax−b∣∣2 的偏导数为零。
在四个基本子空间中,这次我们将 b 分解为 b=p+e,这时候 ATAx=ATb 的零空间解只有零向量,因此最优解只有一个 Ax^=p。
获取更多精彩,请关注「seniusen」!





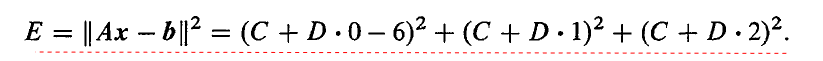
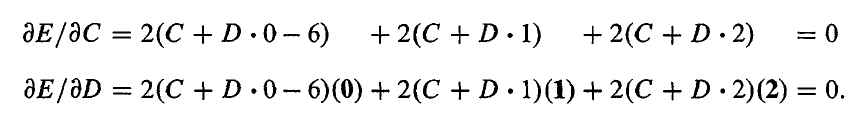
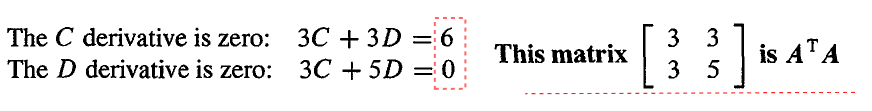



 京公网安备 11010502036488号
京公网安备 11010502036488号