【模板】二位前缀和

难度：3星

二维前缀和模板题。设 $sum[i][j]sum[i][j]$ 为左上角坐标为 $[0,0][0,0]$ ，右下角坐标为 $[i,j][i,j]$ 的子矩阵所有数之和。那么观察下图：

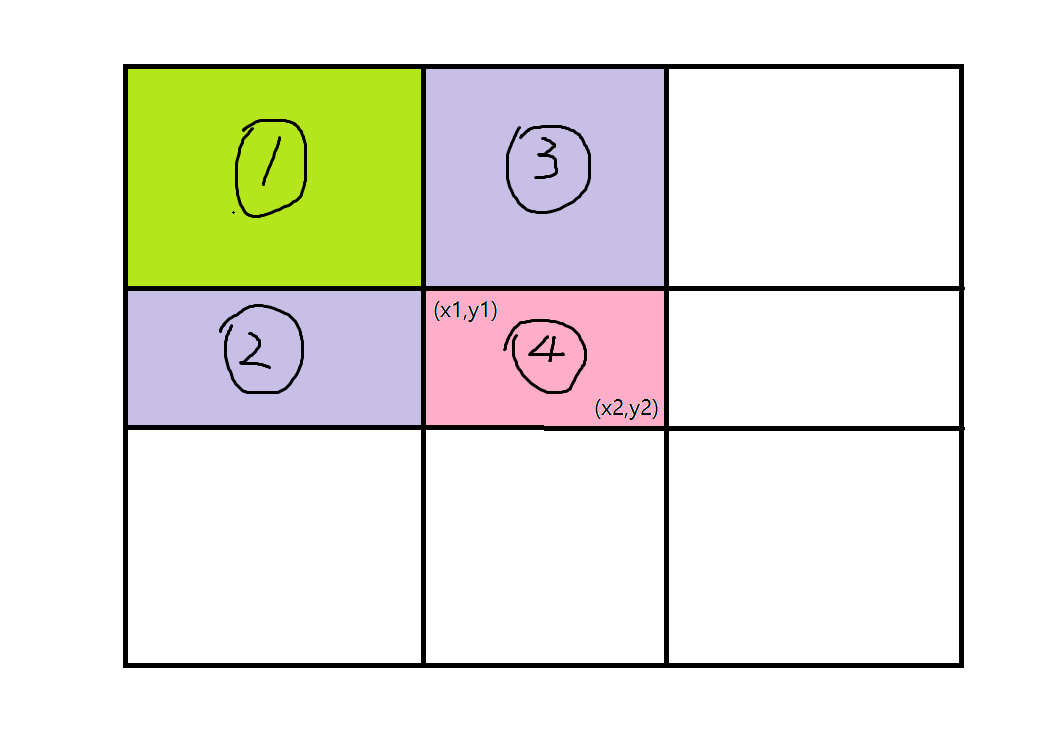
我们要求粉色部分的所有数之和（即④号），可以用下面的方式来求：

$sum[x_2][y_2]sum[x\_2][y\_2]$: ①+②+③+④

$sum[x_1-1][y_2]sum[x\_1-1][y\_2]$: ①+③

$sum[x_2][y_1-1]sum[x\_2][y\_1-1]$: ①+②

$sum[x_1-1][y_1-1]sum[x\_1-1][y\_1-1]$: ①

所以 $sum[x_2][y_2]-sum[x_1-1][y_2]-sum[x_2][y_1-1]+sum[x_1-1][y_1-1]sum[x\_2][y\_2]-sum[x\_1-1][y\_2]-sum[x\_2][y\_1-1]+sum[x\_1-1][y\_1-1]$ 即为我们所求的部分。

用更通俗的方式去理解，我们那大的子矩阵，减去左方和上面两个子矩阵之后，左上方的哪个绿的子矩阵被减了2次，所以要加回来。

#include<bits/stdc++.h>
using namespace std;
long long a[1010][1010];
int main(){
    int n,m,q;
    cin>>n>>m>>q;
    int i,j;
    for(i=1;i<=n;i++){
        for(j=1;j<=m;j++){
            cin>>a[i][j];
            a[i][j]+=a[i-1][j];
        }
    }
    for(j=1;j<=m;j++){
        for(i=1;i<=n;i++)a[i][j]+=a[i][j-1];
    }
    while(q--){
        int x_1,y_1,x_2,y_2;
        cin>>x_1>>y_1>>x_2>>y_2;
        cout<<a[x_2][y_2]-a[x_1-1][y_2]-a[x_2][y_1-1]+a[x_1-1][y_1-1]<<endl;
    }
}