计算机通过主元来计算行列式,但还有另外两种方法,一种是大公式,由 n! 项置换矩阵组成;另一种是代数余子式公式。
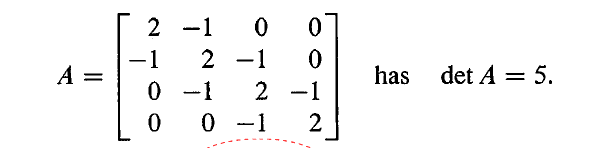
detA=16−4−4−4+1=5
16 来自于对角线上 4 个 2 的乘积,其余的通过公式我们也都可以找到。
- 代数余子式公式用第一行的数字 2,-1,0, 0分别乘以它们的代数余子式 4, 3, 2, 1,得到 8-3 = 5。
1. 主元公式
消元过程会让主元 d1,⋯,dn 最后出现在矩阵 U 的对角线上,如果没有行交换,那么有:
detA=(detL)(detU)=(1)(d1d2⋯dn)
如果有行交换,那么有 PA=LU 而且有 ∣P∣=±1,所以
detA=±(d1d2⋯dn)
如果主元的个数少于 n,那么 detA=0,矩阵是不可逆的。
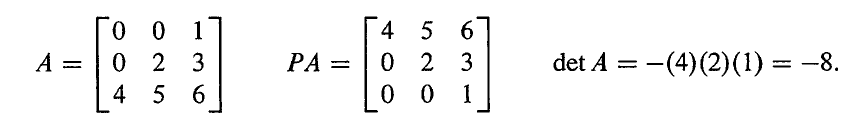
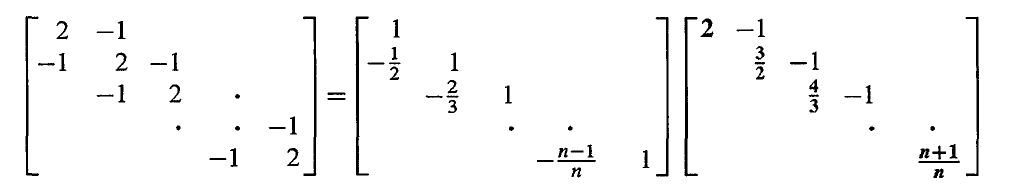
detA=2∗23∗34∗45⋯∗nn+1=n+1
而且,我们可以看到,前 k 个主元来自于矩阵 A 左上角大小为 k×k 的矩阵 Ak。
detAk=d1d2⋯dk
假设没有行交换,那在我们消元的过程中,有 Ak=LkUk,因此
det Ak−1det Ak=det Uk−1det Uk→dk=d1d2⋯dk−1d1d2⋯dk−1dk
2. 大公式
大公式直接利用矩阵中的每一个元素来计算行列式,一个 3×3 矩阵的计算公式如下所示。
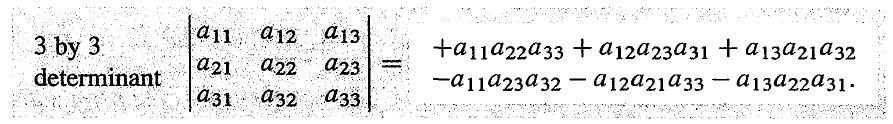
注意到,每一项乘积的三个元素都分别来自于矩阵中的三行和三列,而其前面的符号其实是由置换矩阵来决定的。
由行列式的线性性质我们可以将一个 2×2 矩阵的行列式分成四项:
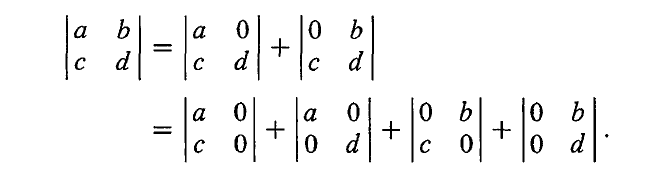
其中,第一个和第四个行列式为 0,因为它们有全零列。因此,只余下 2!=2 项需要计算。

对于一个 3×3 的矩阵,其行列式可以分成 27 项,但只有 6 个非零项。

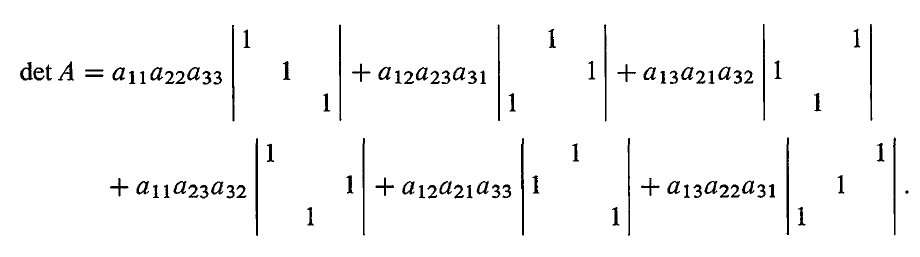
前面三个置换矩阵有偶数次行交换,因此其行列式为 1;而后面三个置换矩阵有奇数次行交换,因此其行列式为 -1。
因此,矩阵 A 的行列式是 n! 项简单行列式的和,每一项的系数是 1 或者 -1,其中简单的行列式是从每一行每一列中选取一个元素组成。

3. 代数余子式公式
利用行列式的线性性质,我们将第一行的三个元素分别提取出来,可以得到。

其中,括号里面的项称为代数余子式(cofactor),它们是 2×2 矩阵的行列式。第一行贡献出因子 a11,a12,a13,余下的行贡献出代数余子式 C11,C12,C13,然后行列式的值就是 a11C11+a12C12+a13C13。

接下来,我们需要注意符号。要计算 C1j,我们划掉第 1 行第 j 列来产生一个大小为 n−1 的子矩阵 M1j,然后
C1j=(−1)1+jdet M1j
det A=a11C11+a12C12+⋯+a1nC1n
注意,对其它行来说,也有同样的情况。对 Cij 来说,我们划掉第 i 行第 j 列来产生一个大小为 n−1 的子矩阵 Mij。

Cij=(−1)i+jdet Mij
det A=ai1Ci1+ai2Ci2+⋯+ainCin
同时,行列式也可以沿着某一列进行计算。
det A=a1jC1j+a2jC2j+⋯+anjCnj
代数余子式公式在矩阵中有许多零时是非常有用的。

获取更多精彩,请关注「seniusen」!




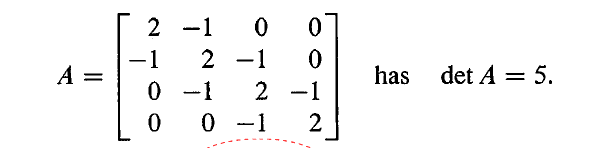
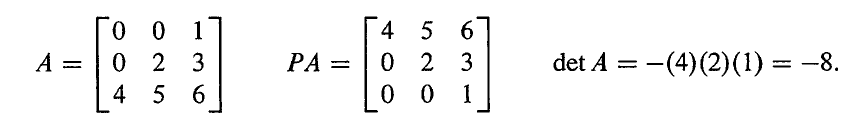
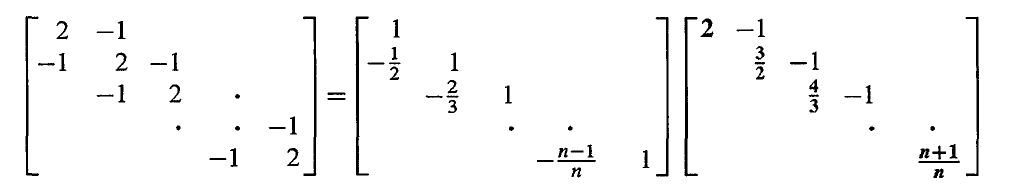
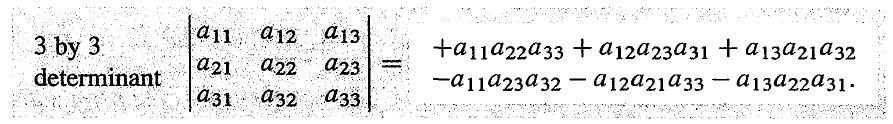
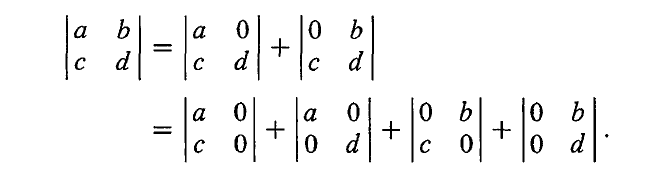


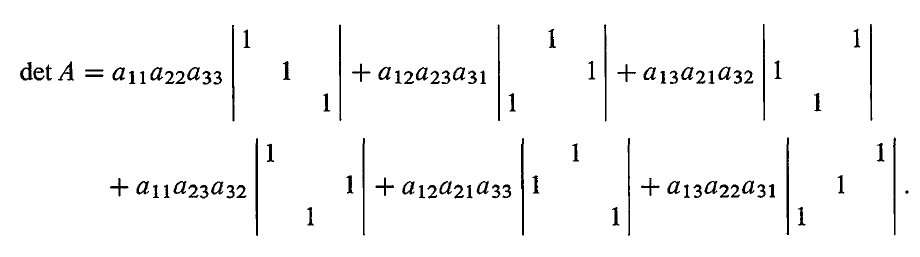







 京公网安备 11010502036488号
京公网安备 11010502036488号