分配问题——线性规划模型

题目简述

$nn$ 个人分配给 $mm$ 个工作岗位 $(n⩾m)(n\; \backslash geqslant\; m)$，每个岗位 $11$ 个人。已知第每个人在每个岗位上的效率，求最佳分配方案使得所有人的效率总和最大。

设立变量

设立变量 $x_{i,j}x\_\{i,j\}$，$1⩽i⩽n1\backslash leqslant\; i\; \backslash leqslant\; n$，$1⩽j⩽m1\backslash leqslant\; j\; \backslash leqslant\; m$，$x_{i,j}=0x\_\{i,j\}=0$或$11$。 $x_{i,j}=1x\_\{i,j\}=1$ 表示第 $ii$ 个人做第 $jj$ 个工作，$x_{i,j}=0x\_\{i,j\}=0$ 则表示第 $ii$ 个人不做第 $jj$ 个工作。

设立变量 $c_{i,j}c\_\{i,j\}$，$1⩽i⩽n1\backslash leqslant\; i\; \backslash leqslant\; n$，$1⩽j⩽m1\backslash leqslant\; j\; \backslash leqslant\; m$。$c_{i,j}c\_\{i,j\}$ 表示第 $ii$ 个人在第 $jj$ 个上的效率。

目标函数

$z_{max}(x_{i,j})={\sum }_{i=1}^n{\sum }_{j=1}^m{c}_{i,j}\times x_{i,j}z\_\{max\}(x\_\{i,j\})=\backslash sum\_\{i=1\}^\{n\}\backslash sum\_\{j=1\}^\{m\}c\_\{i,j\}\; \backslash times\; x\_\{i,j\}$

一个人的岗位选择中为 $11$ 的那个是他选择的岗位，将总和加上他在这个岗位工作的效率。如果是 $00$ 就不加了。目标函数就是求 $z(x_{i,j})z(x\_\{i,j\})$ 的最大值。

限制条件

• $x_{i,j}=0x\_\{i,j\}=0$或$11$（取值范围）

• ${\sum }_{i=1}^n{x}_{i,j}=1,1⩽j⩽m\backslash sum\_\{i=1\}^\{n\}x\_\{i,j\}=1,1\backslash leqslant\; j\; \backslash leqslant\; m$（每个岗位有且仅有一个人）

• ${\sum }_{j=1}^m{x}_{i,j}⩽1,1⩽i⩽n\backslash sum\_\{j=1\}^\{m\}x\_\{i,j\}\backslash leqslant\; 1,1\backslash leqslant\; i\; \backslash leqslant\; n$（每个人最多参与一个岗位）

模型求解

1. 生成数据

先假设 $n=8n=8$，$m=6m=6$，然后使用 Excel 随机生成 $c_{i,j}c\_\{i,j\}$ 的值，数据范围为 $[0,10)[0,10)$。 $x_{i,j}x\_\{i,j\}$ 也是一张 $n\times mn\; \backslash times\; m$ 的表格。

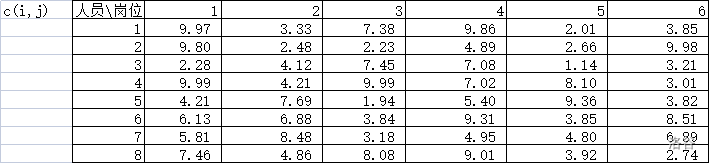
2. 目标函数

随意带入 $x_{i,j}x\_\{i,j\}$ 的值，将 $z(x_{i,j})z(x\_\{i,j\})$ 的值用公式算出。

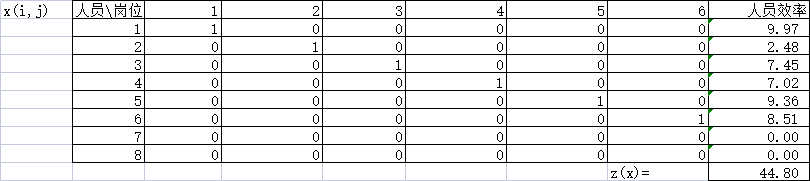
2. 限制条件

将限制条件相关的值用公式算出，并且加入 $x_{i,j}x\_\{i,j\}$ 为二进制的约束。

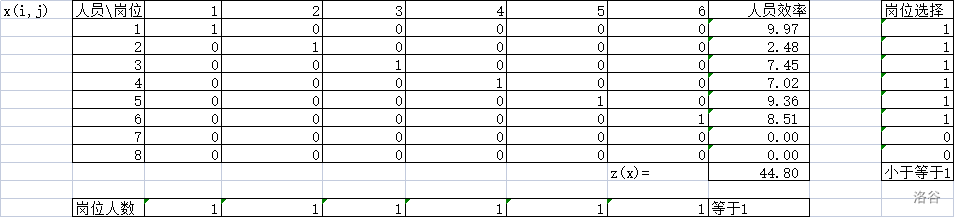
3. 模型求解

将所有变量和限制条件加入，使用 Excel 求出最优 $x_{i,j}x\_\{i,j\}$ 和对应的 $z_{max}(x_{i,j})z\_\{max\}(x\_\{i,j\})$。

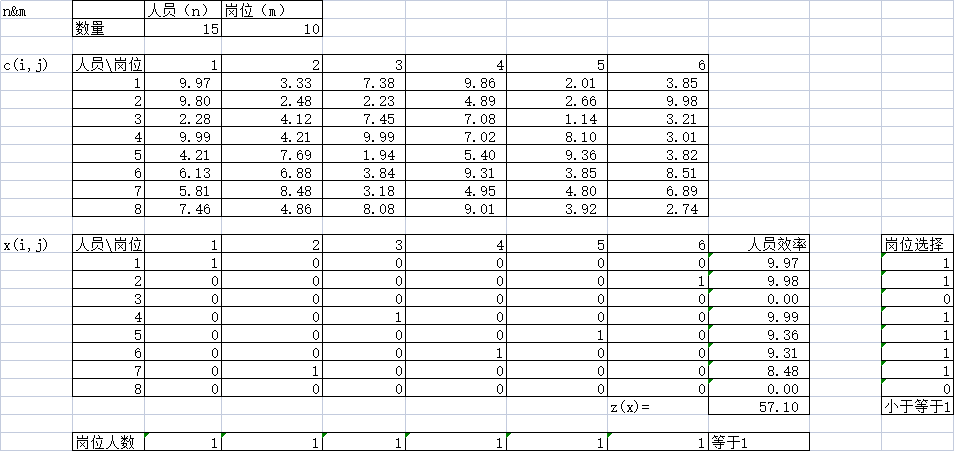
最终求得 $z_{max}(x_{i,j})=57.1z\_\{max\}(x\_\{i,j\})=57.1$，$x_{i,j}x\_\{i,j\}$ 如上图所示。