本算法建议谨慎使用，否则一不小心就会变成模拟退役
爬山算法
爬山算法是一种贪心搜索，每次从当前状态的所有后继状态中选择一个最优解继续搜索，直到达到一个局部最优解后不再搜索。
优点：好写
缺点：容易陷入局部最优解出不来
就像下图一样
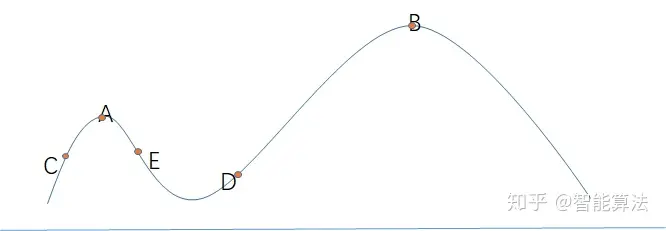
多随机几个初始状态就能减小(不能消除)缺点
模拟退火
模拟退火来源于金属的冷却过程
先看看金属冷却：
温度高时，金属内能较大，原子活动范围大。
温度低时，金属内能较小，原子活动范围小。
我们搜索的时候也类似，设一个变量T，可以理解为金属冷却过程中的温度
T(温度)初始值很大，但是搜索过程中每走一步就乘上一个小于1的常数。
搜索过程中从当前状态随机搜索（这个随机的范围也和T有关）就能找到下一步可以走的一个状态，那走不走呢？这里给出一个策略：下一步可以走的一个状态如果比当前好就直接走，否则，T越大，选择走的概率越大。
要注意，上一句话中下一步可以走的一个状态可能会比当前状态好，也可能差。
通俗一点来说的话：
T比较大的时候，即使下一个状态会变坏，也会大概率转移
T比较小的时候，下一个状态会变坏的时候只会小概率转移，类似爬山算法
可以看最下面那个视频理解
为了保证正确性，可以多做几轮。
或者可以用上ctime，控制程序运行时间,卡题目时限，在规定时间多运行几次
就像下面这样
while(clock()<Time){}
注意不同的系统返回的时间的单位可能不同!
所以可以写成这样
while((DB)clock()/CLOCKS_PER_SEC<=多少秒){}
其中(DB)clock()/CLOCKS_PER_SEC是程序运行的时间，单位是秒
P1337 [JSOI2004]平衡点 / 吊打XXX 题解
在各种题目中都能用到，正确性不能保证，很少用作正解，但好的时候能媲美标算。
还有在各种提交答案题中都能用到
附：模拟退火可视化视频
京公网安备 11010502036488号