二分图:
二分图又称作二部图,是图论中的一种特殊模型。 设G=(V,E)是一个无向图,如果顶点V可分割为两个互不相交的子集(A,B),并且图中的每条边(i,j)所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B),则称图G为一个二分图。——摘自百度百科
二分图匹配:
给定一个二分图G,在G的一个子图M中,M的边集中的任意两条边都不依附于同一个顶点,则称M是一个匹配.
 -_-||暂时不考虑特殊的性取向),如果一对男女互有好感,那么你就可以把这一对撮合在一起,现在让我们无视掉所有的单相思(好忧伤的感觉
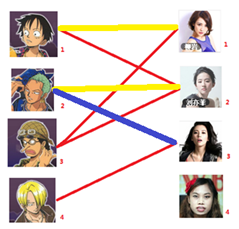
-_-||暂时不考虑特殊的性取向),如果一对男女互有好感,那么你就可以把这一对撮合在一起,现在让我们无视掉所有的单相思(好忧伤的感觉 ),你拥有的大概就是下面这样一张关系图,每一条连线都表示互有好感。
),你拥有的大概就是下面这样一张关系图,每一条连线都表示互有好感。 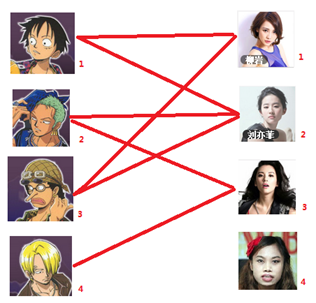
本着救人一命,胜造七级浮屠的原则,你想要尽可能地撮合更多的情侣,匈牙利算法的工作模式会教你这样做:
一: 先试着给1号男生找妹子,发现第一个和他相连的1号女生还名花无主,got it,连上一条蓝线
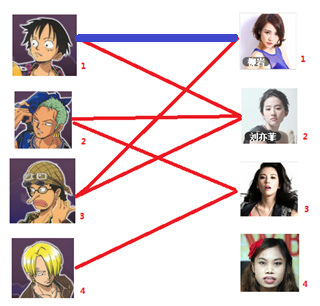
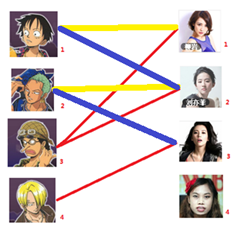
二:接着给2号男生找妹子,发现第一个和他相连的2号女生名花无主,got it
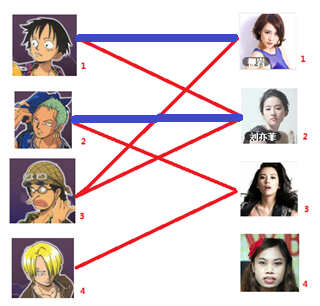
三:接下来是3号男生,很遗憾1号女生已经有主了,怎么办呢?
我们试着给之前1号女生匹配的男生(也就是1号男生)另外分配一个妹子。
(黄色表示这条边被临时拆掉)
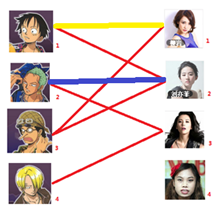
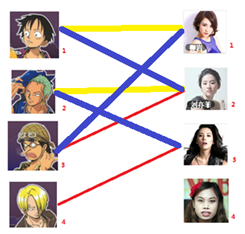
与1号男生相连的第二个女生是2号女生,但是2号女生也有主了,怎么办呢?我们再试着给2号女生的原配(
 )重新找个妹子(注意这个步骤和上面是一样的,这是一个递归的过程)
)重新找个妹子(注意这个步骤和上面是一样的,这是一个递归的过程)

此时发现2号男生还能找到3号女生,那么之前的问题迎刃而解了,回溯回去
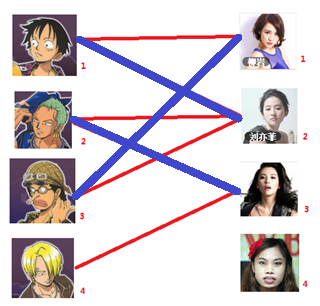
四: 接下来是4号男生,很遗憾,按照第三步的节奏我们没法给4号男生腾出来一个妹子,我们实在是无能为力了……香吉士同学走好。
PS:以上内容均借(fu)鉴(zhi)于一位大佬的博客
然后就完成了二分图匹配。
一道例题:luogu2756
代码:


1 #include<cstdio> 2 #include<iostream> 3 #include<cstring> 4 using namespace std; 5 const int N=110*2; 6 int n,m,girl[N],used[N],edg[N][N],boy[N]; 7 bool found(int x) 8 { 9 for(int i=m+1;i<=n;++i) 10 { 11 if(!used[i]&&edg[x][i]) 12 { 13 used[i]=1; 14 if(!girl[i]||found(girl[i])) 15 { 16 girl[i]=x; 17 boy[x]=i; 18 return 1; 19 } 20 } 21 } 22 return 0; 23 } 24 int main() 25 { 26 scanf("%d%d",&m,&n); 27 int x,y; 28 do 29 { 30 scanf("%d%d",&x,&y); 31 edg[x][y]=1; 32 }while(x!=-1||y!=-1); 33 int ans=0; 34 for(int i=1;i<=m;++i) 35 { 36 memset(used,0,sizeof(used)); 37 if(found(i)) ans++; 38 } 39 if(ans==0) 40 { 41 printf("No Solution!"); 42 return 0; 43 } 44 printf("%d\n",ans); 45 for(int i=1;i<=m;++i) 46 { 47 if(boy[i]) 48 printf("%d %d\n",i,boy[i]); 49 } 50 return 0; 51 }
网络流做法
建立超级源点S和超级汇点T,然后将S与每个”男生“连一条容量为1的边,从每个“女生”向T连一条容量为1的边,然后跑最大流即可。在dfs的过程中记录下每个“男生”的妹子
上面那道题的网络流代码:


1 #include<queue> 2 #include<cstdio> 3 #include<cstring> 4 #include<iostream> 5 using namespace std; 6 const int N=110; 7 const int INF=0x7fffffff; 8 queue<int>q; 9 struct node 10 { 11 int v,nxt,w; 12 }e[N*N]; 13 int head[N*N],ejs=0,S,T; 14 void add(int u,int v,int w) 15 { 16 e[++ejs].v=v;e[ejs].w=w;e[ejs].nxt=head[u];head[u]=ejs; 17 e[++ejs].v=u;e[ejs].w=0;e[ejs].nxt=head[v];head[v]=ejs; 18 } 19 int n,m,dep[N*N]; 20 bool bfs() 21 { 22 memset(dep,0,sizeof(dep)); 23 while(!q.empty()) q.pop(); 24 q.push(S); 25 dep[S]=1; 26 while(!q.empty()) 27 { 28 int u=q.front(); 29 q.pop(); 30 for(int i=head[u];i;i=e[i].nxt) 31 { 32 int v=e[i].v; 33 if(!dep[v]&&e[i].w) 34 { 35 dep[v]=dep[u]+1; 36 if(v==T) 37 return 1; 38 q.push(v); 39 } 40 } 41 } 42 return 0; 43 } 44 inline int change(int x) 45 { 46 return x%2?x+1:x-1; 47 } 48 int son[N*3]; 49 int dfs(int u,int dist) 50 { 51 if(u==T) 52 return dist; 53 for(int i=head[u];i;i=e[i].nxt) 54 { 55 int v=e[i].v; 56 if(dep[v]==dep[u]+1&&e[i].w) 57 { 58 int k=dfs(v,min(dist,e[i].w)); 59 if(k) 60 { 61 62 son[u]=v; 63 e[i].w-=k; 64 e[change(i)].w+=k; 65 return k; 66 } 67 } 68 } 69 return 0; 70 } 71 int dinic() 72 { 73 int ans=0; 74 while(bfs()) 75 { 76 77 int k=dfs(S,INF); 78 while(k) 79 { 80 ans+=k; 81 k=dfs(S,INF); 82 } 83 } 84 return ans; 85 } 86 int main() 87 { 88 scanf("%d%d",&m,&n); 89 int x=0,y=0; 90 T=m+n+1,S=0; 91 for(int i=1;i<=m;++i) 92 add(S,i,1); 93 for(int i=m+1;i<=n+m;++i) 94 add(i,T,1); 95 scanf("%d%d",&x,&y); 96 while(x!=-1||y!=-1) 97 { 98 add(x,y,1); 99 scanf("%d%d",&x,&y); 100 } 101 int k=dinic(); 102 if(!k) 103 { 104 printf("No solution!"); 105 return 0; 106 } 107 printf("%d\n",k); 108 for(int i=1;i<=m;++i) 109 { 110 if(son[i]) 111 printf("%d %d\n",i,son[i]); 112 } 113 return 0; 114 }




 京公网安备 11010502036488号
京公网安备 11010502036488号