Description

骰子大家一定都玩过。
一个骰子有六个面，每个面都有一个数字。对于骰子的每一个面，你都可以通过朝一个方向翻转90度来获得另一个面。




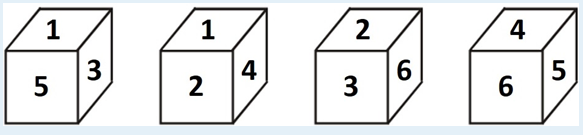
现在你有一个骰子，一开始朝上的一面点数为1（如图上的第一个骰子所示）。
你每次都可以将它朝一个方向翻转90度，并获得相当于翻转之后的骰子朝上一面的点数的分数。比如，现在骰子朝上的一面点数为1，你可以通过翻转使它朝上的一面变成3，并获得3分。

现在给出一个目标分数s，请问你至少需要翻转几次，使得你的分数刚好等于目标分数。

Input

题目包含多组测试数据。
第一行是一个整数T，表示有T组测试数据。
对于每组测试数据，只有一个正整数s,表示你需要达到的目标分数。(1 <= s <= 10000)

Output

对于每组测试数据，输出达到目标分数至少需要翻转几次,如果无解请输出-1。

Sample Input

2 5 10

Sample Output

1 2

Hint

对于第二组样例: 你可以先翻转90度，使得骰子朝上的一面变为4，并获得4分。 之后你可以再翻转90度，使得骰子朝上的一面变为6，并获得6分。 所以你至少需要2步来达到目标分数。

题解：

BFD了解一下

C++版本一

还没上传过emmm大概这个思路

#include <iostream>
#include<stdio.h>
#include<string.h>
#include<math.h>
#include<algorithm>
#include<queue>
using namespace std;
int ta,n,m;
int vis[100000];
struct node{
 int u;
 int a;
 int c;
}s,t,f;
queue<node>q;
int bfs(){
    while(!q.empty())
        q.pop();
    s.u=1;
    s.a=1;
    s.c=0;
    q.push(s);
    vis[1]=1;
    while(!q.empty()){
        f=q.front();
        q.pop();
        if(f.a==n)
            return f.c;
        if(f.a>n)
            continue;
        for(int i=1;i<=6;i++ ){
            if(i==t.u||i==7-t.u)
                continue;
            t=f;
            t.a+=i;
            if(!vis[t.a]){
                t.u=i;
                t.c++;
                vis[t.a]=1;
                q.push(t);
            }
        }
    }
    return -1;
}
int main()
{
    scanf("%d",&ta);
    while(ta--){
        scanf("%d",&n);
        memset(vis,0,sizeof(vis));
        printf("%d\n",bfs());
    }
    return 0;
}

C++版本二

某位大佬AC的代码

#include<stdio.h>
#include<string.h>
#include<algorithm>
#include<queue>
using namespace std;
const int maxn=10000;
const int INF=0x3f3f3f3f;
int vis[maxn+3];
int fq[maxn+3];
struct Node
{
    int ns;
    int score;
}hgf,dzb;
queue<Node>q;
int bfs()
{
    while (!q.empty())
    {
        dzb=q.front();
        q.pop();
        if (vis[dzb.score]) continue;
        if (dzb.score>maxn) continue;
        vis[dzb.score]=1;
        for (int i=1;i<=6;i++)
        {
            if (dzb.ns!=i&&dzb.ns!=(7-i))
            {
                hgf.ns=i;
                hgf.score=dzb.score+i;
                q.push(hgf);
                fq[hgf.score]=min(fq[hgf.score],fq[dzb.score]+1);
            }
        }
    }
    return 0;
}
int main()
{
    memset(vis,0,sizeof(vis));
    memset(fq,INF,sizeof(fq));
    fq[0]=0;
    int t,s;
    hgf.ns=1;
    hgf.score=0;
    q.push(hgf);
    bfs();
    scanf("%d",&t);
    while (t--)
    {
        scanf("%d",&s);
        if (fq[s]==INF) printf("-1\n");
        else printf("%d\n",fq[s]);
    }
    return 0;
}