GAMES101 现代计算机图形学入门（三）（四）

第三节课

本节主要讲了图形学的基本知识

Scale缩放

Reflection Matrix反射

Shear Matrix切边

Rotate旋转

Affine Transformations

Affine map = linear map + translation

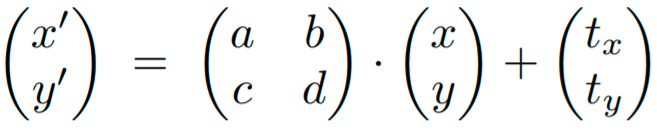
image-20210408170113892

Using homogenous coordinates:

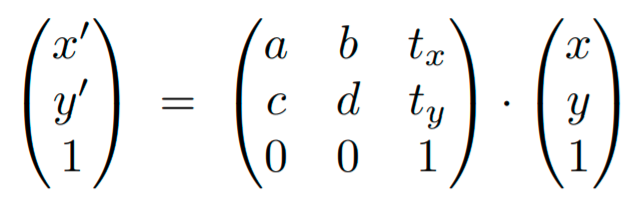
image-20210408170137607

Scale

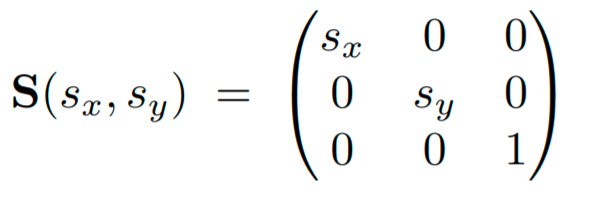
image-20210408200803251

Rotation

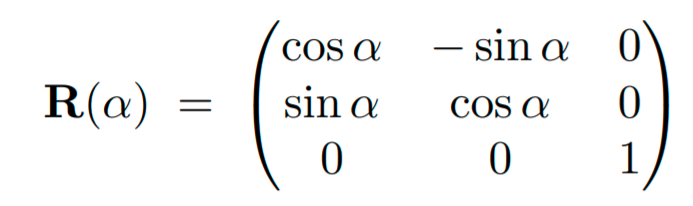
image-20210408200817674

Translation

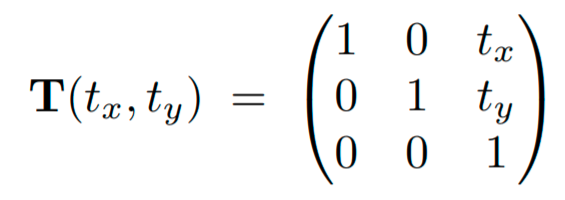
image-20210408200833920

Composing Transforms

Sequence of affine transforms

  • Compose by matrix multiplication
    • Very important for performance!
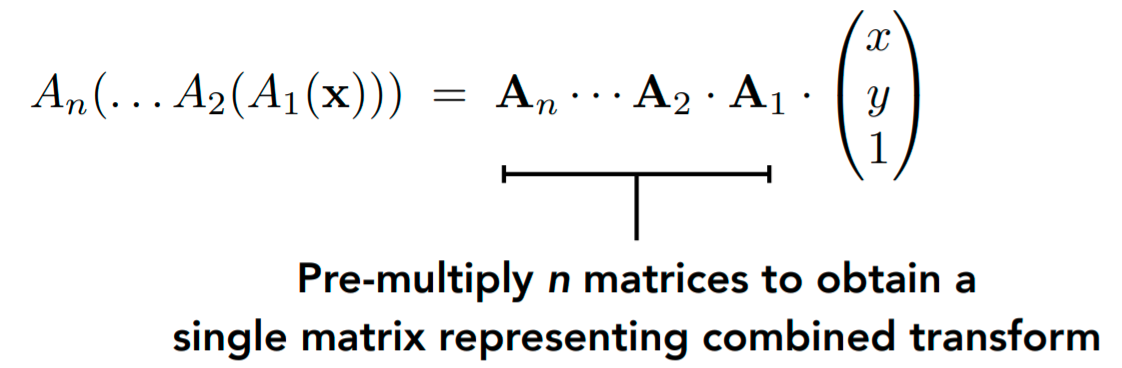
image-20210408205610558

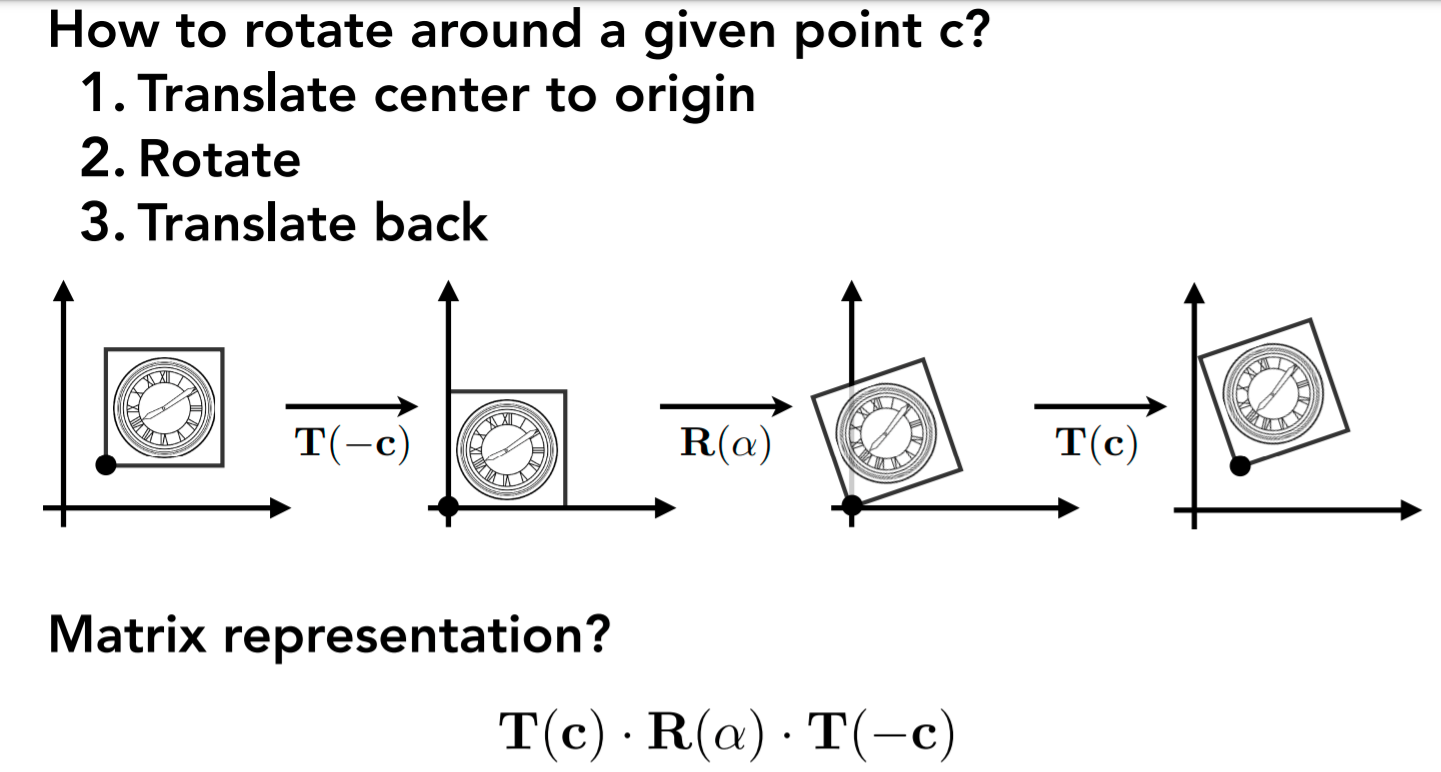
我觉得这节课最精髓的地方就是对于变换组合的处理，比如，你可能已经想到，这里面提到的旋转都是绕原点进行的，那么怎么绕平面上非原点的一点c进行旋转，该怎么操作呢？

答案是：将图形移到原点进行操作后，再移回来

image-20210408210646052

最后简单介绍了一下三维空间中的变换。

第四节课

因为第三节和第四节课的内容关联很大，所以笔记没有将两部分分割，

三维空间中的仿射变换，就是平移变换和线性变换与二维空间中的变换没有什么区别，十分相似。

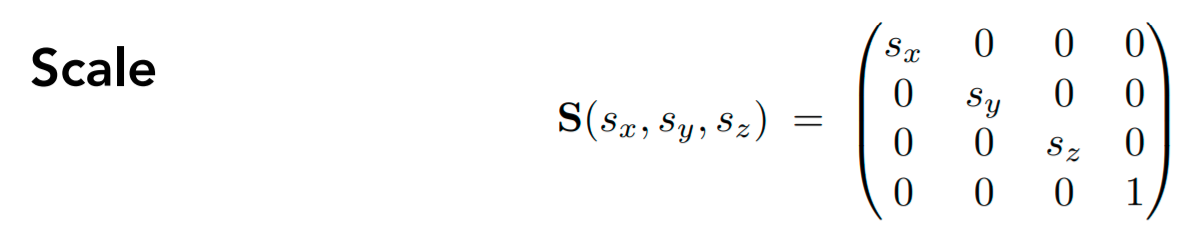
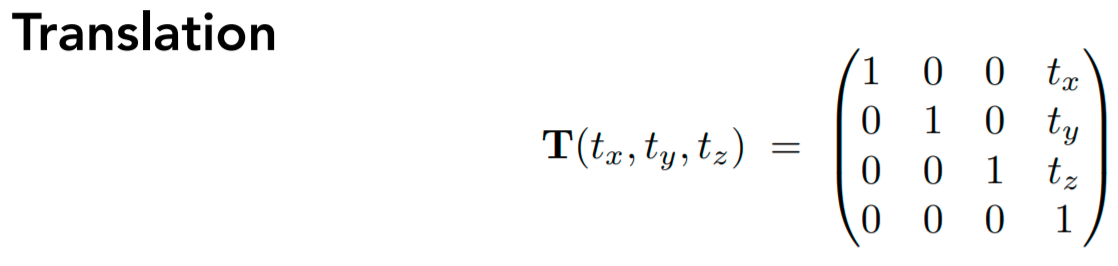
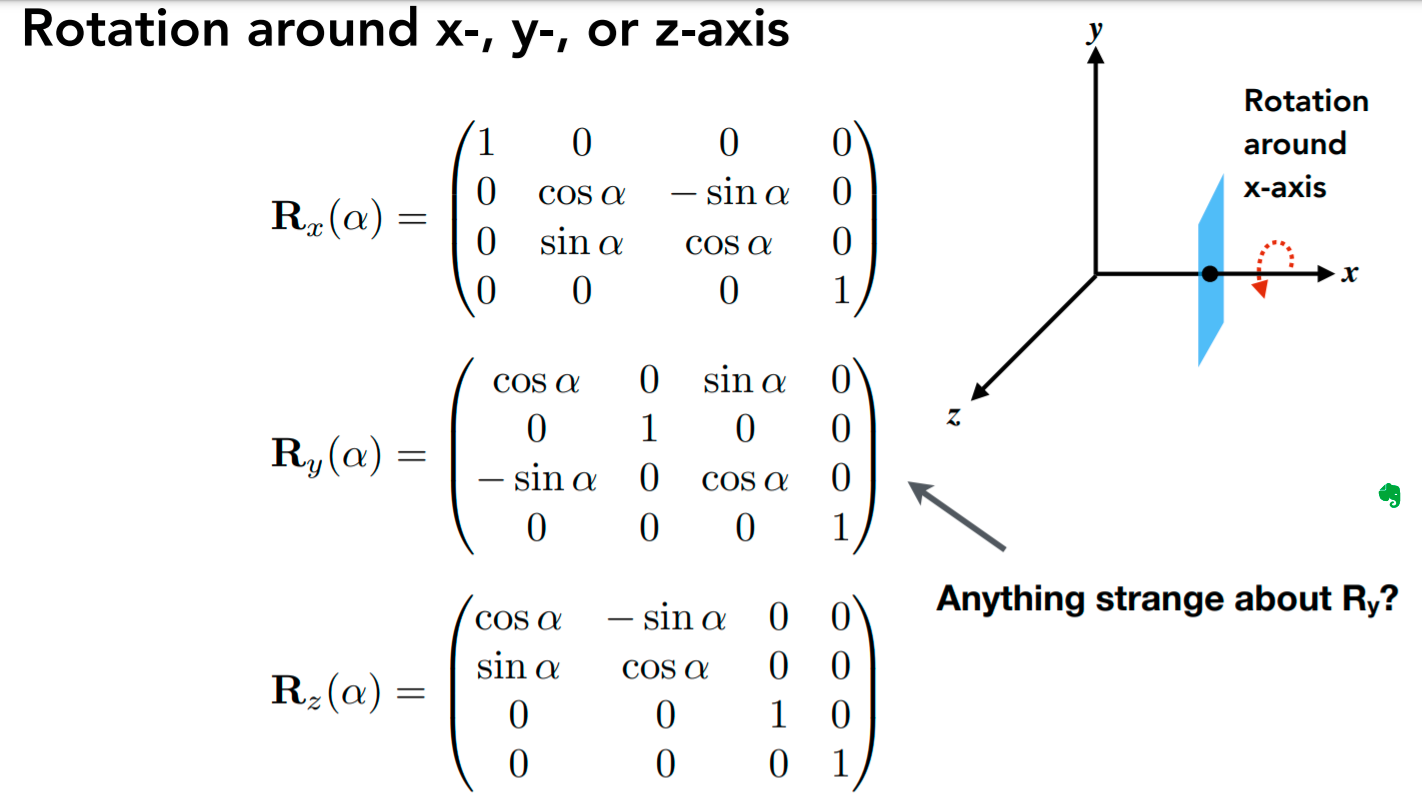
image-20210409112004233 image-20210409112017339 image-20210409112131805

绕y轴旋转和xz很不一样，闫老师解释的很清楚，xyzxyzxyz有循环对称的性质，在右手系的前提下，绕y轴旋转对于xz的坐标来说，逆时针是反向旋转角度，所以代入也应该代入的是负数。

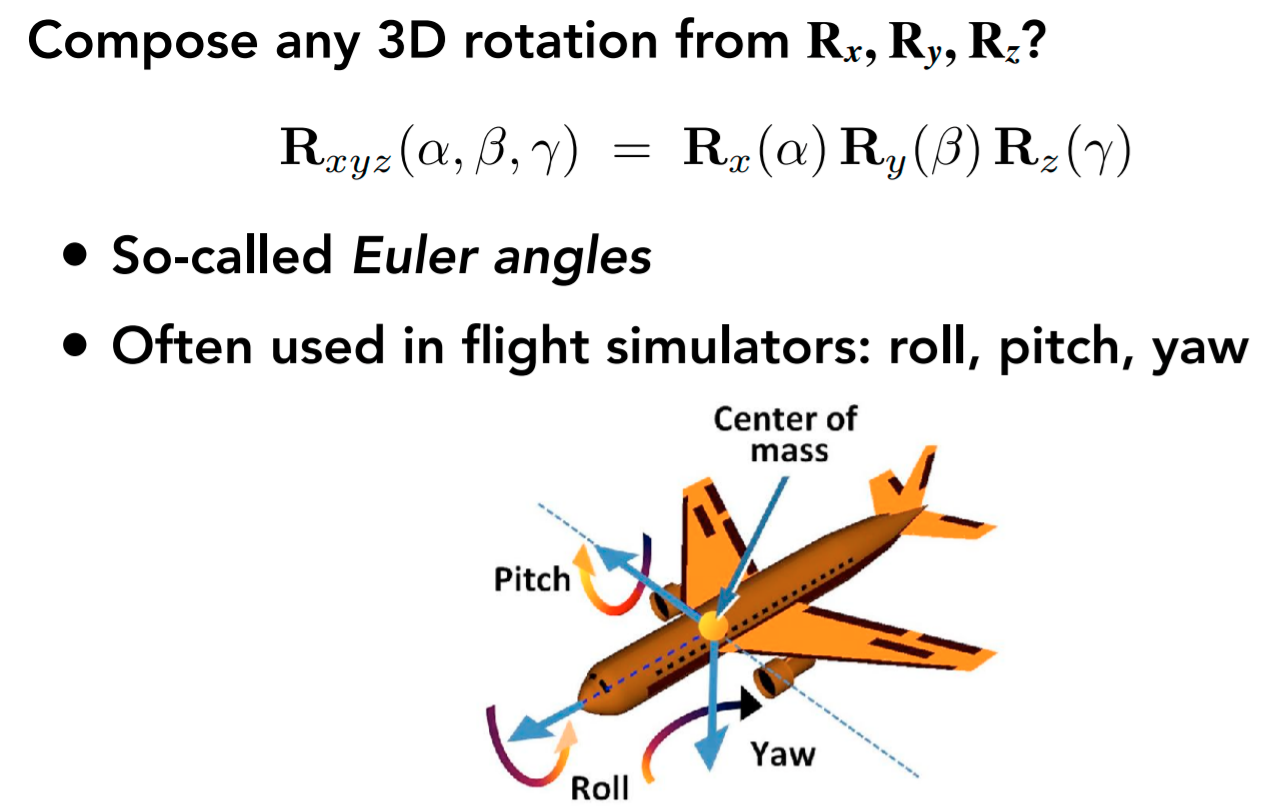
image-20210409113134879

roll：侧身

yaw：水平转圈

pitch：上下抬头

可以想象的是游戏里开飞机

image-20210409113940477

罗德里格斯旋转公式

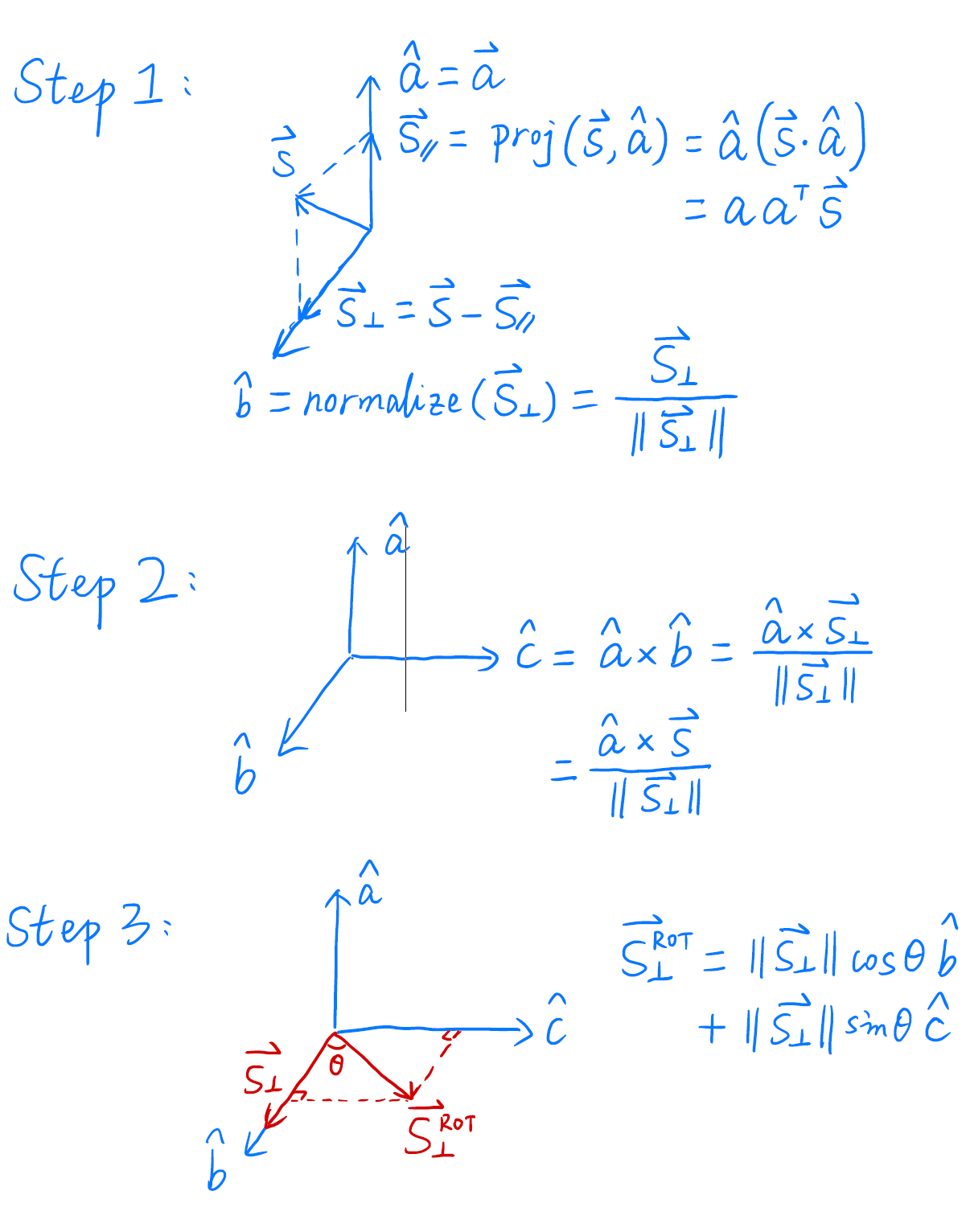
image-20210409142803934

三维空间绕任意轴旋转矩阵的推导：说实话，我没有太看懂闫老师的推导过程，但是知乎上有一篇三维空间绕任意轴旋转矩阵的推导很不错。

https://zhuanlan.zhihu.com/p/56587491

接下来主要讲

  • ==Viewing== transformation
    • View / Camera transformation
    • Projection transformation
      • Orthographic projection
      • Perspective projection

学了这么多东西，主要的目的是学会将三维空间中的东西变成二维，怎样呈现在显示器上

MVP变换：就是model，view，projection模型视图投影变换

闫老师举了一个非常好的例子，把MVP变换举例成如何去拍照片的过程

今天主要提到的就是视图变换VIEW

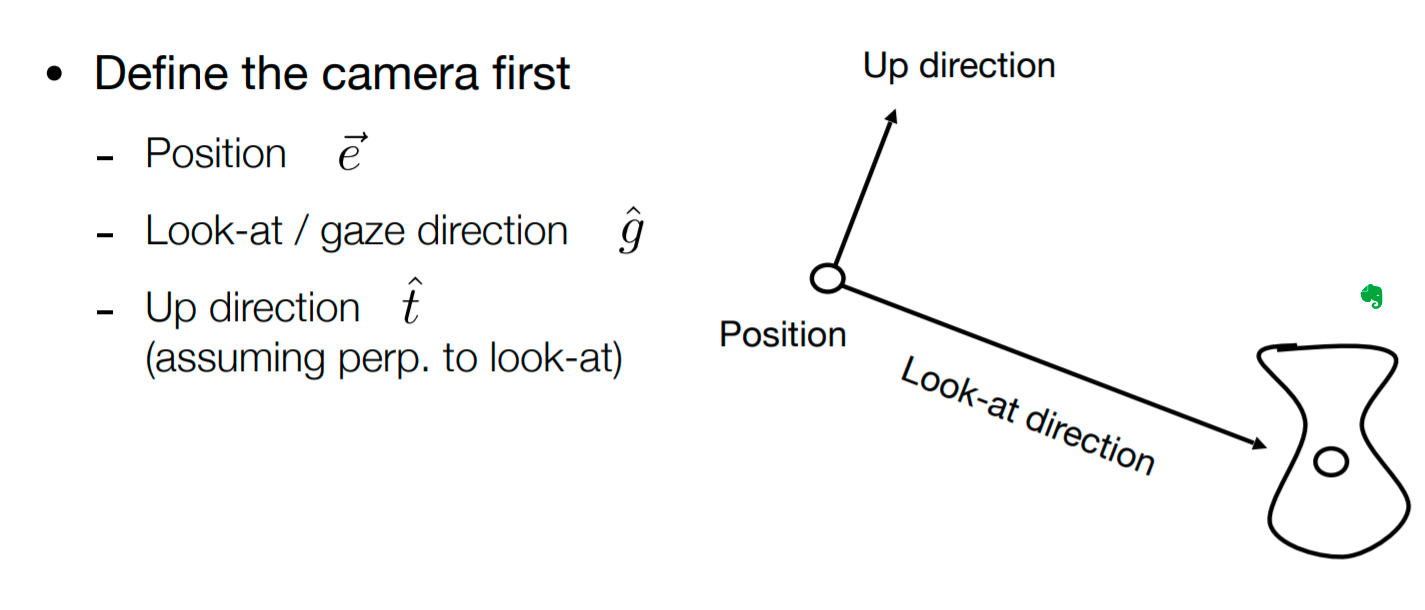
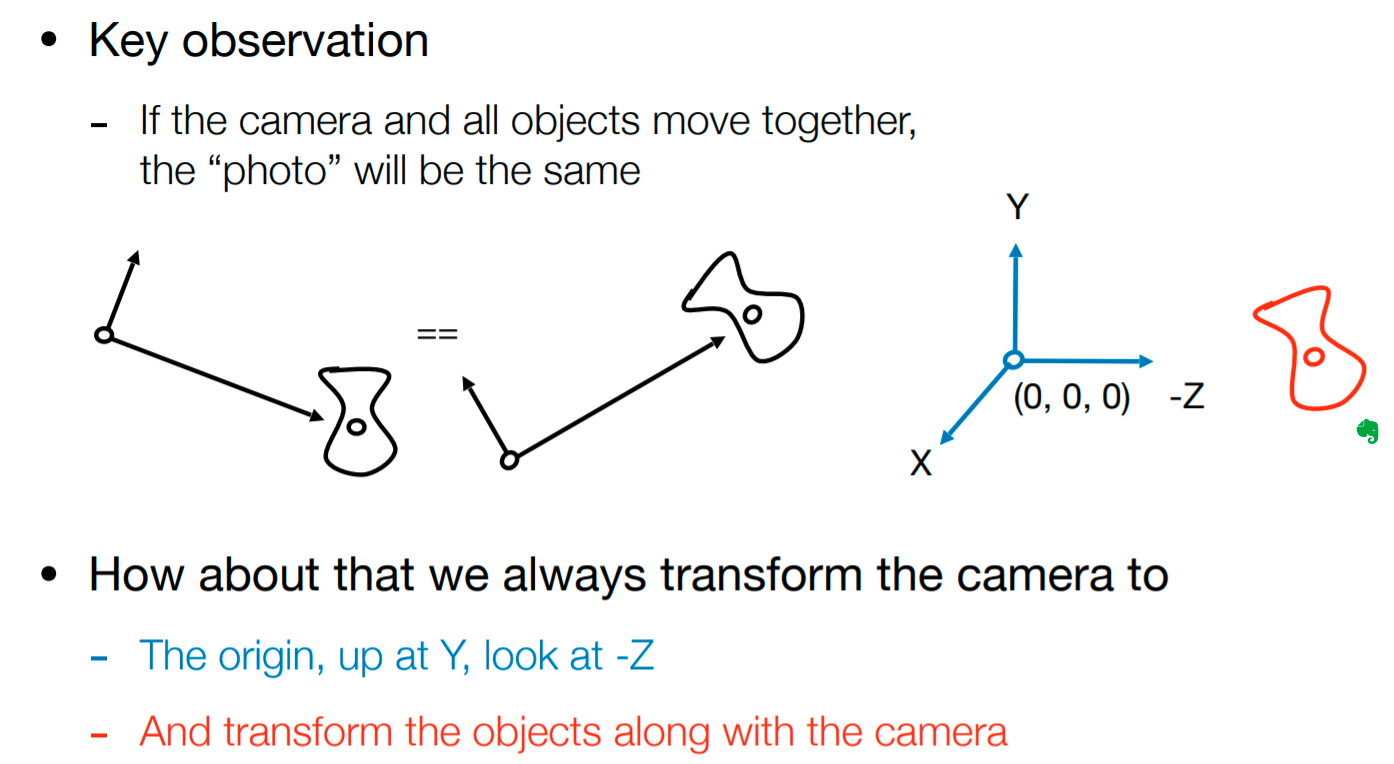
image-20210409162230412 image-20210409163257031

如何将相机从原有的摆放位置固定到想要的位置呢，首先将相机的位置移到原点，然后让原有的看的方向移到-z方向，注意这里是-z，然后将向上的方向移动到y的方向，最后x的方向肯定也重合了

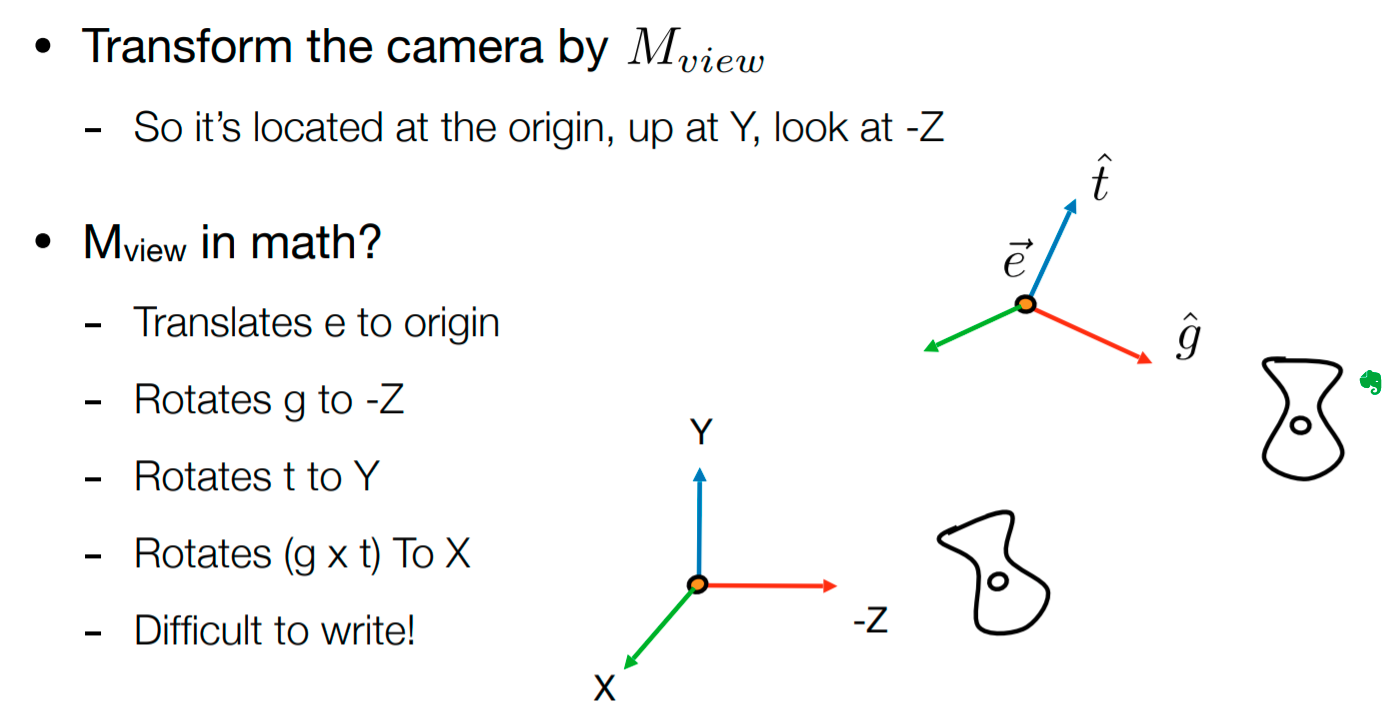
image-20210409164045037 image-20210409164512929

为什么要先求逆变换呢，是因为原始的变换不好求，从数学上讲，好求的是求逆变换，再求逆变换的逆，这就很好理解了。

旋转矩阵是正交矩阵

image-20210409181841289

RUA！一切为了投影变换！！！

首先来看正交投影

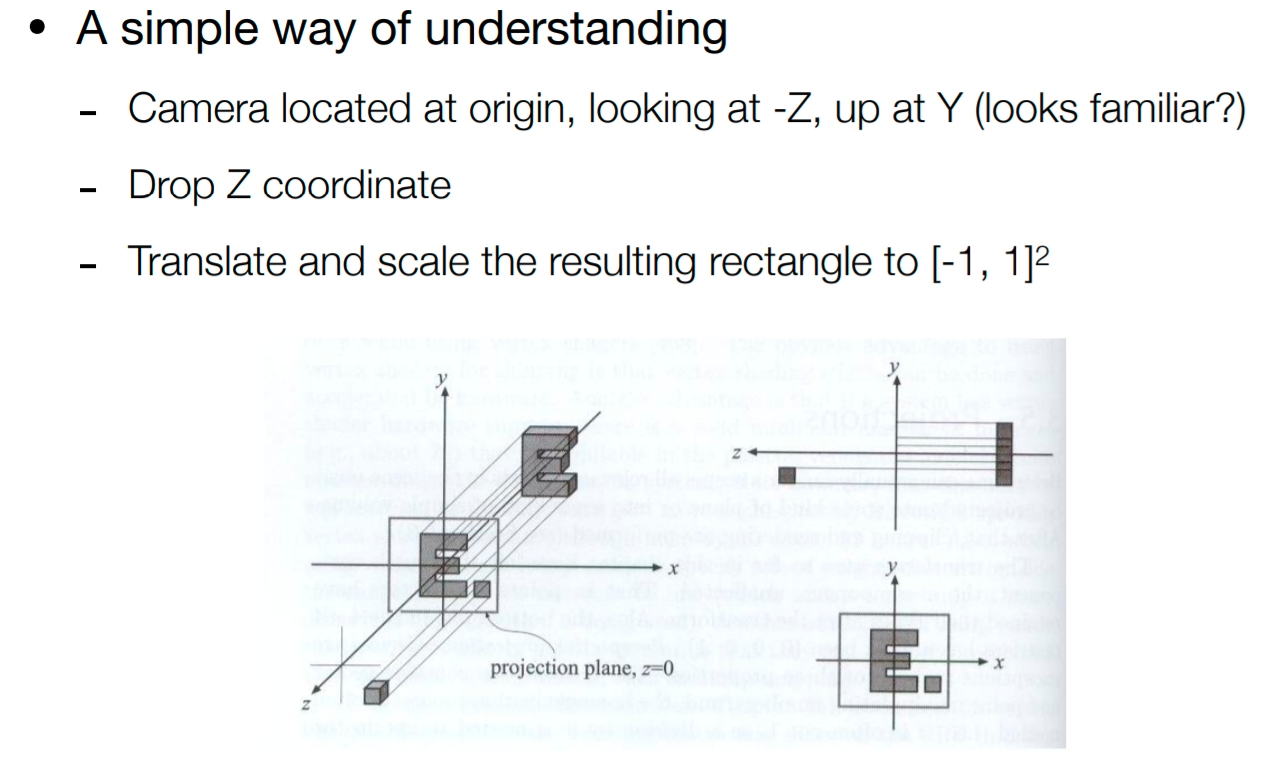
image-20210409185212245

但这种操作不是一般的做法，一般的做法是要canonical（正则）化

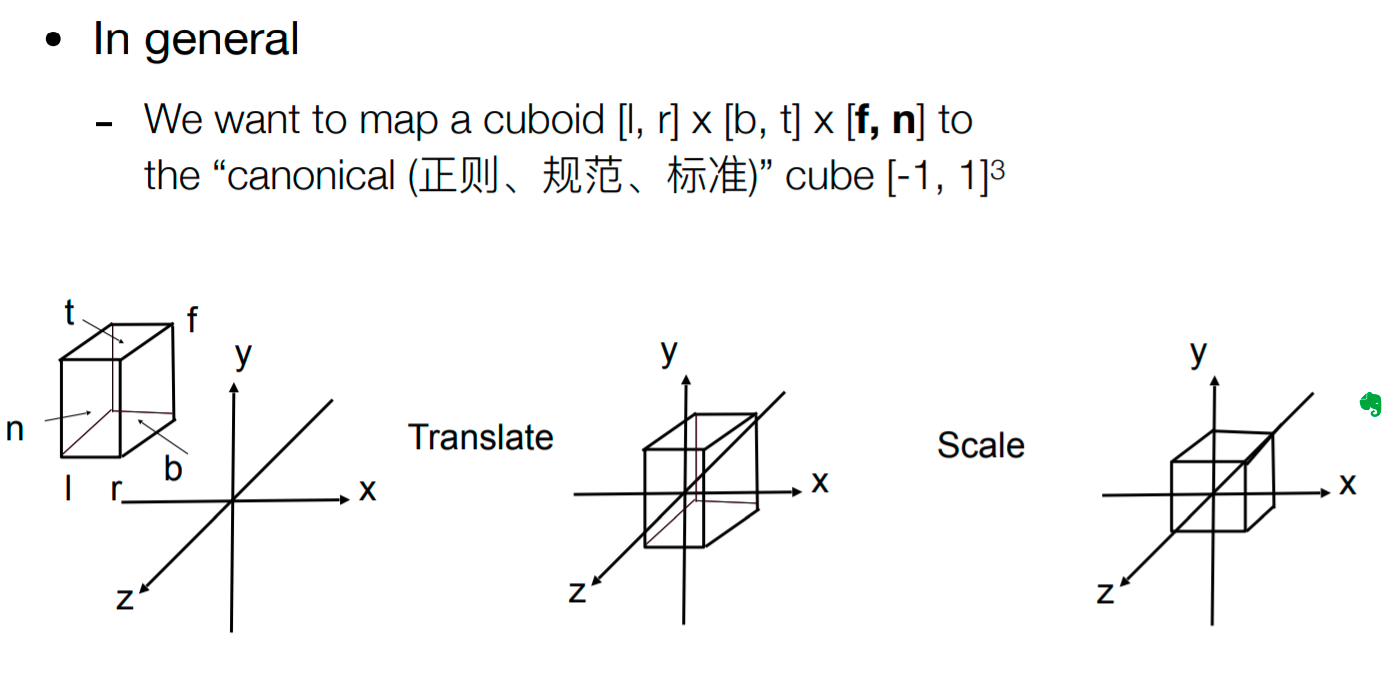
image-20210409185506380

空间中无论是啥长方体，统统映射到标准立方体上

image-20210409190233549

为什么OpenGL里面会使用左手系是因为，在判断远近的时候，右手系中越远的点，z轴上的数越小，这一点与常识违背。

image-20210409195145855

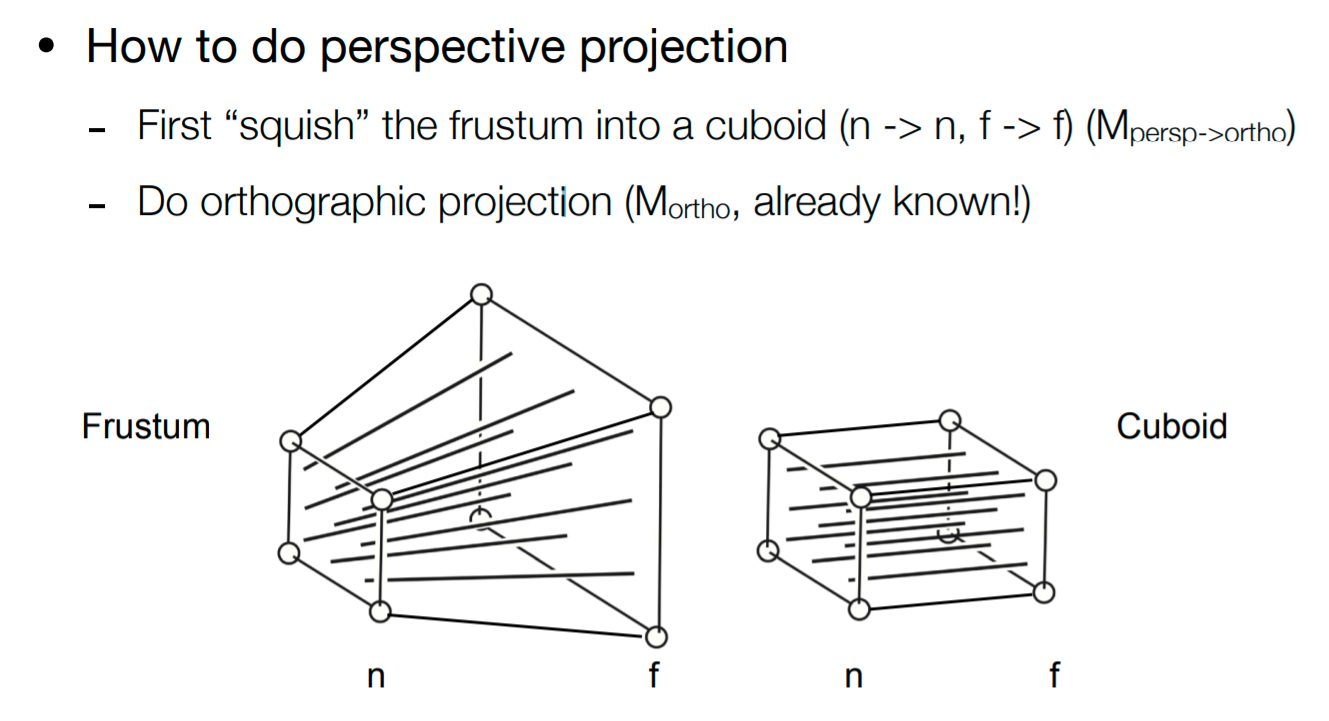
下面的部分就是透视投影

image-20210409200133112

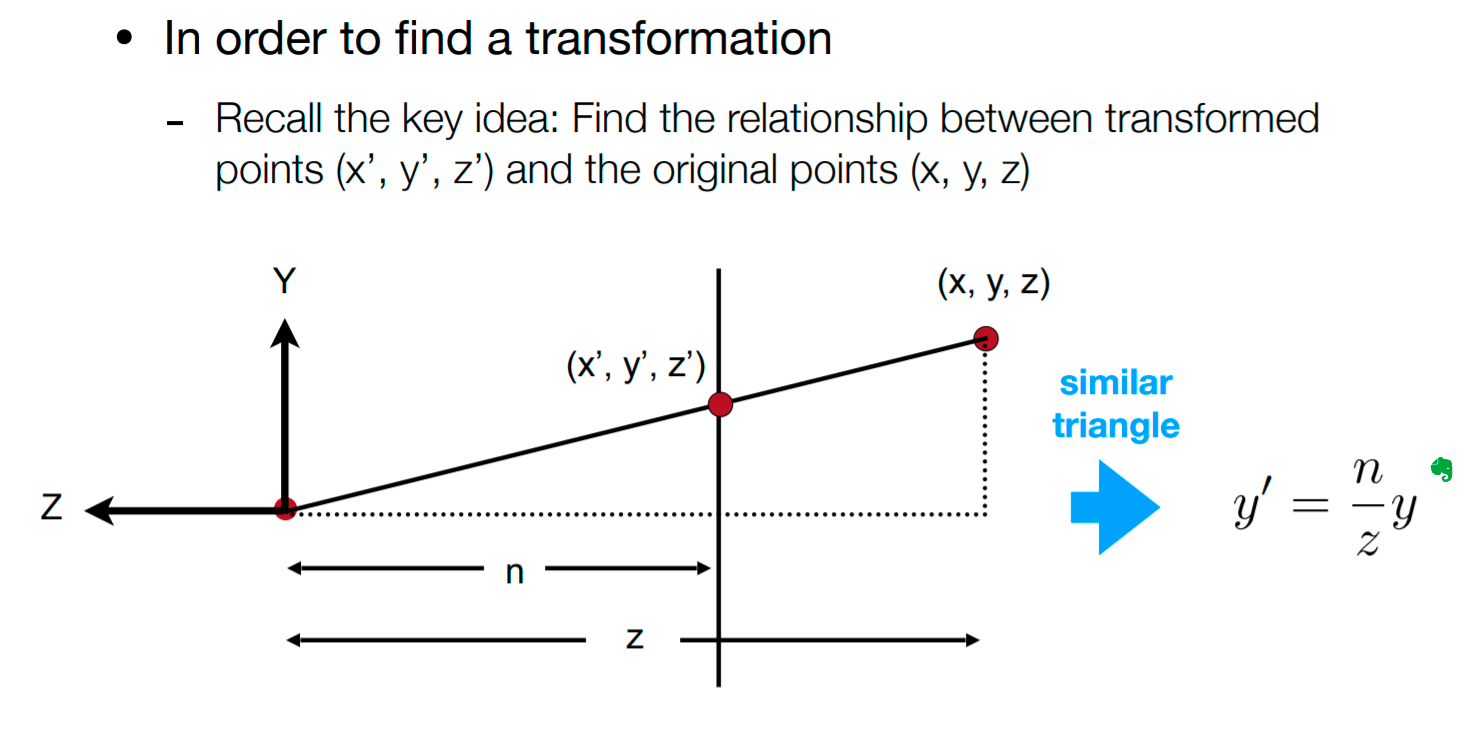
利用相似三角形的关系

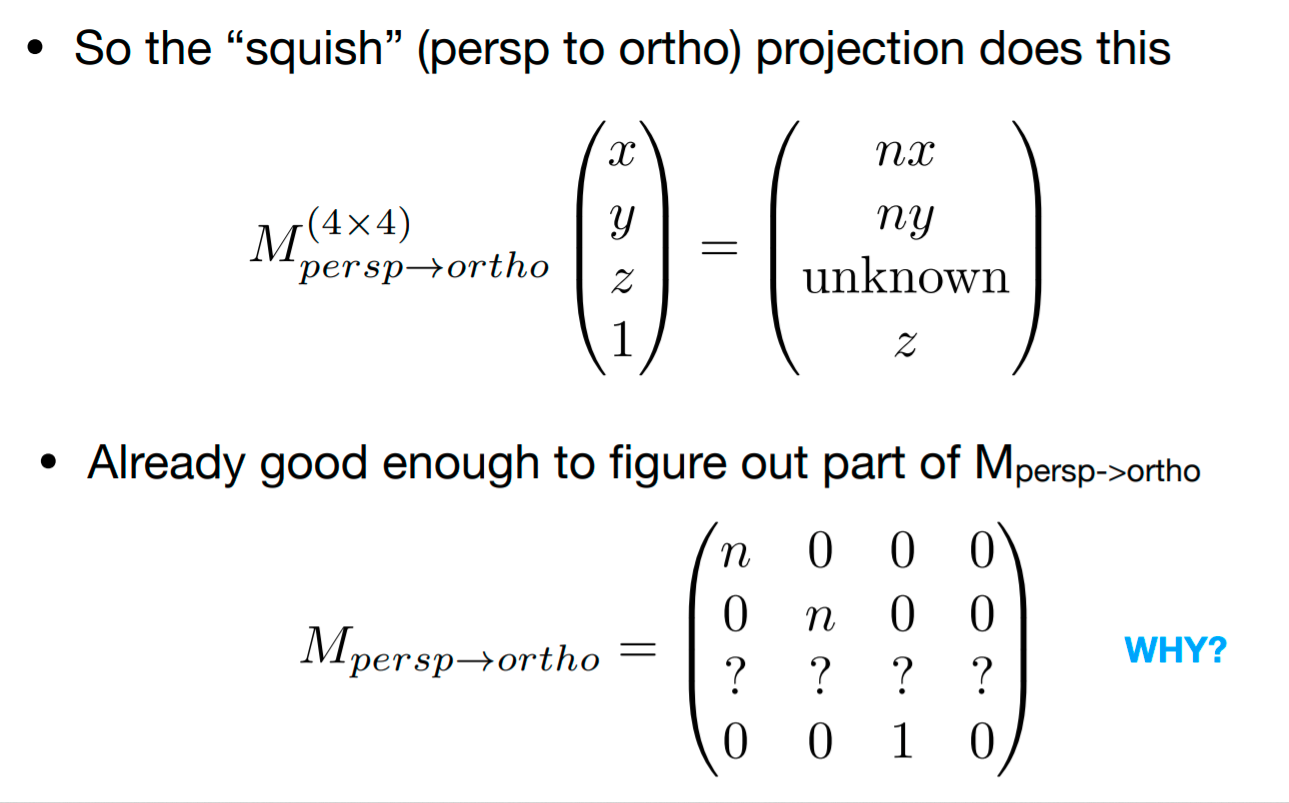
image-20210409201407603 image-20210409203702948 image-20210409212204189 image-20210409212443914

同理我们还可以找远平面上的特殊点

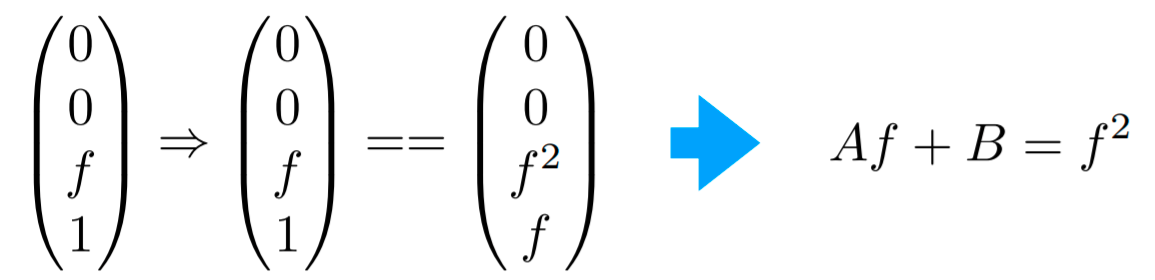
image-20210409213757960 image-20210409213954347

最后很有意思的一个问题，就是在两个平面之间的点的z坐标是怎么变化的呢？

答案是都变得更远了，数值上（因为是往-z方向，所以数值上都变得更小了。

即，从n到f的过程中，慢慢变得更远然后再慢慢回归不变