A. 越狱

题意： 给定一个长度为$nn$的序列$aa$，找到一个最小的正整数$xx$，使得最大化。 数据范围： $1\le n\le 2\times 10^5,1\le a_i\le 2\times 10^{9}1\backslash leq\; n\backslash leq\; 2\backslash times\; 10^5,1\backslash leq\; a\_i\backslash leq\; 2\backslash times\; 10^9$ 对于，都有

题解： 找到排名为$\frac{n}{2}\backslash frac\{n\}\{2\}$的数即可

代码：

#include<bits/stdc++.h>
using namespace std;

const int N = 100010;
int a[N], n;
int c[N];

int main()
{
    scanf("%d", &n);
    for(int i = 0; i < n; ++i) scanf("%d", &a[i]);
    nth_element(a, a + n / 2 - 1, a + n);
    printf("%d %d\n", n / 2, a[n / 2 - 1] + 1);
    return 0;
}

B. 物流

题意： A地有 $aa$ 吨货物，B地有 $bb$ 吨货物，C地需要 $cc$ 吨货物，D地需要 $dd$ 吨货物。$11$吨货物从A到C花 $acac$的代价，从A到D花 $adad$的代价，从B到C花 $bcbc$的代价，从B到D花 $bdbd$的代价。求最小代价。 注意，从A/B地到C/D地的货物是一吨一吨运输的，也就是说你可以选择A/B地的一部分货物来满足C/D地的一部分需求，但是最终C/D的需求必须全部满足。 输入只含有正整数。

数据范围： $TT$组数据，$1\le T\le 10^{5}1\backslash leq\; T\backslash leq\; 10^5$ $1\le a,b,c,d,ac,ad,bc,cd\le 2\times 10^{9}1\backslash leq\; a,b,c,d,ac,ad,bc,cd\backslash leq\; 2\backslash times\; 10^9$ $a+b=c+da+b=c+d$

题解： 考虑$ac,ad,bc,bdac,\; ad,\; bc,\; bd$ 如果$max(ac,ad)-min(ac,ad)>max(bc,bd)-min(bc,bd)max(ac,\; ad)\; -\; min(ac,\; ad)\; >\; max(bc,\; bd)\; -\; min(bc,\; bd)$ 那么必然是优先处理掉$min(ac,ad)min(ac,\; ad)$，这样使得少一点支出， 所以这里只需要考虑优先处理掉$ac,ad,bc,bdac,ad,bc,bd$中的一种即可。

代码：

#include<bits/stdc++.h>
using namespace std;

typedef long long ll;

void solve(int ca) {
	ll a, b, c, d, v[5];
	scanf("%lld%lld%lld%lld%lld%lld%lld%lld", &a, &b, &c, &d, &v[1], &v[2], &v[3], &v[4]);
	ll res = 9e18;
	// a -> c
	{
		if(a >= c) {
			res = min(res, c * v[1] + (a - c) * v[2] + b * v[4]); // a->c, a->d, b->d
		} else if(a < c) {
			res = min(res, a * v[1] + (c - a) * v[3] + d * v[4]); // a->c, b->c, b->d
		}
	}
	
	// a -> d
	{
		if(a >= d) {
			res = min(res, d * v[2] + (a - d) * v[1] + b * v[3]); // a->d, a->c, b->d
		} else if(a < d) {
			res = min(res, a * v[2] + (d - a) * v[4] + c * v[3]); // a->d, b->d, b->c
		}
	} 
	
	// b -> c
	{
		if(b >= c) {
			res = min(res, c * v[3] + (b - c) * v[4] + a * v[2]); // b->c, b->d, a->d
		} else if(b < c) {
			res = min(res, b * v[3] + (c - b) * v[1] + d * v[2]); // b->c, a->c, a->d
		}
	}
	
	// b -> d
	{
		if(b >= d) {
			res = min(res, d * v[4] + (b - d) * v[3] + a * v[1]); // b->d, b->c, a->c 
		} else if(b < d) {
			res = min(res, b * v[4] + (d - b) * v[2] + c * v[1]); // b->d, a->d, a->c 
		}
	}

	
	printf("%lld\n", res);
}

int main()
{
	int T = 1;
	scanf("%d", &T);
	for(int i = 1; i <= T; ++i) solve(i);

	return 0;
}

C. 数的和与积

题意： 给定一个 $nn$ ，请你将 $11$ 到 $nn$ 中的所有整数划分为两个集合，使得第一个集合里的数的积等于第二个集合里的数的和。 输出第一个集合的数。无解输出 $-1-1$。

数据范围： $TT$组数据，$1\le T\le 10^{5}1\backslash leq\; T\backslash leq\; 10^5$ $1\le n\le 10^{9}1\backslash leq\; n\backslash leq\; 10^9$

题解： 模拟几个样例可以发现： $n=2n=2$和$n=4n=4$时无解，$n=3n=3$时可以分为 sum组$1\mathrm{、}21、2$，mul组$33$ 从$n=5n=5$开始， 存在有：

5
mul: 1 2 4

6
mul: 1 2 6

7
mul: 1 3 6

8
mul: 1 3 8

9
mul: 1 4 8

10
mul: 1 4 10

11 
mul: 1 5 10

12
mul: 1 5 12

可以发现三个数字依次为：

• $11$
• $\lfloor \frac{n-1}{2}\rfloor \backslash lfloor\backslash frac\{n-1\}\{2\}\backslash rfloor$

证明： $(a+1)\times (b+1)=ab+a+b+1(a+1)\backslash times\; (b+1)=ab+a+b+1$ 移项：$(a+1)\times (b+1)-a-b-1=ab\times 1(a+1)\backslash times\; (b+1)-a-b-1=ab\backslash times\; 1$ 因此只要找到$aa$和$bb$满足$a+b+1+ab=\frac{n\times (n+1)}{2}a+b+1+ab=\backslash frac\{n\backslash times(n+1)\}\{2\}$

$\frac{n\times (n+1)}{2}\backslash frac\{n\backslash times(n+1)\}\{2\}$必然是一个整数， 当$nn$是偶数，$a+1=\frac{n}{2}a+1=\backslash frac\{n\}\{2\}$ 和 $b+1=n+1b+1=n+1$ $a=\frac{n}{2}-1a=\backslash frac\{n\}\{2\}-1$，$b=nb=n$

当$nn$是奇数，$a+1=\frac{n+1}{2}a+1=\backslash frac\{n+1\}\{2\}$ 和 $b+1=nb+1=n$ $a=\frac{n+1}{2}-1a=\backslash frac\{n+1\}\{2\}-1$，$b=n-1b=n-1$

综合起来就是

当$n=2n=2$时，$a=0,b=2a=0,b=2$，$a=0a=0$，显然不合法 当$n=4n=4$时，$a=1,b=4a=1,b=4$，因为本身就需要选择一个$11$，所以这也不合法 当$n=3n=3$时，$a=1,b=2a=1,b=2$，此时再选择一个$11$，这里就不合法了，但是可以只选择一个$33$，这里的情况不符合公式，需要特判。

代码：

#include<bits/stdc++.h>
using namespace std;

typedef long long ll;
int n;

void solve() {
	scanf("%d", &n);
	if(n == 2 || n == 4) {
		puts("-1");
		return ;
	}
	
	if(n == 3) {
		puts("1\n3");
		return ;
	}
	
	printf("3\n1 %d %d\n", (n - 1) / 2, (n % 2 ? n - 1 : n));
	
}

int main()
{
	int T = 1;
	scanf("%d", &T);
	for(int i = 1; i <= T; ++i) solve();

	return 0;
}

D. 礼物

题意： 给定一棵$nn$个点的树，确定一个根使得 ${\sum }_{i=1}^n{\sum }_{j=1}^{n}LCA(i,j)\backslash sum\backslash limits\_\{i=1\}^n\; \backslash sum\backslash limits\_\{j=1\}^n\; LCA(i,j)$ 最大。 题目保证答案唯一。 数据范围：$1\le n\le 10^{6}1\backslash leq\; n\backslash leq\; 10^6$

题解： 换根$dpdp$ 这里先考虑以$11$为根进行$dfsdfs$，求出这样的一棵有根树的子树大小。 考虑以$11$为根的有根树

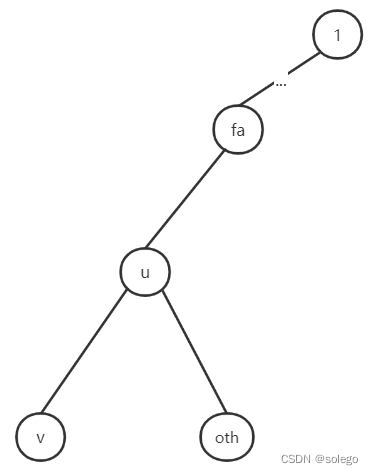
• $down[u]down[u]$表示$uu$的子树中的任意两点的LCA值之和
• $siz[u]siz[u]$表示$uu$的子树大小，包括$uu$
• 可以注意到的是树上任意一条边的两点$uu$和$vv$为根时，两者的${\sum }_{i=1}^n{\sum }_{j=1}^{n}LCA(i,j)\backslash sum\backslash limits\_\{i=1\}^n\; \backslash sum\backslash limits\_\{j=1\}^n\; LCA(i,j)$ 差别在于：
  • 以$uu$为根时，v及其子树 到u、oth子树、u的父亲fa对应的除去子树u的剩余子树对应的权值为：$siz[v]\times (n-siz[v])\times usiz[v]\backslash times\; (n-siz[v])\backslash times\; u$
  • 以$vv$为根时， u、oth子树、u的父亲fa对应的除去子树u的剩余子树到v及其子树对应的权值为：$siz[v]\times (n-siz[v])\times vsiz[v]\backslash times\; (n-siz[v])\backslash times\; v$ 两者的其余部分是完全相同的，分别为：
• $down[v]down[v]$
• $down[oth]down[oth]$
• $\sum _{son\in fa}[son\mathrm{\ne }u]down[son]\backslash sum\backslash limits\_\{son\; \backslash in\; fa\}\; [son\; \backslash ne\; u]down[son]$

代码：

#include<bits/stdc++.h>
using namespace std;

typedef long long ll;

const int N = 1000010;
const int M = N << 1;
int h[N], e[M], ne[M], idx;
int n, id;
ll sum, ans;
ll siz[N];

void add(int a, int b) {
	e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void dfs1(int u, int fa) {
	siz[u] = 1;
	for(int i = h[u]; i != -1; i = ne[i]) {
		int v = e[i];
		if(v != fa) {
			dfs1(v, u);
			sum += siz[u] * siz[v] * u;
			siz[u] += siz[v];
		}
	}
}

void dfs2(int u, int fa) {
	
	if(sum > ans) {
		ans = sum;
		id = u;
	}
	
	for(int i = h[u]; i != -1; i = ne[i]) {
		int v = e[i];
		if(v != fa) {
			ll temp = siz[v] * (n - siz[v]) * (u - v);
			sum -= temp;
			dfs2(v, u);
			sum += temp;
		}
	}
}

void solve(int ca) {
	scanf("%d", &n);
	memset(h, -1, (n + 1) * sizeof(int));
	idx = 0;
	
	for(int i = 1; i < n; ++i) {
		int a, b;
		scanf("%d%d", &a, &b);
		add(a, b);
		add(b, a);
	}
	
	dfs1(1, -1);
	ans = 0;
	dfs2(1, -1);
	
	printf("%d %lld\n", id, ans * 2 + 1ll * n * (n + 1) / 2);
}

int main()
{
	int T = 1;
//	scanf("%d", &T);
	for(int i = 1; i <= T; ++i) solve(i);

	return 0;
}