Glove公式推导_牛客博客

定义符号：
$X_{i} = <munderover> \sum j = 1 N </munderover> X_{i, j} P_{i, k} = \frac{X_{i, k}}{X_{i}} r a t i o_{i, j, k} = \frac{P_{i, k}}{P_{j, k}}$

ratio_i,j,k的值	单词j,k相关	单词j,k不相关
单词i,k相关	趋近1	很大
单词i,k不相关	很小	趋近1

推导：
假设已经得到词向量，则词向量和共现矩阵应该具有很好的一致性。假设词向量 $v_i ,v_j, v_k$ 计算 $r a t i o_{i, j, k}$ 的函数为 $g (w_{i}, w_{j}, w_{k})$ ,则：

$\frac{P_{i, k}}{P_{j, k}} = r a t i o_{i, j, k} = g (w_{i}, w_{j}, w_{k})$
需要等式左右尽可能接近，所以代价函数：
$J = <munderover> \sum i, j, k N </munderover> (\frac{P_{i, k}}{P_{j, k}} - g (w_{i}, w_{j}, w_{k}))^{2}$
但是模型包括三个单词，复杂度 $N * N * N$ 。
如何简化:

要考虑单词i和j之间的关系，则g大概会有 $w_{i} - w_{j}$ ;
$r a t i o_{i, j, k}$ 是标量，g也应该是标量，所以g应该包含 $(w_{i} - w_{j})^{T} w_{k}$ ;
再套上指数运算 $e x p ()$ ,最终 $g (w_{i}, w_{j}, w_{k}) = e x p ((w_{i} - w_{j})^{T} w_{k})$

$\frac{P_{i, k}}{P_{j, k}} = g (w_{i}, w_{j}, w_{k}) \frac{P_{i, k}}{P_{j, k}} = e x p ((w_{i} - w_{j})^{T} w_{k}) \frac{P_{i, k}}{P_{j, k}} = e x p (w_{i}^{T} w_{k} - w_{j}^{T} w_{k}) \frac{P_{i, k}}{P_{j, k}} = \frac{e x p (w_{i}^{T} w_{k})}{e x p (w_{j}^{T} w_{k})}$
可以看出：
$P_{i, j} = e x p (w_{i}^{T} w_{j})$ $l o g (X_{i, j}) - l o g (X_{i}) = w_{i}^{T} w_{j}$ $l o g (X_{i, j}) = w_{i}^{T} w_{j} + b_{i} + b_{j}$
损失函数变为：
$J = <munderover> \sum i, j N </munderover> (w_{i}^{T} w_{j} + b_{i} + b_{j} - l o g (X_{i, j}))^{2}$
矩阵分解方法，有个缺点，就是各个词的权重是一样的
基于出现频率越高的词对权重应该越大的原则，损失函数添加权重项：
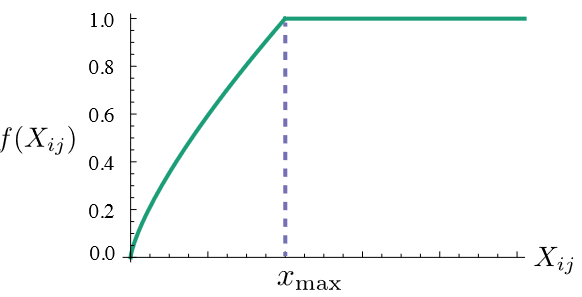
$J = <munderover> \sum i, j N </munderover> f (X_{i, j}) (v_{i}^{T} v_{j} + b_{i} + b_{j} - l o g (X_{i, j}))^{2}$ $f (x) = {\begin{matrix} <mstyle displaystyle="false" scriptlevel="0"> (x / x_{m a x})^{0.75}, </mstyle> & <mstyle displaystyle="false" scriptlevel="0"> <mtext> if </mtext> x < x_{m a x} </mstyle> \\ <mstyle displaystyle="false" scriptlevel="0"> 1, </mstyle> & <mstyle displaystyle="false" scriptlevel="0"> <mtext> if </mtext> x > = x_{m a x} </mstyle> \end{matrix}$