边缘
边缘(edge)是指图像局部强度变化最显著的部分。主要存在于目标与目标、目标与背景、区域与区域(包括不同色彩)之间,是图像分割、纹理特征和形状特征等图像分析的重要基础。
图像强度的显著变化可分为:
- 阶跃变化函数,即图像强度在不连续处的两边的像素灰度值有着显著的差异;
- 线条(屋顶)变化函数,即图像强度突然从一个值变化到另一个值,保持一较小行程后又回到原来的值。
图像的边缘有方向和幅度两个属性,沿边缘方向像素变化平缓,垂直于边缘方向像素变化剧烈.边缘上的这种变化可以用微分算子检测出来,通常用一阶或二阶导数来检测边缘。

(a)(b)分别是阶跃函数和屋顶函数的二维图像;(c)(d)是阶跃和屋顶函数的函数图象;(e)(f)对应一阶倒数;(g)(h)是二阶倒数。
Sobel算子
- 离散微分算子,用来计算图像灰度的近似梯度
- 功能集合高斯平滑和微分求导
- 又称为一阶微分算子,求导算子,在水平和垂直方向上求导,得到图像x方向和y方向的方向梯度图像
sobel算子的表示:

梯度幅值:
1.平方开方形式
2.

用卷积模板来实现:

//Sobel_x 计算横向的梯度, 应用:检验纵向边缘,计算法线的横向偏移;
//Sobel_y 计算纵向的梯度, 应用:检验横向边缘,计算法线的纵向偏移;
Mat h_kernel = (Mat_<int>(3, 3) << -1,0,1,-2,0,2,-1,0,1);
filter2D(src1,dst,-1,h_kernel,Point(-1,-1));
Mat z_kernel = (Mat_<int>(3, 3) << -1, -2, -1, 0, 0, 0, 1, 2, 1);
filter2D(src1, src2, -1, z_kernel, Point(-1, -1));
api
void Sobel(InputArray src, OutputArray dst, int ddepth, int dx, int dy, int ksize=3, double scale=1, double delta=0, int borderType=BORDER_DEFAULT ) 参数解释:
InputArray src:输入的原图像,Mat类型
OutputArray dst:输出的边缘检测结果图像,Mat型,大小与原图像相同。
int ddepth:输出图像的深度,针对不同的输入图像,输出目标图像有不同的深度,具体组合如下:
| src.depth() = CV_8U | ddepth =-1/CV_16S/CV_32F/CV_64F |
| src.depth() = CV_16U/CV_16S | ddepth =-1/CV_32F/CV_64F |
| src.depth() = CV_32F | ddepth =-1/CV_32F/CV_64F |
| src.depth() = CV_64F | ddepth = -1/CV_64F |
注:ddepth =-1时,代表输出图像与输入图像相同的深度。
int dx:int类型dx,x 方向上的差分阶数,1或0
int dy:int类型dy,y 方向上的差分阶数,1或0
其中,dx=1,dy=0,表示计算X方向的导数,检测出的是垂直方向上的边缘;dx=0,dy=1,表示计算Y方向的导数,检测出的是水平方向上的边缘。
int ksize:为进行边缘检测时的模板大小为ksize*ksize,取值为1、3、5和7,其中默认值为3。特殊情况:ksize=1时,采用的模板为3*1或1*3。
double scale:默认1。
double delta:默认0。
int borderType:默认值为BORDER_DEFAULT。
当ksize=3时,Sobel内核可能产生比较明显的误差,此时,可以使用 Scharr 函数,该函数仅作用于大小为3的内核。具有跟sobel一样的速度,但结果更精确,其内核为: 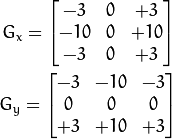
其调用格式为:
Scharr( src_gray, grad_x, ddepth, 1, 0, 1, 0, BORDER_DEFAULT );
Scharr( src_gray, grad_y, ddepth, 0, 1, 1, 0, BORDER_DEFAULT ); LapLace 拉普拉斯算子
拉普拉斯对噪声敏感,会产生双边效果。不能检测出边的方向。通常不直接用于边的检测,只起辅助的角色,检测一个像素是在边的亮的一边还是暗的一边利用零跨越,确定边的位置。
二维函数f(x,y)的拉普拉斯是一个二阶的微分,定义为:

其中:

可以用多种方式将其表示为数字形式。对于一个3*3的区域,经验上被推荐最多的形式是:

定义数字形式的拉普拉斯要求系数之和必为0

拉普拉斯是用二阶差分计算边缘的,看连续函数的情况下
在一阶微分图中极大值或极小值处,认为是边缘。
在二阶微分图中极大值和极小值之间的过 0 点,被认为是边缘。
拉普拉斯算子推导:
一阶差分:f '(x) = f(x) - f(x - 1)
二阶差分:f '(x) = (f(x + 1) - f(x)) - (f(x) - f(x - 1))
化简后:f '(x) = f(x - 1) - 2 f(x)) + f(x + 1)
提取前面的系数:[1, -2, 1]
二维的情况下,同理可得
f '(x, y) = -4 f(x, y) + f(x-1, y) + f(x+1, y) + f(x, y-1) + f(x, y+1)
提取各个系数,写成模板的形式
0, 1, 0
1, -4, 1
0, 1, 0
考虑两个斜对角的情况
1, 1, 1
1, -8, 1
1, 1, 1
这就是拉普拉斯算子,与原图卷积运算即可求出边缘。
//拉普拉斯算子
Mat lpls = (Mat_<int>(3,3) << 0,-1,0,-1,4,-1,0,-1,0);
filter2D(src1,src3,-1,lpls,Point(-1,-1)); API
CV_EXPORTS_W void Laplacian( InputArray src, OutputArray dst, int ddepth,
int ksize=1, double scale=1, double delta=0,
int borderType=BORDER_DEFAULT );
参数详解:
- src_gray,输入图像
- dst,Laplace操作结果
- ddepth,输出图像深度,因为输入图像一般为CV_8U,为了避免数据溢出,输出图像深度应该设置为CV_16S
- kernel_size,filter mask的规模,我们的mask时3x3的,所以这里应该设置为3
- scale,delta,BORDER_DEFAULT,默认设置就好
Sobel求边缘实例演示
- 高斯平滑
- 转灰度
- 求梯度x,y
- 综合
#include<iostream>
#include<opencv2/opencv.hpp>
using namespace std;
using namespace cv;
Mat src1, src2;
int main()
{
src1 = imread("C:\\Users\\马迎伟\\Desktop\\heibao.jpg");
if (src1.empty())
{
cout << "could not find src1" << endl;
return -1;
}
namedWindow("input", CV_WINDOW_AUTOSIZE);
imshow("input", src1);
//Sobel求边缘 : 高斯平滑-->转灰度-->求梯度x,y-->综合
GaussianBlur(src1,src2,Size(3,3),0,0);
Mat gray_img,xg,yg;
cvtColor(src2,gray_img,CV_BGR2GRAY);
imshow("gray image",gray_img);
//Sobel(gray_img,xg,CV_16S,1,0,3);
Scharr(gray_img, xg, CV_16S, 1, 0, 3);
//至关重要的一步,将负值绝对值,使得特征得以显示出来,否则会被置为0;
//应该是根号下平方相加 ---- 改成绝对值相加
convertScaleAbs(xg,xg);
imshow("xg",xg);
//Sobel(gray_img,yg,CV_16S,0,1,3);
Scharr(gray_img, yg, CV_16S, 0, 1, 3); //边缘提取较多
convertScaleAbs(yg, yg);
imshow("yg",yg);
//将 梯度按一定比例融合
//addWeighted(xg,0.5,yg,0.5,0,dst);
//效果比较好
Mat dst = Mat(gray_img.size(),gray_img.type());
printf("%d",dst.type());
for (int row = 0; row < src1.rows; row++)
{
for (int col = 0; col < src1.cols; col++)
{
int x = xg.at<uchar>(row, col);
int y = yg.at<uchar>(row, col);
dst.at<uchar>(row,col) = x + y; //类型不一样容易产生截断效应 0是8U_CHAR类型
}
}
imshow("output",dst);
waitKey(0);
return 0;
} Laplance算子实例
#include<iostream>
#include<opencv2/opencv.hpp>
using namespace std;
using namespace cv;
Mat src1, src2;
int main()
{
src1 = imread("C:\\Users\\马迎伟\\Desktop\\heibao.jpg");
if (src1.empty())
{
cout << "could not find src1" << endl;
return -1;
}
namedWindow("input", CV_WINDOW_AUTOSIZE);
imshow("input", src1);
//Laplacian求边缘 : 高斯平滑-->转灰度-->拉普拉斯求二阶梯度-->取绝对值
GaussianBlur(src1, src2, Size(3, 3), 0, 0);
Mat gray_img,abs,dst;
cvtColor(src2, gray_img, CV_BGR2GRAY);
imshow("gray image", gray_img);
Laplacian(gray_img, abs,CV_16S);
convertScaleAbs(abs,dst);
//取二值化,使结果表达更清晰
threshold(dst,dst,0,255,THRESH_OTSU | THRESH_BINARY);
imshow("output", dst);
waitKey(0);
return 0;
}




 京公网安备 11010502036488号
京公网安备 11010502036488号